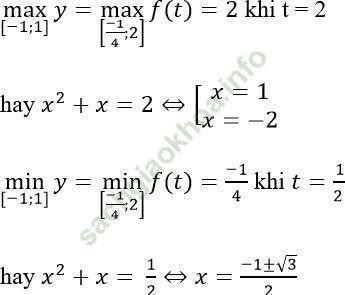Bài tập chương: Hàm số bậc nhất và bậc hai (Bài tập tự luận) - Chuyên đề Toán 10

Bài 1: Tìm tập xác định của các hàm số sau:

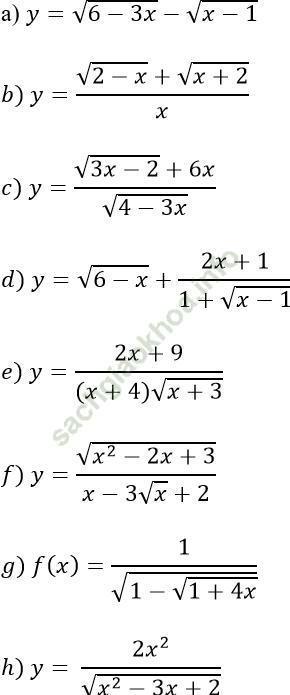
Bài giải:

a) Tập xác định: D = [1; 2]

b) Tập xác định: D = [-2; 2]\ {0}

c) Tập xác định: D = [2/3; 4/3)

d) Tập xác định: D = [1; 6]

e) ập xác định: D = (-3; +∞)

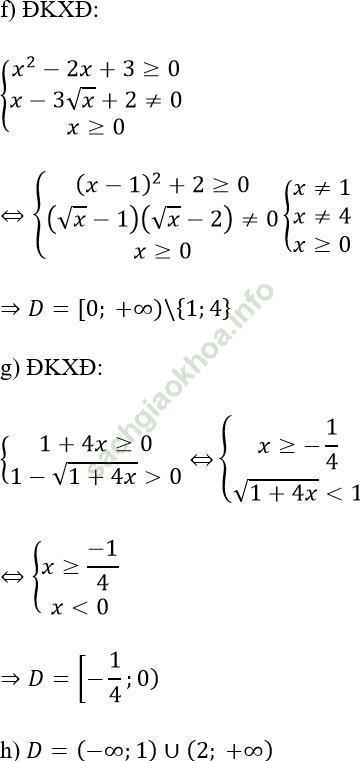
Bài 2: Xét tính chẵn, lẻ của các hàm số sau:

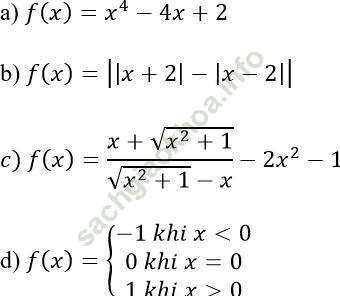
Bài giải:

a) f (x) = x⁴ - 4x + 2

TXĐ: D = R

Ta có: f (1) = -1; f (-1) = 7

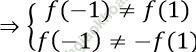
=> Hàm số không chẵn không lẻ.

b) f (x) = ||x + 2| - |x - 2||

TXĐ: D = R.

Với mọi x ∈ R ta có -x ∈ R, và:

f (-x) = ||-x + 2| - |-x - 2|| = ||x + 2| - |x - 2|| = f (x)

Vậy hàm số: f (x) = ||x + 2| - |x - 2|| là hàm số chẵn.

Vậy hàm số đã cho là hàm số lẻ.

d)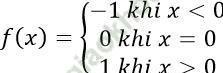

Ta có: TXĐ: D = R.

Dễ thấy mọi x ∈ R ta có -x ∈ R

Với mọi x > 0 ta có – x < 0 suy ra f (-x) = -1 ⇒ f (-x) = -f (x)

Với mọi x < 0 ta có – x > 0 suy ra f (-x) = 1 ⇒ f (-x) = -f (x)

Và f (-0) = -f (0) = 0.

Do đó với mọi x ∈ R ta có f (-x) = -f (x)

Vậy hàm số đã cho là hàm số lẻ.

Bài 3: Tìm m để hàm số: 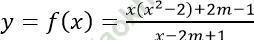là hàm số chẵn.

Bài giải:

Hàm số: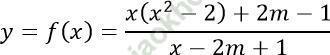

Hàm số xác định khi: x - 2m + 1 ≠ 0 ⇔ x ≠ 2m - 1

Hàm số đã cho là hàm số lẻ khi f (-x) = -f (x), ∀ x ∈ D

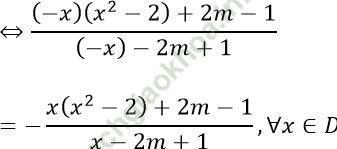
⇔ [(-x)(x² - 2) + 2m - 1](x - 2m + 1) = - [x (x² - 2) + 2m - 1]( (-x) - 2m + 1), ∀ x ∈ D

⇔ x⁴ = 2m (2m - 1), ∀ x ∈ D

⇔ 2m (2m - 1) = 0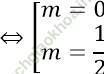

Với m = 0, hàm số trở thành: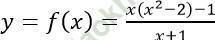

TXĐ: D = R\ {-1}

Ta có: x₀ = 1 ∈ D nhưng -x₀ = -1 ∉ D

Vậy hàm số đã cho không là hàm số lẻ.

Với m = 1/2, hàm số trở thành:

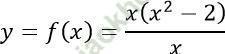
TXĐ: D = R \ {0}

Dễ thấy mọi x ∈ D ta có -x ∈ D

Vậy m = 1/2 là giá trị cần tìm.

Bài 4: Cho hàm số: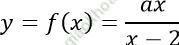

a) Với a = 1, khảo sát sự biến thiên của hàm số.

b) Tìm a để hàm số đồng biến trên (2; +∞)

Bài giải:

a) Với a = 1, hàm số trở thành: y = f (x) = x/ (x-2)

Hàm số xác định < => x-2≠ 0 < => x≠ 2

Vậy TXĐ: D = R\ {2}

Với x₁; x₂ ∈ D; x₁ ≠ x₂ ta có:

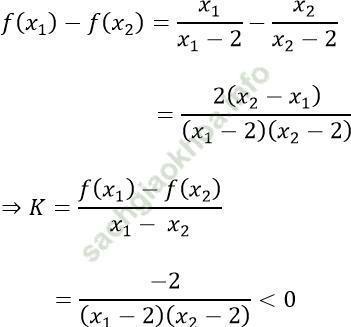
Do đó hàm số nghịch biến trên D.

b) TXĐ: D = R\ {2}

Với x₁; x₂ ∈ (2; +∞); x₁ ≠ x₂ ta có:

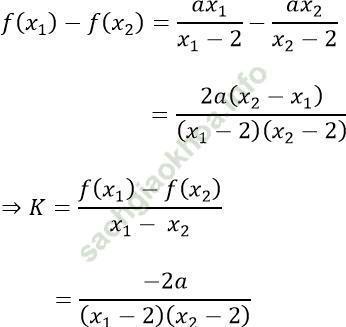
Hàm số đồng biến trên (2; +∞) khi K > 0.

⇔ -2a > 0 ⇔ a < 0

Vậy với a < 0 thì hàm số đồng biến trên (2; +∞).

Bài 5: Cho hàm số y = √ (x-1) + x² - 2x

a) Xét sự biến thiên của hàm số đã cho trên [1; +∞)

b) Tìm giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn [2; 5]

Bài giải:

a) TXĐ: D = [1; +∞)

Với x₁; x₂ ∈ D; x₁ ≠ x₂ ta có:

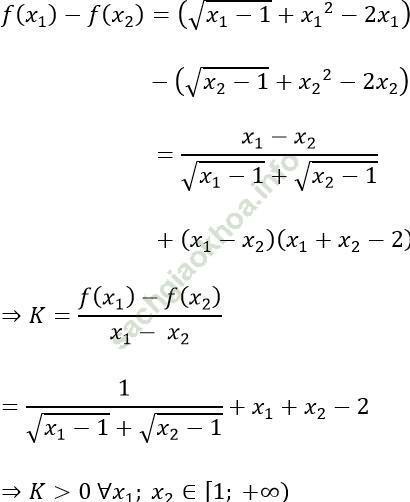
b) Do hàm số đồng biến trên đoạn [2; 5] nên ∀ x ∈ [2; 5] ta có:

f (2) ≤ f (x) ≤ f (5) ⇔ 1 ≤ f (x) ≤ 17

Vậy giá trị nhỏ nhất của hàm số trên [2; 5] là 1 khi x = 2.

Giá trị lớn nhất của hàm số trên [2; 5] là 17 khi x = 5.

Bài 6: Chứng minh rằng trên đồ thị (C) của hàm số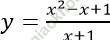tồn tại hai điểm A (x_A; y_A) và B (x_B; y_B) thỏa mãn: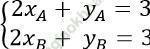

Bài giải:

Ta có:

Suy ra tồn tại hai điểm A (x_A; y_A) và B (x_B; y_B) thỏa mãn: 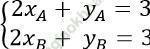(đpcm)

Bài 7: Cho hàm số y = ax + b

a) Xác định a, b biết rằng đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -4 và cắt trục hoành tại điểm có hoành độ bằng 1.

b) Vẽ đồ thị hàm số tìm được trong câu a)

c) Tính diện tích tam giác được tạo bởi đồ thị hàm số trong a) và các trục tọa độ.

Bài giải:

a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng – 4 => b = -4

Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 1 nên:

0 = a. 1 - 4 ⇒ a = 4

Vậy hàm số cần tìm là: y = 4x - 4.

b) Đồ thị hàm số y = 4x - 4 là đường thẳng đi qua hai điểm A (-4; 0) và B (1; 0)

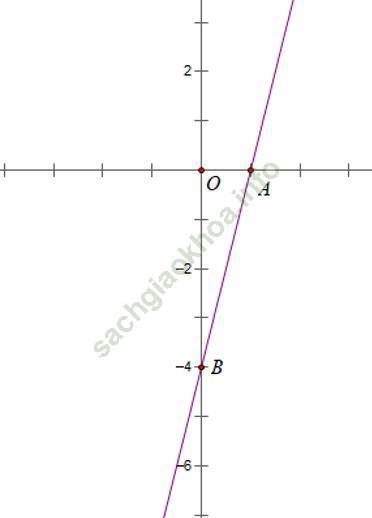
c) Gọi giao điểm của đồ thị hàm số với các trục Ox, Oy lần lượt là A, B

Ta có:

S_OAB = (1/2)OA. OB = (1/2).1.4 = 2

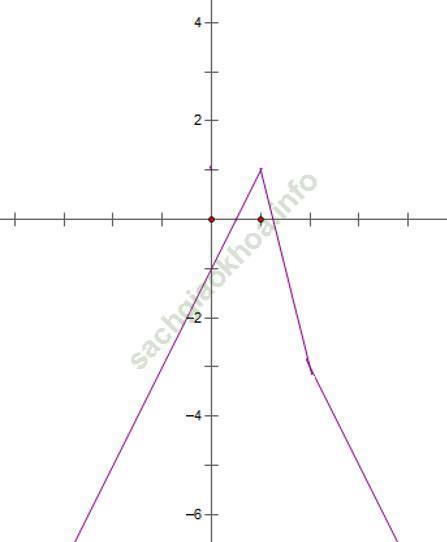
Bài 8: Lập bảng biến thiên và vẽ đồ thị của hàm số sau:

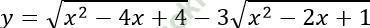
Từ đó tìm giá trị nhỏ nhất và lớn nhất của các hàm số đó trên [0; 2].

Bài giải:

Ta có:

Bảng biến thiên

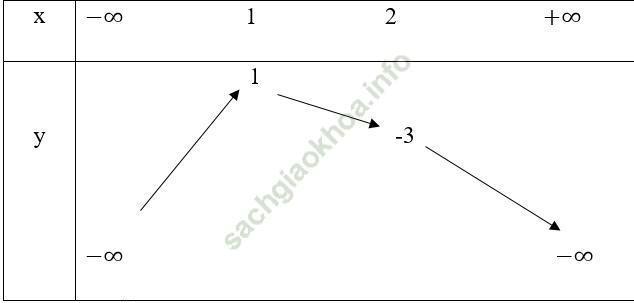
Từ bảng biến thiên ta có:

Bài 9: Cho các số thực không âm x, y, z thoả mãn x + y + z = 3.

Chứng minh rằng x² + y² + z² + xyz ≥ 4.

Bài giải:

Xét: x² + y² + z² + xyz ≥ 4

⇔ (y + z)² - 2yz + x² + xyz ≥ 4

⇔ (3 - x)² + x² + yz (x - 2) - 4 ≥ 0 (do x + y + z = 3)

⇔ yz (x - 2) + 2x² - 6x + 5 ≥ 0 (2)

Đặt t = yz, do yz ≥ 0 và yz ≤ ((y+z)/2)² = (3-x)²/4 nên t ∈ [0; (3-x)²/4]

Khi đó VT (2) là hàm số bậc nhất của biến t, f (t) = (x-2)t + 2x² - 6x + 5.

Để chứng minh bất đẳng thức (2) cần chứng minh:

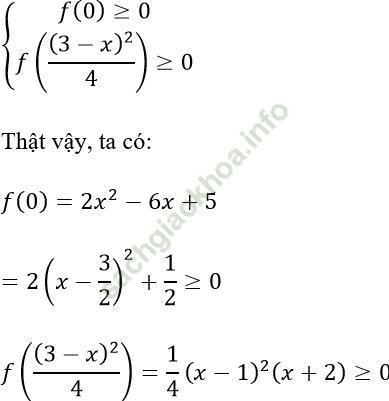
Đẳng thức xảy ra ⇔ x = y = z = 1.

Bài 10: Cho hàm số y = -1x²/2 - x + 3/2.

a) Lập bảng biến thiên và vẽ đồ thị các hàm số trên.

b) Dựa vào đồ thị trên, tùy theo giá trị của m, hãy cho biết số nghiệm của phương trình x² + 2x + 2m + 1 = 0.

c) Sử dụng đồ thị, hãy nêu các khoảng trên đó hàm số chỉ nhận giá trị âm.

Bài giải:

Bảng biến thiên

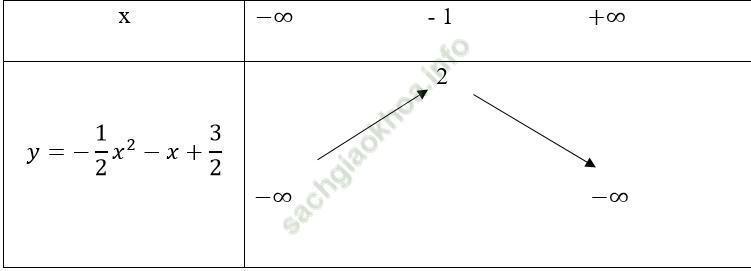
Từ bảng biến thiên suy ra đồ thị hàm số: y = -1x²/2 - x + 3/2 có đỉnh là I (-1; 2), đi qua các điểm A (0; 3/2) và B (1; 0), C (-3; 0).

Đồ thị hàm số nhận đường thẳng x = - 1 làm trục đối xứng và hướng bề lõm xuống dưới.

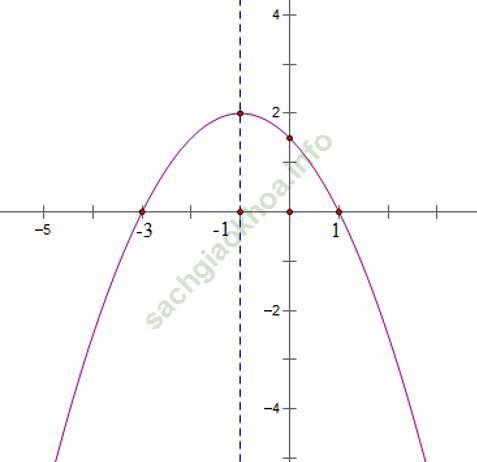
b) x² + 2x + 2m + 1 = 0

⇔ -1x²/2 - x + 3/2 = m - 1

Đường thẳng y = m – 1 song song hoặc trùng với trục hoành => Dựa vào đồ thị ta có:

Với m - 1 > 2 ⇔ m > 3 thì đường thẳng y = m – 1 và parabol

y = -1x²/2 - x + 3/2 không cắt nhau.

Với m - 1 = 2 ⇔ m = 3 thì đường thẳng y = m – 1 và parabol

y = -1x²/2 - x + 3/2 cắt nhau tại 1 điểm.

Với m - 1 < 2 ⇔ m < 3 thì đường thẳng y = m – 1 và parabol

y = -1x²/2 - x + 3/2 cắt nhau tại hai điểm phân biệt.

c) Hàm số nhận giá trị dương ứng với phần đồ thị nằm hoàn toàn trên trục hoành

=> Hàm số chỉ nhận giá trị âm khi và chỉ khi x ∈ (-∞; -3) ∪ (1; +∞).

d)

Bài 11: Tìm giá trị lớn nhất và nhỏ nhất của hàm số

a) y = x⁴ - 2x² trên [-2; 1].

b) y = x⁴ + 2x³ - x trên [-1; 1].

Bài giải:

a) y = x⁴ - 2x²

Đặt t = x², x ∈ [-2; 1] ⇒ t ∈ [0; 4]

Xét hàm số f (t) = t² - 2t, t ∈ [0; 4]

Ta có:

(-b)/ (2a) = 1; f (1) = -1; f (0) = 0; f (4) = 8

b) y = x⁴ + 2x³ - x = (x² + x)² - (x² + x)

Đặt t = x² + x.

Xét hàm số: t = x² + x với x ∈ [-1; 1]

Ta có -b/ (2a) = -1/2, bảng biến thiên là:

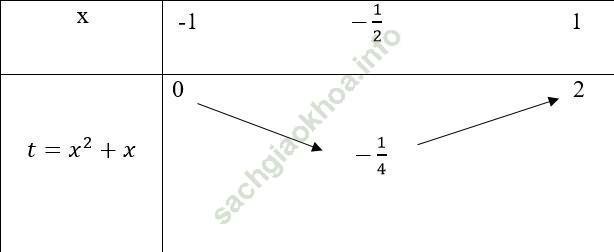
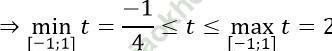
Khi đó, hàm số được viết lại: f (t) = t² - t với t ∈ [(-1)/4; 2].

Bảng biến thiên

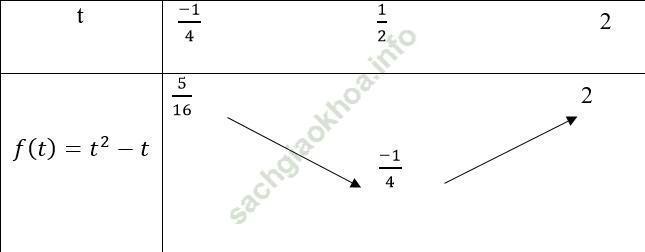
Từ bảng biến thiên ta có: