Ôn tập cuối năm (phần Đại số - phần Hình học) - trang 100 sách bài tập Toán 7 Tập 2
a) Tính các cạnh của tam giác Δ ABC;
b) Tam giác ABC có phải là tam giác vuông không? Vì sao?
Bài giải:a) Do các cạnh a, b, c tỉ lệ với 3; 4; 5 nên:
Mà chu vi tam giác ABC bằng 24 cm nên a+ b +c = 24
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
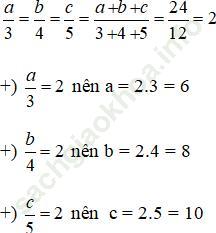
Vậy độ dài ba cạnh của tam giác ABC là 6cm, 8cm và 10cm.
b) Δ ABC là tam giác vuông vì a2 + b2 = 36 + 64 = 100 = c2.
Bài 6 trang 100: Trong mặt phẳng tọa độ hãy vẽ đường thẳng đi qua hai điểm O (0; 0) và A (1; 2). Đường thẳng OA là đồ thị của hàm số nào?
Bài giải: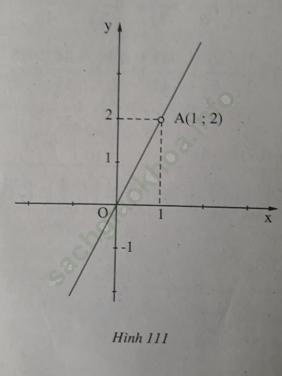
Trước hết hãy xác định các điểm O và A. O chính là gốc tọa độ. A là điểm có hoành độ là 1 và tung độ là 2. Xem hình 111.
+) Vì đường thẳng OA đi qua gốc tọa độ O nên OA là đồ thị của hàm số y = ax (a ≠ 0)
+) Vì đồ thị đi qua A (1; 2) nên thay x = 1; y = 2 vào ta được:
2 = a. 1 ⇔ a = 2
+) Vậy đường thẳng OA là đồ thị của hàm số y = 2x.
Bài 7 trang 100: Hàm số y = f (x) được cho bởi công thức y = -1,5 x.
a) Vẽ đồ thị của hàm số trên;
b) Bằng đồ thị hãy tìm các giá trị f (-2), f (1), f (2) (và kiểm tra lại bằng cách tính).
Bài giải:a) Vẽ hệ trục tọa độ Oxy
Với x= 2 ta được y = -3; điểm A (2; -3) thuộc đồ thị hàm số y = -1,5x.
Vậy đường thẳng OA là đồ thị của hàm số đã cho.
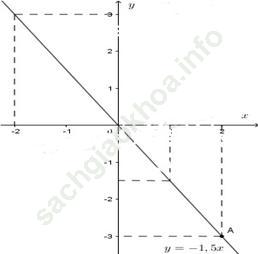
b)
+) Dựa vào đồ thị ta có:
f (-2) = 3; f (1) = -1,5 và f (2)= -3
+) Kiểm tra lại bằng phép tính:
f (-2) = - 1,5. (-2)= 3.
f (1) = -1,5.1 = -1,5
f (2) = -1,5.2 = - 3.
Bài 8 trang 100: Hãy sưu tầm một biểu đồ hình quạt (trong sách, báo hoặc tại một cuộc triển lãm) rồi nêu ý nghĩa của biểu đồ đó.
Bài giải:Học sinh tự sưu tầm.
Bài 9 trang 101: Hai vòi nước cùng chảy lần lượt vào hai bể. Bể thứ hai có sẵn 50 lít nước. Bể thứ nhất chưa có nước. Mỗi phút vòi thứ nhất chảy vào bể 1 được 20 lít, vòi thứ hai chảy vào bể 2 được 30 lít.
a) Viết biểu thức đại số mô tả số nước trong mỗi bể sau thời gian x phút.
b) Tính lượng nước có trong mỗi bể sau x = 1,2,3,10 phút rồi điền kết quả vào bảng sau:
 | 1 | 2 | 3 | 10 |
| Bể 1 | ||||
| Bể 2 | ||||
| Cả hai bể |
Bài giải:
a)
+) Sau x phút, bể 1 có 20. x (lít nước)
+) Vì bể thứ hai đã có sẵn 50 lít nước nên sau x phút thì bể thứ 2 có 50 + 30x (lít nước).
b)
 | 1 | 2 | 3 | 10 | 2 |
| Bể 1 | 20 | 40 | 60 | 200 | 20x |
| Bể 2 | 80 | 110 | 140 | 350 | 30x + 50 |
| Cả hai bể | 100 | 150 | 200 | 550 | 50x + 50 |
Bài 10 trang 101: Đánh dấu x vào ô mà em chọn là nghiệm của đa thức
1) 2x – 5
|
2,5 |
0 |
-2,5 |
2) 2x2 – 50
|
-5 |
-12,5 |
5 |
12,5 |
3) 13x – 26
|
-2 |
2 |
13 |
-13 |
4) -x2 + x + 2
|
-1 |
1 |
-2 |
2 |
Bài giải:
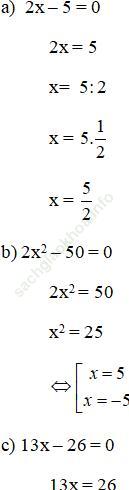
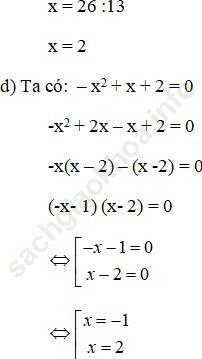
Bài 1 trang 101 sách bài tập Toán 7 Tập 2: Cho hình 107 trong đó ∠ B = 40o, ∠ D = 130o, AB // DE. Tính ∠ BCD.
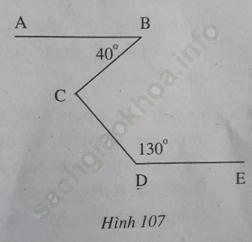
Bài giải:
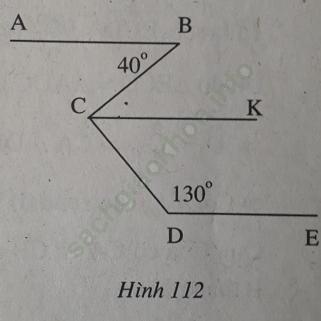
Kẻ CK // AB. Do CK // AB, DE // AB nên CK // DE.
AB // CK ⇒ ∠ BCK = ∠ B = 40° (so le trong)
CK // DE ⇒ ∠DCK + ∠CDE = 180° (hai góc trong cùng phía bù nhau)
⇒ ∠ DCK = 180° - ∠CDE = 180° - 130° = 50°.
Do đó: ∠ BCD = ∠ BCK + ∠ DCK = 40° + 50° = 90°.
Bài 2 trang 101: Cho góc vuông xOy, điểm A thuộc tia Ox, điểm B thuộc tia Oy. Gọi D, E theo thứ tự là trung điểm của OA, OB. Đường vuông góc với OA tại D và đường vuông góc với OB tại E cắt nhau ở C. Chứng minh rằng:
a) CE = OD; b) CE ⊥ CD;
c) CA = CB; d) CA // DE;
e) Ba điểm A, B, C thẳng hàng.
Bài giải: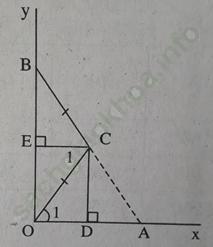
a) +) Vì CE // OD (cùng vuông góc với OB) ⇒ ∠ C1 = ∠ O1 (so le trong)
+) Xét ΔOCE và ΔCOD có:
OC chung
∠C1 = ∠O1 (chứng minh trên)
∠ OEC = ∠ ODC = 90º
Suy ra: Δ OCE = Δ COD (cạnh huyền – góc nhọn) ⇒ CE = OD.
b) CD // OE (cùng vuông góc OA) ⇒ ∠ (BEC) = ∠ (ECD) (so le trong)
Ta lại có ∠ (BEC) = 90o nên ∠ (ECD) = 90o.
Vậy CE ⊥ CD.
c) CD là đường trung trực của OA ⇒ CO = CA (tính chất đường trung trực) (1).
CE là đường trung trực của OB ⇒ CO = CB (tính chất đường trung trực) (2).
Từ (1) và (2) suy ra: CA = CB.
d) (h. 114) Ta có CE = OD (câu a))
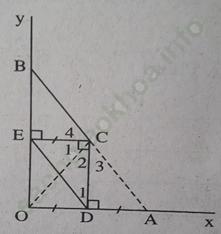
mà OD = DA (do D là trung điểm OA) nên CE = DA.
Xét ΔECD và ΔADC có:
CD chung
CE = DA (chứng minh trên)
∠ (ECD) = ∠ (CDA) = 90º
Do đó ΔECD = ΔADC (c. g. c)
⇒ ∠ D1 = ∠ C3 ⇒ CA // DE (hai góc so le trong bằng nhau).
e) Cách 1: Theo câu d): CA // DE. Chứng minh tương tự: CB // DE.
Qua C ta có CA và CB cùng song song với DE nên theo tiên đề Ơ-clit: A, C, B thẳng hàng.
Cách 2. CO = CA ⇒ Δ OCA cân ⇒ đường cao CD là đường phân giác của góc OCA ⇒ ∠ C2 = ∠ C3 ⇒ ∠ (OCA) = 2∠ C2.
Chứng minh tương tự: ∠ C1 = ∠ C4 ⇒ ∠ (OCB) = 2∠ C1.
Do đó:
∠ (OCA) + ∠ (OCB) = 2∠ C2 + 2∠ C1 = 2 (∠ C2 + ∠ C1) = 2∠ (ECD) = 2.90o = 180o.
Vậy A, C, B thẳng hàng.
Bài 3 trang 102: Tìm giá trị của x trên hình 108 biết rằng AB // DE
Bài giải: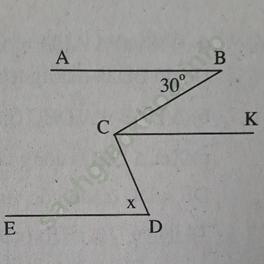
Kẻ CK // AB. Do CK // AB, DE // AB nên CK // DE.
Ta có AB // CK ⇒ ∠ (BCK) = ∠ B = 30o (so le trong)
Suy ra
∠ (DCK) = ∠ (BCD) - ∠ (BCK) = 100o - 30o = 70o.
CK // DE ⇒ ∠ D = ∠ (DCK) = 70o (so le trong)
Vậy x = 70o.
Bài 4 trang 102: So sánh các cạnh của tam giác CDE trên hình 109 biết rằng BE // CD.
Bài giải: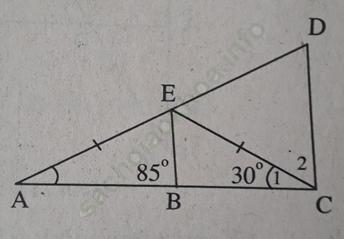
Trước hết ta tính các góc của Δ ECD.
Δ AEC cân tại E ⇒ ∠ A = ∠ C1 = 30o.
∠ (CED) là góc ngoài của Δ AEC tại đỉnh E.
⇒ ∠ (CED) = ∠ A + ∠ C1 = 30o + 30o = 60o.
BE // CD ⇒ ∠ (ACD) = ∠ (ABE) = 85o (đồng vị)
⇒ ∠ C2 = ∠ (ACD) - ∠ C1 = 85o - 30o = 55o.
Xét Δ ECD: ∠D + ∠ (CED) + ∠C2 = 180o (tổng ba góc của 1 tam giác).
Nên: ∠ D = 180o - ∠ (CED) - ∠ C2 = 180o - 60o - 55o = 65o.
Trong Δ ECD: ∠ C2 < ∠ (CED) < ∠ D ⇒ ED < CD < EC.
Bài 5 trang 102: Cho tam giác ABC vuông góc tại A, phân giác BD.
a) So sánh các độ dài AB và AD;
b) So sánh các độ dài BC và BD.
Bài giải: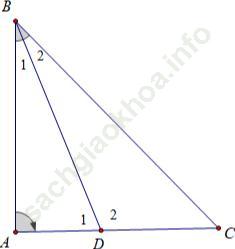
a)+) Xét tam giác BDC có ∠D1 là góc ngoài tam giác tại đỉnh D nên:
∠D1 = ∠B2 + ∠C
Suy ra: ∠ D1 > ∠ B2 (góc ngoài của Δ BDC)
Mà ∠ B1 = ∠ B2 (vì BD là tia phân giác của góc ABC) nên ∠ D1 > ∠ B1.
Δ ABD có ∠ D1 > ∠ B1 nên AB > AD.
b) Cách 1. Xét tam giác ABD có ∠D2 là góc ngoài tam giác tại đỉnh D nên:
∠D2 = ∠B1 + ∠A
Suy ra: ∠ D2 > ∠ A (góc ngoài của Δ ABD)
mà ∠ A = 90o nên ∠ D2 > 90o.
Δ BDC có ∠ D2 > 90o nên ∠ D2 > ∠ C, do đó BC > BD.
Cách 2. Xét các đường xiên BD, BC.
Đoạn thẳng AD; AC lần lượt là hình chiếu của BD; BC trên đường thẳng AC.
Hình chiếu AC > AD nên đường xiên BC > BD. ( quan hệ đường xiên và hình chiếu của chúng).
Bài 6 trang 102: Cho tam giác ABC vuông tại A, phân giác BD. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh rằng:
a) BD là đường thẳng trung trực của AE;
b) DF = DC;
c) AD < DC.
Bài giải: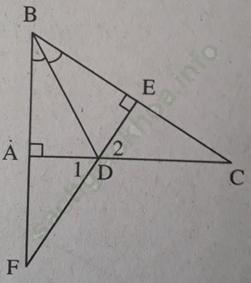
a) Xét ΔABD và ΔEBD có:
BD chung
∠ ABD = ∠ EBD (do BD, là tia phân giác của góc ABC)
∠ BAD = ∠ BED = 90º
Suy ra: Δ ABD = Δ EBD (cạnh huyền – góc nhọn) ⇒ BA = BE, DA = DE.
Do BA = BE nên B thuộc đường trung trực của AE.
Do DA = DE nên D thuộc đường trung trực của AE.
Do đó BD là đường trung trực của AE.
b) Xét ΔDAF và ΔDEC có:
DA = DE (chứng minh trên)
∠ D1 = ∠ D2 (hai góc đối đỉnh)
∠ DAF = ∠ DEC = 90º
Suy ra: ΔDAF = ΔDEC (g. c. g) ⇒ DF = DC.
c) Xét Δ DEC vuông tại E:
DE < DC (cạnh góc vuông nhỏ hơn cạnh huyền)
Ta lại có DA = DE (câu a)) nên DA < DC.
Bài 7 trang 102: a) Chứng minh rằng: Nếu tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC thì tam giác đo vuông tại A.
b) Ứng dụng: Một tờ giấy bị rách ở mép (h. 110). Hãy dùng thước và compa vẽ đường vuông góc với AB tại A.
Hướng dẫn: Vẽ điểm C sao cho CA = CB, rồi vẽ điểm E thuộc tia đối của tia CB sao cho CE = CB.
Bài giải: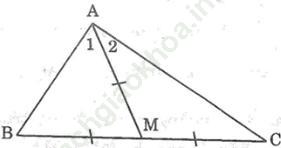
a) Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC
Mà AM = 1/2 BC (gt) nên: AM = BM = MC.
Tam giác AMB có AM = MB nên ΔAMB cân tại M
Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)
Tam giác AMC có AM = MC nên ΔAMC cân tại M
Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠ (BAC) (3)
Trong ΔABC ta có:
∠B + ∠C + ∠ (BAC) = 180o (tổng ba góc trong tam giác) (4)
Từ (3) và (4) suy ra: ∠ (BAC) + ∠ (BAC) = 180o ⇔ 2∠ (BAC) = 180o
Hay ∠ (BAC) = 90o.
Vậy ΔABC vuông tại A.
b) (h. 119) Δ ABE có đường trung tuyến AC bằng 1/2 BE nên ∠ (BAE) = 90o.
Vậy AE ⊥ AB.
Bài 8 trang 102: Cho tam giác ABC, đường cao AH. Vẽ điểm D sao cho AB là đường trung trực của HD. Vẽ điểm E sao cho AC là đường trung trực của HE. Gọi M, N theo thứ tự là giao điểm của DE với AB, AC. Xét xem các đường thẳng sau là các đường gì trong tam giác HMN: MB, NC, HA, HC, MC, từ đó hãy chứng minh rằng MC vuông góc với AB.
Bài giải: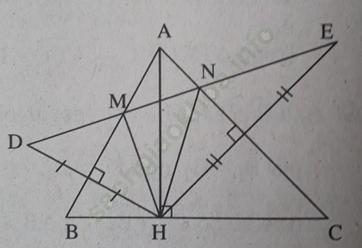
M thuộc đường trung trực của HD nên MH = MD. MB là đường trung trực của đáy HD của tam giác cân HMD nên MB là tia phân giác của góc HMD. Tương tự NC là tia phân giác của góc HNE. Vậy MB, NC là các đường phân giác góc ngoài của Δ HMN.
Các đường thẳng MB, NC cắt nhau tại A nên HA là đường phân giác trong của góc MHN của Δ HMN.
+) HC vuông góc với HA tại H mà HA là đường phân giác trong của góc MHN nên HC là đường phân giác góc ngoài của ΔHMN. ( đường phân giác góc trong và góc ngoài tại 1 đỉnh của 1 tam giác vuông góc với nhau)
+) Các đường thẳng HC và NC cắt nhau tại C; HC và NC là hai đường phân giác ngoài của tam giác HMN nên MC là đường phân giác góc trong của ΔHMN.
MB và MC là các tia phân giác của hai góc kề bù ∠ DMH; ∠ HMA nên MB ⊥ MC.
Vậy MC ⊥ AB.
Bài 9 trang 102: Tam giác ABC vuông tại A, đường cao AH, HC – HB = AB. Chứng minh rằng BC = 2AB.
Bài giải: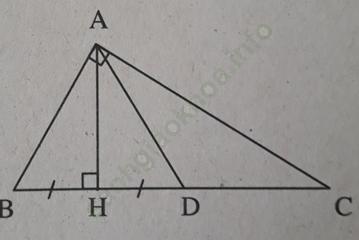
Trên HC lấy D sao cho HD = HB. Tam giác ABD có đường cao AH là trung tuyến nên là tam giác cân, suy ra
∠ (ADB) = ∠ B. (1)
Ta có: DC = HC – HD = HC – HB = AB = AD (vì tam giác ABD cân tại A)
Nên ΔADC cân tại D, do đó ∠ (DAC) = ∠C (2)
Ta có; ∠ADB + ∠DAC = ∠BAC = 90º (3)
Và ∠B + ∠C = 90º vì tam giác ABC vuông tại A (4)
Từ (2); (3) và (4) suy ra ∠ (DAB) = ∠B. (5)
Từ (1) và (5) suy ra ∠ (ADB) = ∠B = ∠ (DAB), do đó ΔABD là tam giác đều.
Suy ra AB = BD = AD = DC. Vậy BC = 2AB.