Bài 8: Tính chất ba đường phân giác của tam giác - trang 89 toán 7 VNEN tập 2

B. Hoạt động hình thành kiến thức

Câu hỏi trang 89 toán 7 VNEN tập 2.

Thực hiện các hoạt động sau

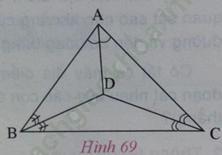
a) Ví dụ: Ở hình 69, D là giao điểm của ba đường phân giác, nó cách đền ba cạnh của tam giác này.

- Vẽ hình, viết giả thiết và kết luận cho tính chất trên.

b) Đọc và làm theo yêu cầu

- Giải bài toán sau:

Vẽ tam giác ABC. Gọi I là giao điểm của ba đường phân giác của tam giác đó. Kẻ IE, IF, IK lần lượt vuông góc với AB, BC, CA (E ∈ AB, F ∈ BC, K ∈ CA).

+ Điền dấu (> , < ,=) thích hợp vào chỗ trống (…): IE = IF…. IK.

+ Vẽ đường tròn tâm I bán kính IE. Quan sát hình vẽ, em có nhận xét gì về số điểm chung giữa đường tròn tâm I bán kính IE và ba cạnh của tam giác.

Bài giải:

- Giả thiết:

+) AM, BN, CF là các đường phân giác của tam giác ABC,

+) AM, BN, CF cắt nhau tại D

- Kết luận: Điểm D cách đều AB, AC, BC.

C. Hoạt động luyện tập

Câu hỏi trang 90 toán 7 VNEN tập 2.

a) Cho hình 70a.

- Chứng minh tam giác ABD bằng tam giác ACD;

- So sánh góc DBC và góc DCB.

b) Cho tam giác MNP. Vẽ hai đường phân giác MK và NH cắt nhau tại I. Cho góc NMP bằng 70 độ, góc MNP bằng 40 độ (h. 70b). Hãy tính số đo góc IPH.

Bài giải:

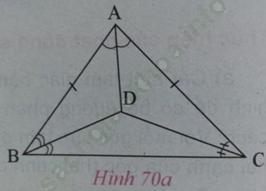
a)

- Chứng minh Δ ABD = Δ ACD

Xét hai Δ ABD và Δ ACD, có:

- AB = AC

- Góc DAB = góc DAC

- AD là cạnh chung

=> Δ ABD = Δ ACD (cạnh góc cạnh)

- So sánh góc DBC và góc DCB.

Theo cmt: Δ ABD = Δ ACD ⇒ Góc ABD = góc ACD (cặp góc tương ứng)

Mà theo giả thiết BD, CD lần lượt là phân giác của các góc ABC và ACB

=> góc DBC = góc DCB

b)

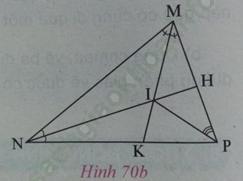
Trong tam giác MNP có NH và MK là hai đường phân giác cắt nhau tại I ⇒ PI cũng là đường phân giác của góc NPM trong tam giác MNP.

Theo gỉa thiết:

+) Góc NMP = 70 độ

+) Góc MNP = 40 độ

=> Góc NPM = 180 độ - (70 độ + 40 độ) = 70 độ

Do PI là phân giác của NPM ⇒ góc IPH = 1/2 góc NPM ⇒ góc IPH = 70 độ: 2 = 35 độ

D. E. Hoạt động vận dụng và tìm tòi mở rộng

Câu 1. trang 90 toán 7 VNEN tập 2.

Có hai con đường cắt nhau và cùng cắt một con sông tại 2 điểm khác nhau (h. 71).

Hãy tìm một địa điểm để xây dựng một đài quan sát sao cho khoảng cách từ đó đến hai con đường và đến bờ sông bằng nhau.

Có tất cả mấy địa điểm như vậy (cho rằng đoạn cắt nhau của các con đường và con sông là thẳng)?

Bài giải:

- Xác định 3 đường phân giác của 3 góc trong tam giác được tạo bởi 2 con đường và dòng sông cắt nhau. ⇒ Giao điểm của 3 đường phân giác đó là đọa điểm phù hợp để xay dựng đài quan sát đạt yêu cầu.

- Chỉ có duy nhất một điểm như trên.

Câu 3. trang 91.

Cho Δ ABC có góc A = 70 độ, các đường phân giác BD và CE cắt nhau tại I, Tính số đo góc BIC.

Bài giải:

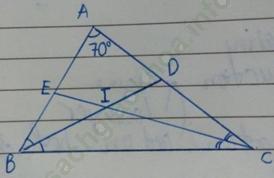
Ta có:

⇒ = 180⁰ - = 180⁰ - 70⁰ = 110⁰

Vì BD cà CE là 2 đường phân giác của và nên ta có:

⇒ = 180⁰ - =180⁰ - 55⁰ = 125⁰

Vậy = 125⁰

Câu 4. trang 91.

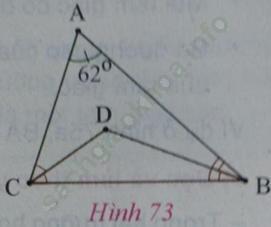
Trong hình 73, tam giác ABC có góc A bằng 62 độ; CD, BD lần lượt là đường phân giác ứng với các góc ACB và ABC.

a) Tính số đo của góc CDB.

b) Kẻ tia AD, tính số đo của góc CAD.

c) Điêm D có cách đều ba cạnh của tam giác ABC không? Tại sao?

Bài giải:

a) Ta có:

⇒ = 180⁰ - = 180⁰ - 62⁰ = 118⁰

Vì BD và CD là 2 đường phân giác của và nên ta có:

= . 118⁰ = 59⁰

⇒ = 180⁰ -

= 180⁰ - 59⁰ = 121⁰

Vậy = 121⁰

b) Trong tam giác ABC có 2 đường phân giác là BD và CD cắt nhau tại D ⇒ AD cũng là đường phân giác của góc CAB (theo tính chất đường phân giác trong tam giác).

Suy ra:

Vậy = 31⁰

c) Điểm D sẽ cách đều 3 cạnh của tam giác ABC. Vì theo tính chất đường phân giác của tam giác thì D là giao của 3 đường phân giác trong tam giác ABC nên nó cách đều 3 cạnh AB, AC và BC.

Bài trước: Bài 7: Tính chất tia phân giác của một góc, đường phân giác của tam giác - trang 85 toán 7 VNEN tập 2 Bài tiếp: Bài 9: Tính chất ba đường cao của tam giác - trang 91 toán 7 VNEN tập 2