Bài 3: Quan hệ giữa đường vuông góc và đường xiên, quan hệ giữa đường xiên và hình chiếu của nó - trang 69 toán 7 VNEN tập 2
Câu 1. trang 69 toán 7 VNEN tập 2. Thực hiện các hoạt động sau để hiểu thêm về hình chiếu
a) b) (Sgk)
c) Đọc và làm theo yêu cầu
Vẽ một đường thẳng a.
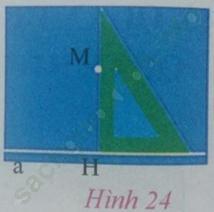
Vẽ một điểm M không thuộc a (h. 24).
Dùng êke để tìm hình chiếu H của điểm M trên a.
Sau đó vẽ đường vuông góc MH, đường xiên MK.
So sánh MH và MK?
Bài giải:
Trên đường thẳng a, lây K thuộc a (không trùng H) ta sẽ có tam giác MHK vuông tại K.
Xét tam giác vuông MHK có:
+ MK đối diện với góc H (= 90 độ)
+ MH đối diện với góc K (< 90 độ)
Suy ra ta luôn có MK > MH (cạnh đối diện với góc lớn hơn thì lớn hơn).
Câu 2. trang 70.
Thực hiện các hoạt động sau để hiểu thêm về đường vuông góc
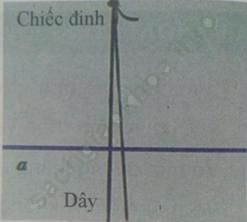
a, Quan sát và làm theo
Xác định xem với vị trí nào của dây thì khoảng cách từ giao điểm của dây và đường thẳng tới chiếc đinh là ngắn nhất?
b) Đọc và làm theo yêu cầu (Sgk)
c) Đọc kĩ nội dung sau (Sgk)
d) Đọc và làm theo yêu cầu
- Cho hình chữ nhật ABCD, các đường chéo là AC và BD (h. 27). Khi đó, BC vuông góc với CD nên C là hình chiếu của B trên CD, còn CD là hình chiếu của đường xiên DB trên CD, nên CD < DB.
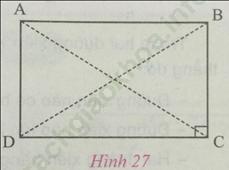
- So sánh AB và BD.
- So sánh AD và AC
- Xác định khoảng cách từ điểm D đến đường thẳng BC.
Bài giải:
a) Ở vị trí mà dây vuông góc với đường thẳng thì giao điểm của dây và đường thẳng tới đinh sẽ ngắn nhất.
Câu 3. trang 71.
a) Đọc và làm theo yêu cầu
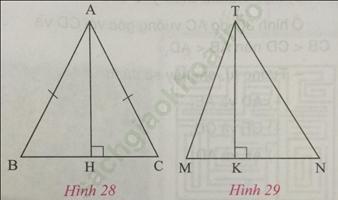
* Xem hình 28.
- Dùng thước đo và so sánh BH và HC.
- Nếu AB = AC thì có thể suy ra HB = HC hay không?
* Xem hình 29.
- Dùng thước đo độ dài các đoạn thẳng TM, TN, MK, KN. So sánh TM và TN. So sánh MK và NK.
- Nếu TM < TN thì có thể suy ra MK < KN hay không?
b) c) Sgk trang 72
d) Đọc và làm theo yêu cầu
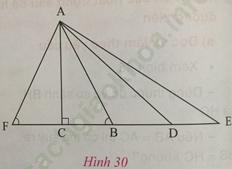
Ở hình 30, do AC vuông góc với CD và CB < CD nên AB < AD.
- Tương tự, em hãy so sánh:
+) AD và AE
+) CF và CD
+) AF và AD
C. Hoạt động luyện tậpCâu 1. trang 72 toán 7 VNEN tập 2.
a) Tìm một cách chứng minh khác của định lý ở phần c) trang này.
b)
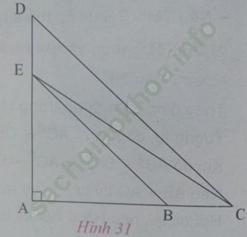
Xem hình 31, có BE ⁄ ⁄ CD và AD vuông góc với AC.
Chứng minh rằng:
+) BE < CE;
+) CE < CD;
+) BE < CD.
Bài giải:
a)
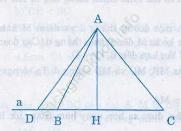
Từ điểm A nằm ngoài đường thẳng a, hạ đường vuông góc và cắt a tại H.
Lần lượt lấy D, C thuộc a sao cho H là trung điểm của DC. Lấy B bất kỳ sao cho B nằm giữa D và H (như hình trên). Ta có:
+ AB đối diện với góc vuông H, mà AD lại đối diện với góc tù B ⇒ AD > AB (cạnh đối diện với góc lớn hơn thì lớn hơn) (1)
+ Theo giả thiết, DH và BH lần lượt là hình chiếu của AD và AB lên a. DH > DB (theo hình vẽ) (2)
Từ (1) và (2) suy ra đường xiên nào lớn hơn thì có hình chiếu lớn hơn và đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Xét 2 tam giác vuông ADH và ACH có:
+ AH chung
+ 
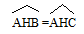(= 90 độ)
+ HD = HC (H là trung điểm của DC) (3)
Suy ra 
ADH = 
ACH ⇒ AD = AC (cặp cạnh tương ứng). (4)
HD và HC lần lượt là hình chiếu của AD và AC lên a. (5)
Từ (3), (4) và (5) suy ra Hai đường xiên bằng nhau thì có hình chiếu bằng nhau và hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
b) - Trong 
AEC có:
+ AB là hình chiếu của BE
+ AC là hình chiếu của CE
+ AB < AC (gt)
Suy ra BE < CE
- Trong 
AEC có:
+ AD là hình chiếu của DC
+ AE là hình chiếu của CE
+ AD > AE (gt)
Suy ra CD > CE
- Do BE < CE và CE < CD (chứng minh trên) ⇒ BE < CD
Câu 2. trang 73. Xem hình 32. Giải thích tại sao AD < BC
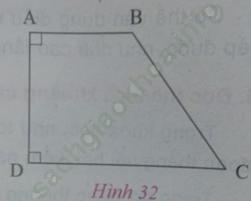
Bài giải:
- Từ B kẻ đường vuông góc với DC, cắt DC tại H. Khi đó, AD song song và bằng BH. (1)
Trong 
BHC có: BC > BH (BC là đường xiên) (2)
Từ (1) và (2) suy ra AD < BC.
D. E. Hoạt động vận dụng và tìm tòi mở rộngCâu 1. trang 73 toán 7 VNEN tập 2.
a) Một người tập đi trên khoảnh sân có dạng hình chữ nhật (h. 33). Hôm đầu người đó đi theo đoạn thẳng MA, hôm sau đi theo đoạn thẳng MB, hôm tiếp theo đi theo đoạn thẳng MC rồi đến MD. Theo cách đó thì ở lần tập đi sau người đó đi được xa hơn lần đi trước hay không? Vì sao?
b) Nếu một người đi ngang qua đường (h. 34), thì cách đi nào ngắn nhất? Giải thích theo cách hiểu của em?
c) Hình 35 thể hiện một mê cung, có cửa vào là A. Con đường nào là ngắn nhất để đi từ vị trí A đến vị trí B như trên?
Bài giải:
a) Theo hình vẽ các điểm A, B, C, D nằm trên một đường thẳng d và điểm M nằm ngoài đường thẳng đó. MA là đường vuông góc kẻ từ M đến đường thẳng d. Các đoạn thẳng MB, MC, MD là các đường xiên kẻ từ M lần lượt đến B, C và D
Ta có AB, AC, AD lần lượt là hình chiếu của MB, MC, MD xuống d. Ta có ngay AD > AC > AB suy ra MD > MC > MB > MA
Điều đó có nghĩa là ở lần tập đi sau người đó đi được xa hơn lần đi trước.
b) Người đó nên đi theo vạch kẻ dành cho người đi bộ. Vì khoảng cách từ bên này sang bên kia đường thông thường là khoảng cách của 2 đường thẳng song song, vạch kẻ được thiết kế như đường vuông góc và tạo ra khoảng cách ngắn nhất giữa 2 bên đường.
Câu 2. trang 73.
Buổi sáng, vào lúc trời có nắng, một người đặt một con thỏ bông trên sân, chiều cao của nó vuông góc với mặt sân, bóng của nó đổ dài trên sân (h. 36). Khi tia nắng tạo với mặt đất góc bao nhiêu độ thì chiều dài bóng của thỏ bông:
- dài hơn chiều cao của nó?
- bằng chiều cao của nó?
- ngắn hơn chiều cao của nó?
Bài giải:
- Khi tia nắng tạo với mặt đất góc nhỏ hơn 45 độ thì chiều dài bóng của thỏ bông dài hơn chiều cao của nó.
- Khi tia nắng tạo với mặt đất góc 45 độ thì chiều dài bóng của thỏ bông bằng chiều cao của nó.
- Khi tia nắng tạo với mặt đất góc lớn hơn 45 độ thì chiều dài bóng của thỏ bông ngắn hơn chiều cao của nó.
Bài trước: Bài 2: Quan hệ giữa ba cạnh của một tam giác - trang 66 toán 7 VNEN tập 2 Bài tiếp: Bài 4: Đường trung tuyến của tam giác, tính chất ba đường trung tuyến của tam giác - trang 76 toán 7 VNEN tập 2