Toán 7 VNEN Bài 6: Định lý Py-ta-go - trang 135
Vẽ một tam giác vuông có cạnh góc vuông bằng 3 cm, 4 cm (h. 105). Đo độ dài cạnh huyền của tam giác này và so sánh tổng các bình phương độ dài hai cạnh góc vuông với bình phương hai cạnh huyền
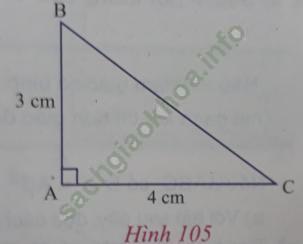
Trả lời:
Đo cạnh BC = 5cm
So sánh:
Câu 1 trang 135 toán 7 VNEN tập 1. Đọc kĩ nội dung sau (Sgk)
Câu 2 trang 135.
a) Quan sát hình 107 và đọc lời giải sau để tính độ dài cạnh AB: (sgk trang 135)
b) Tìm độ dài x trong mỗi trường hợp ở hình 108 và ghi vào vở.
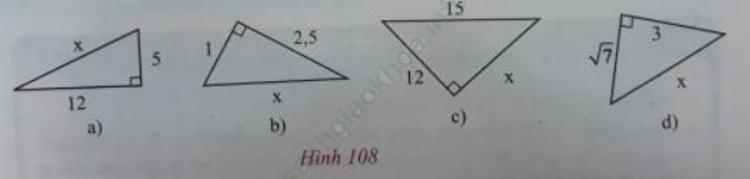
Trả lời:
b) Các tam giác ở hình 108 đều là tam giác vuông, áp dụng định lý Py-ta-go vào mỗi tam giác để tìm x như sau:
- Ở hình 108a: 122 + 52 = x2 ⇒ x2 = 169 ⇒ x= 13.
- Ở hình 108b: 12 + 2,52 = x2 ⇒ x2 = 7,25 ⇒ x = ![]()
- Ở hình 108c: 122 + x2 = 152 ⇒ x2 = 152 − 122 = 81 ⇒ x = 9.
- Ở hình 108d: ![]() + 32 = x2 ⇒ x2 = 16 ⇒ x = 4.
+ 32 = x2 ⇒ x2 = 16 ⇒ x = 4.
Câu 3 trang 136
Vẽ tam giác ABC có AB = 3 cm; AC = 5 cm; BC = 4 cm. Hãy dùng thước đo số đo góc ABC. Kiểm tra xem △ABC là tam giác gì?
Trả lời:
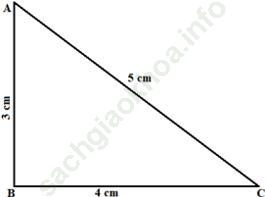
- Dùng thước đo góc đo số đo góc ABC, ta được:
- △ABC là tam giác vuông vì có ![]()
Câu 4 trang 136.
a) Đọc kĩ nội dung sau (Sgk trang 136)
b) Với bài sau đây, đọc cách trình bày câu i) và sau đó làm tiếp các câu ii), iii) vào vở. Trong các tam giác có độ dài ba cạnh như sau, tam giác nào là tam giác vuông?
i) 9 cm, 15 cm, 12 cm;
ii) 5 dm, 13 dm, 12 dm;
iii) 7 m, 7 m, 10 m;
Hướng dẫn, với câu i): Ta có: 152 = 225 và 92 + 122 = 81+144 = 225
⇒ 152 = 92 +122. Vậy các độ dài 9 cm, 15 cm, 12 cm là độ dài ba cạnh của một tam giác vuông (Định lý Py-ta-go đảo).
c) Bài toán: “Cho tam giác ABC có AB = 8, AC = 17, BC = 15. Tam giác ABC có phải là tam giác vuông hay không? ”. Bạn Tâm đã giải bài toán đó như sau:
“AB2 + AC2 = 82 + 172 = 64 + 289 = 353
BC2 = 152 = 225.
Do 353 ≠ 225 nên AB2+AC2≠BC2.
Vậy ABC không phải là tam giác vuông”.
Lời giải của bạn Tâm như trên đúng hay sai? Nếu sai hãy sửa lại cho đúng.
Trả lời:
b)
ii) Ta có: 132 = 169 và 52 + 122 = 25 + 144 = 169
⇒ 132 = 52 + 122. Vậy các độ dài 5 dm, 13 dm, 12 dm là độ dài ba cạnh của một tam giác vuông (Định lý Py-ta-go đảo).
iii) Ta có: 102 = 100 và 72 + 72 = 49 + 49 = 98
⇒ 102 ≠ 72 + 72. Vậy các độ dài 7 m, 7 m, 10 m không là độ dài ba cạnh của một tam giác vuông.
c) Lời giải của bạn Tâm như trên là sai.
Sửa lại:
“AB2 + BC2 = 82 + 1522 = 64 + 225 = 289
AC2 = 172 = 289.
Do 289 = 289 nên AB2 + BC2 = AC2.
Vậy ABC là tam giác vuông tại B”.
C. Hoạt động luyện tậpCâu 1 trang 136. Đoạn lên dốc từ C đến A dài 8,5 m, độ dài CB = 7,5 m (h. 109). Tính chiều cao AB.
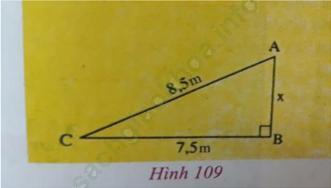
Trả lời:
△ABC vuông tại B.
Áp dụng định lí Py-ta-go, ta có: AB2 +BC2 = AC2 ⇒ AB = ![]() = 4 (m).
= 4 (m).
Câu 2 trang 137. Tính chiều cao của bức tường (h. 110), biết rằng chiều dài của thang là 4 m và chân thang cách tường là 1 m.
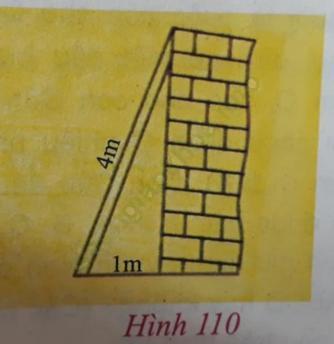
Trả lời:
Theo hình ta thấy thang, tường và mặt sàn tạo thành một tam giác vuông.
Áp dụng định lí Py-ta-go, ta có:
Chiều cao của tường là: h2 = 42 – 12
Câu 3 trang 137. Nếu ta đóng một nẹp chéo AC thì chiếc khung hình chữ nhật ABCD được vững hơn (h. 111). Tính độ dài AC, biết rằng AD = 40 cm, CD = 30.
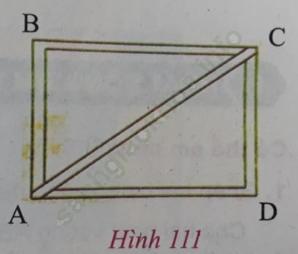
Trả lời:
△ADC vuông tại D nên áp dụng định lý Py-ta-go, ta có:
AC2 = AD2 + DC2 = 402 + 302 = 2500 ⇒ AC = 50 (cm).
Câu 4 trang 137. Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC (H thuộc BC). Cho biết AB = 14 cm, AH = 9 cm, HC = 12 cm. Tính các độ dài AC, BH.
Trả lời:
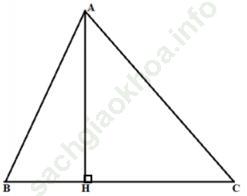
Xét tam giác AHC vuông tại H, theo định lí Pitago ta có
AC2 = AH2 + HC2 = 92 + 122 = 225 ⇒ AC = 15 (cm).
Xét tam giác ABH vuông tại H, ta có:
BH2 = AB2 – AH2 = 142 – 92 = 115 ⇒ BH = ![]() (cm)
(cm)
Câu 1 trang 137. Đố: Trong lúc anh Nam dựng cho tủ đứng thẳng, tủ có bị vướng vào trần nhà không? (h. 112)
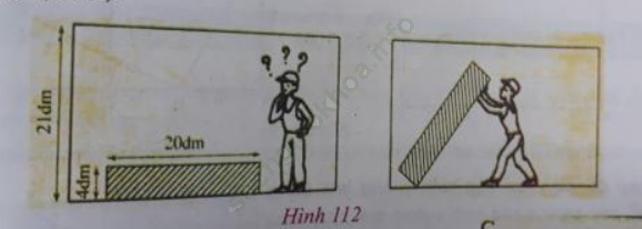
Trả lời:
Tủ không bị vướng vào trần nhà khi đường chéo của tủ nhỏ hơn chiều cao của nhà.
Đường chéo của tủ là: d = ![]() = 20,396 (dm) < 21 dm.
= 20,396 (dm) < 21 dm.
=> Tủ không bị vướng vào trần nhà.
Câu 2 trang 137. Trên giấy kẻ ô vuông (độ dài cạnh ô vuông bằng 1), cho tam giác ABC như hình 113. Tính độ dài mỗi cạnh của tam giác ABC.
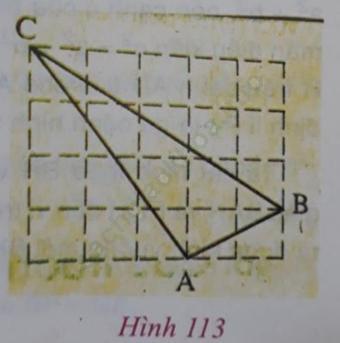
Trả lời:
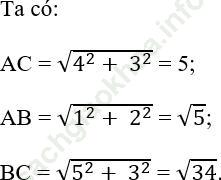
Câu 3 trang 138.
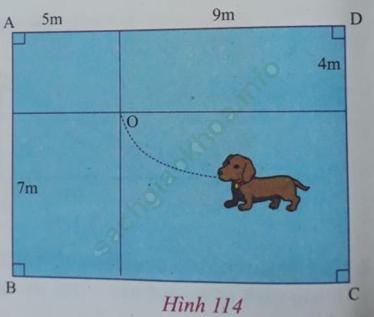
Đố: Người ta buộc con chó Cún bằng sợi dây, có một đầu buộc tại điểm O, sao cho con Cún di chuyển cách điểm O nhiều nhất là 10 m (h. 114). Con Cún có thể tới được các vị trí A, B, C, D để canh giữ mảnh vườn hình chữ nhật ABCD hay không? (Các kích thước như trên hình vẽ).
Trả lời:
Con Cún tới được các vị trí A, B, C, D khi OA, OB, OC, OD < 10 m.
Tính các đoạn OA, OB, OC, OD:
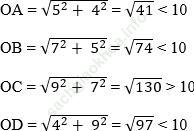
Vậy con cún chỉ có thể tới được các điểm A, B, D để canh giữ mảnh vườn.
E. Hoạt động tìm tòi mở rộngCâu 1 trang 138. Sgk
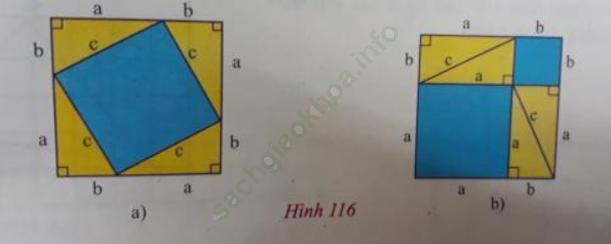
Câu 2 trang 139. Lấy bìa mỏng cắt thành 8 tam giác vuông bằng nhau. Trong mỗi tam giác vuông đó, ta gọi độ dài các cạnh góc vuông là a và b, gọi độ dài cạnh huyền là c. Cắt hai tấm bìa hình vuông bằng nhau có cạnh bằng a + b.
a) Đặt 4 tam giác vuông lên tấm bìa hình vuông như hình 116 a). Phần bìa không bị che lấp là một hình vuông có cạnh bằng c, tính diện tích phần bìa đó theo c.
b) Đặt bốn tam giác vuông còn lại lên tấm bìa hình vuông thứ hai như hình 116 b). Phần bìa không bị che lấp gồm hai hình vuông có cạnh là a và b, tính diện tích phần bìa đó theo a và b.
c) Từ đó rút ra nhận xét gì về quan hệ giữa c2 và a2 + b2
Trả lời:
a) Phần bìa còn lại là hình vuông có cạnh bằng c. Diện tích phần bìa còn lại là: S = c2.
b) Phần bìa còn lại là hai hình vuông có cạnh là a và b.
Diện tích hình vuông có cạnh là a là: S1 = a2
Diện tích hình vuông có cạnh là b là: S2 = b2
Diện tích phần bìa còn lại là: S′ = S1+S2 = a2 + b2.
c) Do hai hình vuông ban đầu đều có độ dài cạnh là a + b, và các tam giác là bằng nhau (theo cách cắt) ⇒ c2 = a2 + b2 Bài trước: Toán 7 VNEN Bài 5: Tam giác cân - Tam giác đều - trang 130 Bài tiếp: Toán 7 VNEN Bài 7: Luyện tập - trang 139