Toán 7 VNEN Bài 3: Trường hợp bằng nhau cạnh-góc-cạnh - trang 120
Thực hiện các hoạt động sau:
- Vẽ △ABC và △A′B′C′, biết AB = A’B’ = 2 cm; AC = A’C’ = 3 cm;
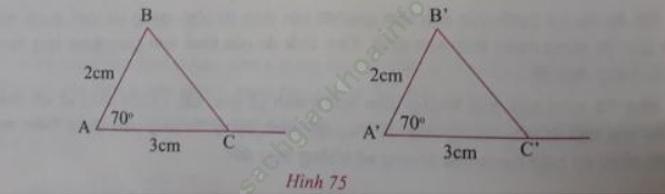
- Đo các cạnh BC và B’C’ rồi so sánh hai cạnh đó.
△ABC và △A′B′C′ có bằng nhau không? Vì sao?
Trả lời:
- Học sinh thực hiện vẽ tam giác bằng thước và compa vào vở.
- Dùng thước thẳng đo độ dài 2 cạnh BC và B’C’, ta thấy: BC = B’C’.
- Xét △ABC và △A′B′C′ có:
AB = A’B’ (giả thiết);
AC = A’C’ (giả thiết);
BC = B’C’;
Suy ra: △ABC = △A′B′C′.
B. Hoạt động hình thành kiến thứcCâu 1 trang 121 toán 7 VNEN tập 1.
a) Đọc kĩ nội dung sau (sgk trang 121)
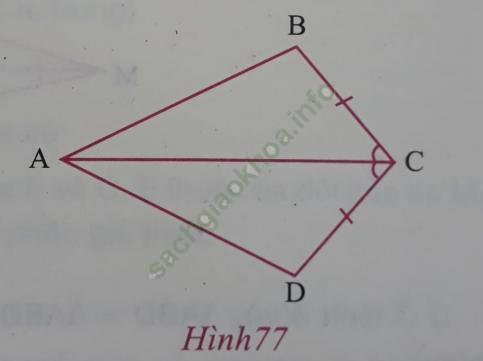
b) Cho hình 77. Em hãy viết kí hiệu thể hiện sự bằng nhau của hai tam giác trong hình đó. (Sgk trang 121)
Câu 2 trang 121.
a) Cho hình 78. Điền cụm từ thích hợp vào chỗ trống (…)
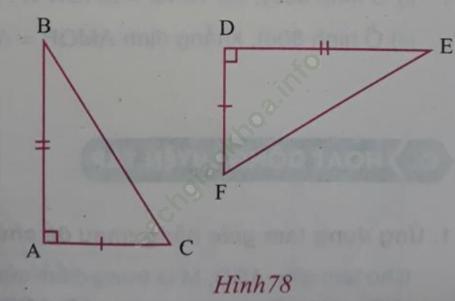
Xét △ABC và △DEF. Từ hình vẽ ta có:
AB = … (theo giả thiết);
AC = … (theo giả thiết).
Do đó △ABC=… (………).
b) Đọc kĩ nội dung sau (Sgk trang 121)
c) Em hãy quan sát các hình vẽ trên hình 80 và làm theo mẫu
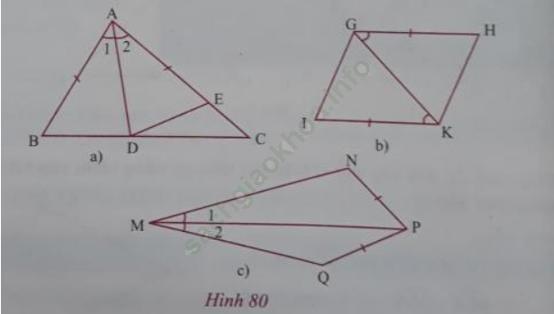
i) Ở hình 80a) △ABD=△AED vì đồng thời có: AB = AE; 
AD là cạnh chung.
ii) Ở hình 80b), có △IKG =△HGK vì: ……………………………; ……………………………. ; …………………………….
iii) Ở hình 80c), khẳng định △MPQ=△MPN đúng hay sai? Vì sao?
Trả lời:
a) Xét △ABC và △DEF. Từ hình vẽ ta có:
AB = DE (theo giả thiết);
AC = DF (theo giả thiết).
Do đó △ABC = △DEF (c. g. c)
c)
ii) Ở hình 80b), có △IKG = △HGK vì: GH = IK; 
ii) Ở hình 80c), khẳng định △MPQ = △MPN là sai vì hai tam giác này không có hai cạnh và một góc xen giữa bằng nhau.
C. Hoạt động luyện tậpCâu 1 trang 122. Ứng dụng tam giác bằng nhau để chứng minh hai đường thẳng song song
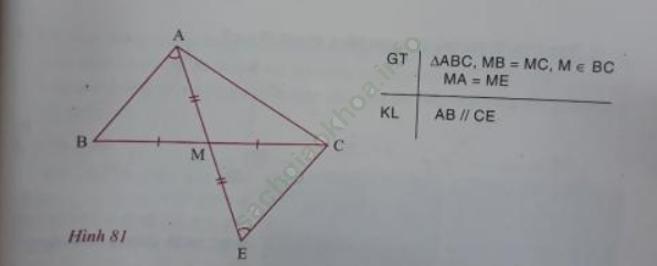
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh rằng AB // CE.
Dưới đây là hình vẽ và giả thiết kết luận của bài toán
Hãy sắp xếp lại năm câu sau đây một cách hợp lí để có lời giải bài toán trên:
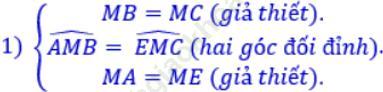
2) Do đó: △AMB=△MEC (c. g. c)
3) ⇒ AB // CE (có hai góc bằng nhau ở vị trí so le trong).
5) Xét hai tam giác AMB và EMC. Từ hình vẽ ta có:
Lưu ý: Để cho gọn, các quan hệ như M nằm giữa B và C, E thuộc tia đối của tia MA đã được thể hiện ở hình 81 nên có thể không ghi ở phần giả thiết.
Trả lời:
Thứ tự được sắp xếp đúng như sau: 5 → 1 → 2 → 4 → 3.
Câu 2 trang 123.
a) Vẽ tam giác ABC, biết 
, AB = AC = 3 cm. Sau đó đo góc B và góc C.
b) Nêu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây (h. 82) bằng nhau theo trường hợp cạnh – góc – cạnh:
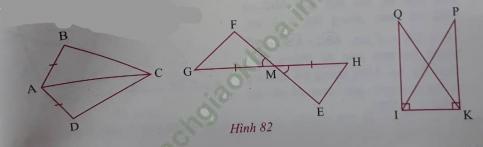
*) △ABC = △ADC;
**) △FMG = △EMH;
***) △QIK = △PKI.
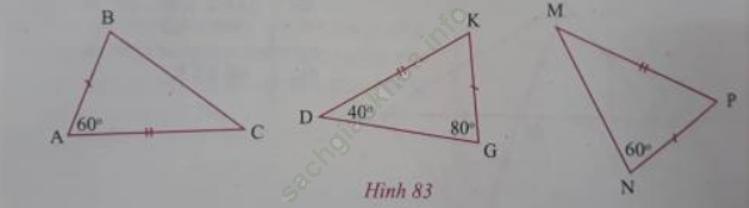
c) Trên hình 83 hai tam giác nào bằng nhau? Vì sao?
Trả lời:
a) Học sinh thực hiện các bước vẽ tam giác sử dụng thước thẳng và compa để được hình vẽ như dưới đây:
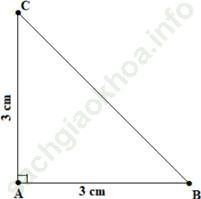
Dùng thước đo góc để đo góc B và góc C, ta được:
b)
*) Xét △ABC và △ADC có:
+ AC chung;
+ AB = AD.
⇒ Điều kiện để △ABC=△ADC theo trường hợp cạnh – góc – cạnh là:
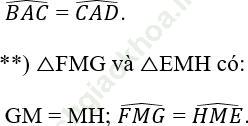
⇒ Điều kiện để △FMG=△EMH theo trường hợp cạnh – góc – cạnh là: FM = ME.
***) △QIK và △PKI có: IK chung;
⇒ Điều kiện để △QIK=△PKI theo trường hợp cạnh – góc – cạnh là: QI = PK.
c) Xét tam giác KGD có:
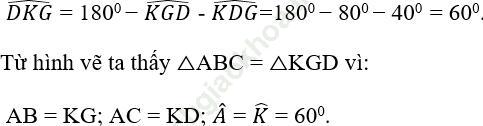
Câu 3 trang 124. Cho △ABC, có AB = AC. Kẻ tia phân giác góc A cắt BC tại M. Chứng minh rằng:
a) M là trung điểm của cạnh BC;
b) AM ⊥ BC.
Trả lời:
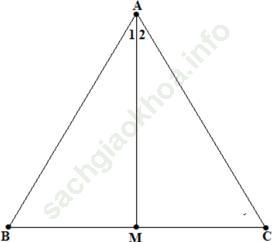
a) Xét △ABM và △ACM
AB = AC (theo giả thiết);
AM chung;
Do đó △ABM=△ACM (c. g. c)
⇒ MB = MC (hai cạnh tương ứng)
Xét đoạn thẳng BC có MB = MC (cmt) và M nằm giữa B và C, suy ra M là trung điểm của BC.
b) Theo câu a) △ABM=△ACM
Câu 1 trang 124. Cho góc xOy. Lấy điểm A trên tia Ox, điểm B trên tia Oy sao cho OA = OB. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD. Chứng minh rằng △OAD = △OBC.
Trả lời:
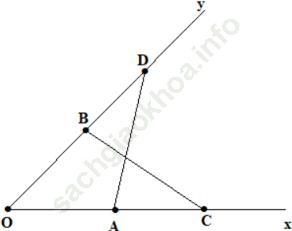
Xét △OAD và △OBC
OA = OB (theo giả thiết);
OD = OC (tổng của các đoạn thẳng bằng nhau);
Do đó △OAD=△OBC (c. g. c).
Câu 2 trang 124. Cho đoạn thẳng AB, từ điểm H là trung điểm của AB kẻ đường thẳng d vuông góc với AB, lấy M trên D. So sánh độ dài các đoạn thẳng MA và MB.
Trả lời:
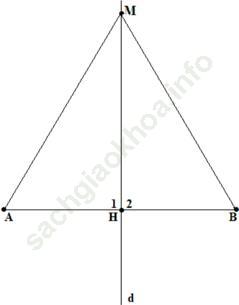
Xét △MAH và △MBH
AH = HB (theo giả thiết);
MH chung;
Do đó △MAH=△MBH (c. g. c).
⇒ MA = MB.
Câu 3 trang 124. Tìm các tia phân giác trên hình 84. Nói rõ chúng là tia phân giác của góc nào. Hãy chứng minh điều đó.
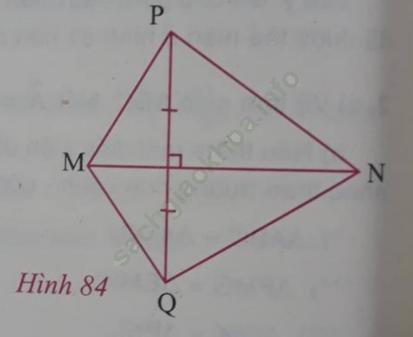
Trả lời:
Gọi H là giao điểm của hai đường thẳng MN và PQ.
Xét △PMH và △QMH
PH = HQ (theo giả thiết);
Suy ra MH là tia phân giác của góc PMQ.
Chứng minh tương tự: △PNH = △QMH (c. g. c)
hay NH là tia phân giác của góc PNQ.
Câu 4 trang 124.
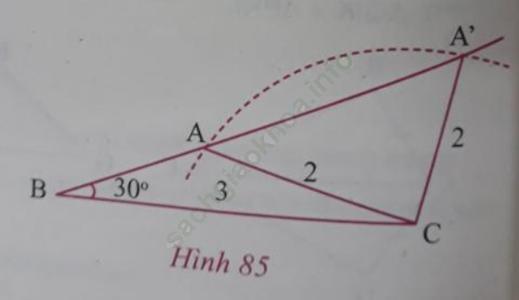
Trên hình 85, các tam giác ABC và A’BC có cạnh chung BC = 3 cm; CA = CA’ = 2 cm, 
nhưng hai tam giác đó không bằng nhau. Tại sao ở đây không thể áp dụng trường hợp cạnh – góc – cạnh để kết luận △ABC = △A′BC?
Trả lời:
Theo trường hợp bằng nhau cạnh – góc – cạnh của hai tam giác thì chúng cần có hai cạnh và một góc xen giữa tương ứng bằng nhau.
Hai tam giác ABC và A’BC có 2 cạnh và một góc bằng nhau nhưng góc đó không phải là góc xen giữa hai cạnh đó nên chúng không bằng nhau.
Câu 5 trang 125.
Đố: Một miếng bìa có dạng một hình chữ nhật. Chỉ bằng một nếp gấp thẳng em hãy chia hình chữ nhật đó thành hai tam giác vuông bằng nhau. Nếu được dùng hai nếp gấp thằng em có thể chia hình chữ nhật đó thành mấy cặp tam giác vuông bằng nhau?
Trả lời:
+) Nếu dùng một nếp gấp thẳng, em sẽ gấp theo một trong hai đường chéo của hình chữ nhật để được hai tam giác vuông bằng nhau.
+) Nếu được dùng hai nếp gấp thẳng, em có thể gấp theo hai đường chéo của hình chữ nhật để được 2 cặp tam giác bằng nhau. Bài trước: Toán 7 VNEN Bài 2: Trường hợp bằng nhau cạnh-cạnh-cạnh - trang 115 Bài tiếp: Toán 7 VNEN Bài 4: Trường hợp bằng nhau góc-cạnh-góc - trang 125