Bài 4: Đường trung tuyến của tam giác, tính chất ba đường trung tuyến của tam giác - trang 76 toán 7 VNEN tập 2
a) Đọc kĩ nội dung sau (Sgk trang 74)
b) Đọc và làm theo yêu cầu
- Cho tam giác ABC với các trung tuyến AD, BE, CF. Gọi G là trọng tâm của tam giác.
Vẽ hình theo giả thiết trên vào hình 39 rồi điền vào chỗ trống cho hợp lý.
- Cho G là trọng tâm tam giác DEF, DH là đường trung tuyến.
Trong các khẳng định sau, khẳng định nào đúng?
A. ![]()
C. ![]()
Bài giải:
Điền vào chỗ trống như sau:
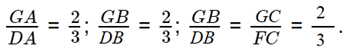
- Đáp án đúng là C
C. Hoạt động luyện tậpCâu 1. trang 76 toán 7 VNEN tập 2.
Đọc và làm theo yêu cầu:
a) Thực hành đo đạc (Sgk)
b) Cho hình 40. Điền số thích hợp vào chỗ trống (... ) trong mỗi đẳng thức sau (theo mẫu):
MG = 2 GR; GR =..... MR; GR =..... MG
NS =..... NG; NS =..... GS; NG =..... GS
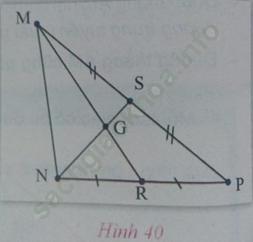
Bài giải:
b) MG = 2 GR; GR = ![]() MR; GR =
MR; GR = ![]() MG
MG
NS = ![]() NG; NS = 3 GS; NG = 2 GS
NG; NS = 3 GS; NG = 2 GS
Câu 2. trang 76. Hãy làm các bài tập sau:
Bài 1: Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho BE = ![]() BC. Gọi K là giao điểm của AE và CD. Chứng minh rằng DK = KC.
BC. Gọi K là giao điểm của AE và CD. Chứng minh rằng DK = KC.
Bài 2: Cho tam giác ABC cân tại A có AB = AC = 5cm, BC = 3cm. Kẻ trung tuyến AM.
a) Chứng minh rằng AM vuông góc với BC
b) Tính độ dài AM.
Bài giải:
Bài 1.
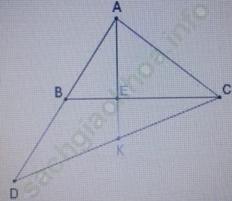
Ta có:
BE = ![]() BC
BC
Mà: BE + EC = BC
![]() BC + EC = BC
BC + EC = BC
⇒ EC = BC - ![]() BC =
BC = ![]() BC
BC
Xét ΔACD ta có:
CB là trung tuyến (vì AB = BD)
CE = ![]() BC; E ∈ BC
BC; E ∈ BC
⇒ E là trọng tâm của tam giác ACD.
Mà: E ∈ AK
⇒ AK là trung tuyến của tam giác ACD
⇒ K là trung điểm của DC nên DK = KC.
Bài 2:
a) Xét tam giác ABM và ACM có:
- AB = AC (gt)
- AM chung
- BM = CM (M la trung điểm của BC)
⇒ Tam giác ABM bằng tam giác ACM
⇒ ![]()
Mà ![]() = 180 độ (kề bù)
= 180 độ (kề bù)
⇒ ![]() = 90 độ ⇒ AM vuông góc với BC.
= 90 độ ⇒ AM vuông góc với BC.
b) Ta có: BM = CM = BC: 2 = 1.5
Theo câu a có tam giác ABM vương tại M. Áp dụng định lý Pitago ta có:
AB2 = AM2 + BM2
⇒ AM2 = AB2 - BM2
⇒ AM2 = 52 - (1.5)2
⇒ AM = ![]()
Câu 1. trang 77 toán 7 VNEN tập 2.
Cho tam giác ABC, có G là trọng tâm. Diện tích của các tam giác AGB, BGC và AGC có bằng nhau hay không (h. 41)?
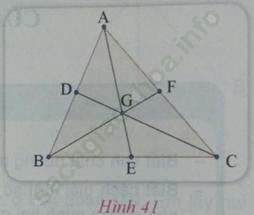
Bài giải:
- Ta có: AE là trung tuyến của tam giác ABC nên SΔ ABE = SΔ ACE = ![]() SΔ ABC
SΔ ABC
Do G là trọng tâm của tam giác ABC nên ta có: AG = ![]() AE; GE =
AE; GE = ![]() AE
AE
Xét Δ ABE, Δ ABG và Δ BGE có:
+) chung đường cao hạ từ B
+) AG = ![]() AE; GE =
AE; GE = ![]() AE
AE
Suy ra:
+) SΔ ABG = 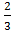 SΔ ABE =
SΔ ABE = 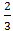 .
. 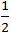 . SΔ ABC =
. SΔ ABC = 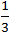 SΔ ABC
SΔ ABC
+) SΔ BGE = 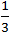 SΔ ABE =
SΔ ABE = 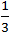 .
. 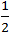 . SΔ ABC =
. SΔ ABC = ![]() SΔ ABC
SΔ ABC
- Tương tự ta có:
+) SΔ ACG = 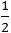 SΔ ABC
SΔ ABC
+) SΔ CGE = ![]() SΔ ABC
SΔ ABC
Suy ra: SΔ BGC = SΔ BGE + SΔ CGE = 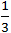 SΔ ABC
SΔ ABC
Nên: SΔ ABG = SΔ ACG = SΔ BGC
E. Hoạt động tìm tòi mở rộngCâu 1. trang 77 toán 7 VNEN tập 2.
Một chiếc bánh ga-tô đặc biệt có hình tam giác. Làm thế nào để chia chiếc bánh này thành ba phần bằng nhau đều có dạng hình tam giác, mà mỗi phần đều chứa một cạnh của tam giác ban đầu?
Bài giải:
- Để chia chiếc bánh này thành ba phần bằng nhau đều có dạng hình tam giác, mà mỗi phần đều chứa một cạnh của tam giác ban đầu, ta làm như sau:
+ B1: Xác định trọng tâm của tam giác
+ B2: Nối trọng tâm với các đỉnh của tam giác
+ B3: Cắt bánh theo các đường nối ở bước 2
Bài trước: Bài 3: Quan hệ giữa đường vuông góc và đường xiên, quan hệ giữa đường xiên và hình chiếu của nó - trang 69 toán 7 VNEN tập 2 Bài tiếp: Bài 5: Tính chất đường trung trực của một đoạn thẳng - trang 78 toán 7 VNEN tập 2