Toán 7 VNEN Bài 5: Hàm số - trang 64
Đọc các ví dụ rồi điền vào chỗ trống (... ) cho thích hợp
Ví dụ 1: Độ tuổi và chiều cao của loài hươu cao cổ có mối liên hệ như trong bảng dưới đây:
| Độ tuổi (năm) | Chiều cao (m) |
| 14 | 4,25 |
| 18 | 4,40 |
| 20 | 4,85 |
| 21 | 5,00 |
Nhận xét: Chiều cao của loài hươu cao cổ phụ thuộc vào...
Ví dụ 2: Bảng dưới đây cho biết nhiệt độ (T
| t (giờ) | 0 | 4 | 8 | 12 | 16 | 20 |
| (T | 20 | 18 | 22 | 26 | 24 | 21 |
Nhận xét:
a) Nhiệt độ (T
b) Với mỗi giá trị của t ta luôn xác định được chỉ một giá trị tương ứng của...
Ta nói: T là hàm số của t.
Trả lời:
Ví dụ 1: Chiều cao của loài hươu cao cổ phụ thuộc vào độ tuổi của nó.
Ví dụ 2:
a) Nhiệt độ (T
b) Với mỗi giá trị của t ta luôn xác định được chỉ một giá trị tương ứng của nhiệt độ T. Ta nói: T là hàm số của t.
B. Hoạt động hình thành kiến thứcCâu 1 trang 65 toán 7 VNEN tập 1. Trả lời câu hỏi rồi điền vào chỗ trống (... ) cho thích hợp
a) Khối lượng m (g) của một thanh kim loại đồng chất có khối lượng riêng là 7,8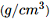 
) tỉ lệ thuận với thể tích V 
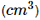theo công thức: m = 7,8V.
- Tính các giá trị tương ứng của m khi biết V nhận các giá trị là: 1; 2; 3; 4.
- Với mỗi giá trị của V ta luôn xác định được chỉ một giá trị tương ứng của...
b) Thời gian t (giờ) của một vật chuyển động đều tỉ lệ nghịch với vận tốc v (km/giờ) của nó theo công thức: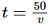 
- Tính giá trị tương ứng của t khi biết v = 5; 10; 15; 20.
- Với mỗi giá trị của v ta luôn xác định được chỉ một giá trị tương ứng của...
Trả lời:
a)
Thay lần lượt các giá trị của V vào công thức m = 7,8V để tính các giá trị tương ứng của m.
+ Khi V = 1 thì m = 7,8 x 1 = 7,8;
+ Khi V = 2 thì m = 7,8 x 2 = 15,6;
Làm tương tự như vậy ta có bảng sau:
| V | 1 | 2 | 3 | 4 |
| m | 7,8 | 15,6 | 23,4 | 31,2 |
- Với mỗi giá trị của V ta luôn xác định được chỉ một giá trị tương ứng của m.
b) Ta có bảng sau:
- Với mỗi giá trị của v ta luôn xác định được chỉ một giá trị tương ứng của t.
Câu 2 trang 66.
a) Đọc kĩ nội dung sau (Sgk trang 66)
b) Chú ý (Sgk trang 66)
c) Cho hàm số y = 5x – 1. Tính các giá trị tương ứng của y khi:
d)
Trả lời:
c) Thay các giá trị của x vào biểu thức của hàm số để tính các giá trị y tương ứng.
+ Khi x = -5, thì y = 5x (-5) – 1 = - 26;
Tương tự với các giá trị khác của x, ta được bảng các giá trị y, x tương ứng sau:
d)
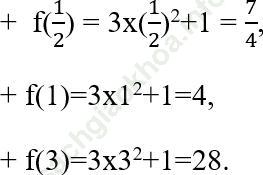
Câu 1 trang 67. Các giá trị tương ứng của hai đại lượng x và y được cho trong bảng sau. Đại lượng y có phải là hàm số của đại lượng x không?
a)
| x | -4 | -3 | -2 | -1 | 2 | 2 | 3 | 4 |
| y | 16 | 9 | 4 | 1 | 1 | 4 | 9 | 16 |
b)
c)
| x | -0 | 1 | 2 | 3 | 4 |
| y | 2 | 2 | 2 | 2 | 2 |
Trả lời:
Theo khái niệm hàm số, y là hàm số của x khi với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y.
a) Đại lượng y không phải là hàm số của x vì với cùng một giá trị x = 2 ta nhận được 2 giá trị của y là y = 1 và y = 4.
b) Đại lượng y là hàm số của đại lượng x vì với mỗi giá trị của x ta nhận được chỉ một giá trị của y.
c) Đại lượng y là hàm số của đại lượng x vì với mỗi giá trị của x ta xác định được tương ứng một giá trị của y. Trong bảng này thì y là hàm hằng.
Câu 2 trang 67. Cho hàm số y=f (x)=8x2−1. Tính f (2); f (-2); f (0).
Trả lời:
+ f (2) = 8×22–1 = 31;
+ f (−2) = 8× (−2)2–1 = 31;
+ f (0) = 8×02–1 = −1.
Câu 3 trang 67. Cho hàm số y=5x−1. Lập bảng các giá trị tương ứng của y khi: x = -5; -4; -3; -2.
Trả lời:
Thay lần lượt các giá trị của x vào y = 5x−1 để tìm các giá trị tương ứng của y rồi lập thành bảng như sau:
| x | -5 | -4 | -3 | -2 |
| y | -26 | -21 | -16 | -11 |
Câu 4 trang 67. Cho hàm số y = f (x) = 
.
a) Tính f (5); f (-3).
b) Hãy điền các giá trị tương ứng của hàm số sau vào bảng:
Trả lời:
a) Thay các giá trị của x vào biểu thức của hàm số, ta được:
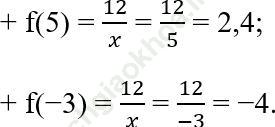
b)
Câu 5 trang 67. Cho hàm số y = f (x) = x2−2. Tính f (2); f (1); f (0); f (-1); f (7).
Trả lời:
+ f (2) = x2–2 = 22–2 = 2;
+ f (1) = x2–2 = 12–2 = −1;
+ f (0) = x2–2 = 02–2 = −2;
+ f (−1) = x2–2 = (−1)2–2 = −1;
+ f (7) = x2–2 = 72–2 = 45.
Câu 6 trang 67. Cho hàm số y = f (x) = 1–8x. Khẳng định nào sau đây là đúng?
Trả lời:
Ta tính các giá trị tương ứng của hàm số:
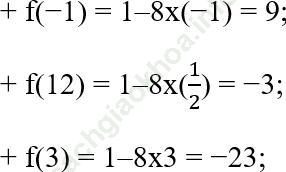
Vậy:
a) Đúng;
b) Sai;
c) Sai.
D. E. Hoạt động vận dụng & Tìm tòi mở rộngCâu 1 trang 68.
Bài toán: Ánh sáng đi với vận tốc 300000 km/s. Hàm số d = 300000t mô tả quan hệ giữa khoảng cách d và thời gian t.
a) Ánh sáng đi được quãng đường dài bao nhiêu kilomet trong 20 giây?
b) Ánh sáng đi được quãng đường dài bao nhiêu kilomet trong 1 phút?
Lời giải:
a) Trong 20 giây quãng đường đi được của ánh sáng là: d = 300000x20 = 6000000 (km).
b) Trong 1 phút quãng đường đi được của ánh sáng là:
Đổi: 1 phút = 60 giây;
d = 300000x60 = 18000000 (km) Bài trước: Toán 7 VNEN Bài 4: Một số bài toán về đại lượng tỉ lệ nghịch - trang 61 Bài tiếp: Toán 7 VNEN Bài 6: Mặt phẳng tọa độ - trang 69