Bài 7: Tính chất tia phân giác của một góc, đường phân giác của tam giác - trang 85 toán 7 VNEN tập 2

A. B. Hoạt động khởi động và hình thành kiến thức

Câu 1. trang 85 toán 7 VNEN tập 2. Thực hiện các thao tác sau (Sgk)

Câu 2. trang 86.

a) b) (Sgk)

c) Đọc và làm theo yêu cầu

Cho tứ giác ABDC (h. 63) có AB = AD, AB vuông góc với BC, AD vuông góc với CD. Chứng minh AC là phân giác của góc BAD.

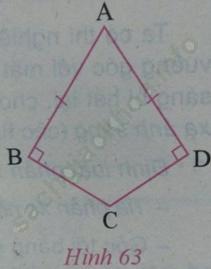
Trả lời:

Xét 2 tam giác ABC và ADC, có:

- AB = AD (gt)

- AC chung

- (=90 độ)

⇒ Δ ABC = Δ ADC (c. g. c)

⇒ hay AC là phân giác của góc BAD

C. Hoạt động luyện tập

Câu 1. trang 87 toán 7 VNEN tập 2. Thực hành (Sgk)

Câu 2. trang 87. Luyện tập, ghi vào vở

Bài 1. Cho khác góc bẹt. Trên tia Ox lấy hai điểm A và B. trên tia Oy lấy hai điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng:

a) Δ BOC = Δ DOA

b) BC = AD

c) IA =IC, IB = ID

d) OI là tia phân giác của góc xOy.

Bài 2. Có một mảnh sắt phẳng hình dạng một góc (h. 65) và một thước thẳng có chia khoảng. Làm thế nào để vẽ được tia phân giác của góc này?

Bài giải:

Bài 1.

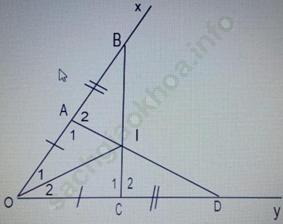
a) Xét hai tam giác BOC và DOA, có:

- OA = OC (gt)

- OB = OD (gt)

- O là góc chung

⇒ Δ BOC = Δ DOA (c. g. c)

b) Xét hai tam giác AIB và CID có:

- (vì Δ BOC = Δ DOA) (1)

Ta có:

- OB = OA + AB

- OD =OC + CD

mà OB = OD

- OA = OC

⇒ AB = CD (2)

c) Ta lại có:

- = 180 độ

- = 180 độ

Mặt khác:

- (vì Δ BOC = Δ DOA)

⇒ (3)

Từ (1), (2) và (3) ⇒ Δ AIB = Δ CID (g. c. g) ⇒ IA = IC và IB = ID (2 cặp cạnh tương ứng)

d) Xét Δ OAI và Δ OCI có:

- OI là cạnh chung

- IA = IC (cmt)

- (vì Δ BOC = Δ DOA)

⇒ Δ OBI = Δ ODI (c. g. c)

⇒ (2 góc tương ứng)

⇒ OI là tia phân giác của góc xOy (đpcm)

Bài 2.

- Gọi đỉnh góc đó là O. Ở trên 2 viền là 2 cạnh tương ứng để tạo thành góc đã cho của mảnh sắt.

Lần lượt lấy 2 cặp điểm A, B và C, D sao cho OA = OC và OB = OD

Nối A với D và B với C thì cắt nhau tại điểm gọi là I

Nối O và I ta được OI là tia phân giác của mảnh sắt.

D. E. Hoạt động vận dụng và tìm tòi mở rộng

Câu 2. trang 88 toán 7 VNEN tập 2.

Chứng minh định lý: Nếu một tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân.

Bài giải:

Xét tam giác ABC:

AH là đường trung tuyến đồng thời là đường trung trực nên AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:

HB = HC

AH là cạnh chung

Nên Δ HAB = Δ HAC ⇒ AB = AC

Vậy Δ ABC cân tại A

Bài trước: Bài 6: Tính chất ba đường trung trực của tam giác - trang 81 toán 7 VNEN tập 2 Bài tiếp: Bài 8: Tính chất ba đường phân giác của tam giác - trang 89 toán 7 VNEN tập 2