Toán 7 VNEN Bài 10: Ôn tập chương 2 - trang 148
Câu 1 trang 148 toán 7 VNEN tập 1. Thực hiện các hoạt động sau:
Một bạn hỏi, một bạn trả lời, sau đó đổi vai cho nhau.
a) Nhớ lại và trao đổi
Hãy nhớ lại và nói với bạn về các kiến thức mà em đã học ở chương này
(1) Hai tam giác bằng nhau là hai tam giác như thế nào?
(2) Có mấy trường hợp bằng nhau của hai tam giác? Nêu các trường hợp đó.
(3) Nêu các trường hợp bằng nhau của tam giác vuông.
(4) Phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh một tam giác là một tam giác cân.
(5) Phát biểu định nghĩa và tính chất tam giác đều. Nêu các cách chứng minh một tam giác là một tam giác đều.
(6) Phát biểu định lý Py-ta-go thuận và đảo.
b) Trả lời các câu hỏi sau
(1) Thế nào là hai tam giác bằng nhau?
(2) Thế nào là tam giác cân?
(3) Thế nào là tam giác vuông cân?
(4) Thế nào là tam giác đều?
(5) Nêu các tính chất của tam giác cân.
(6) Nêu các tính chất của tam giác vuông cân.
(7) Nêu các tính chất của tam giác đều.
c) Đố bạn nêu chính xác các tính chất sau:
(1) Nếu ba cạnh của tam giác này … tam giác kia, thì hai tam giác đó bằng nhau.
(2) Nếu hai cạnh và góc xen giữa của tam giác này … tam giác kia, thì hai tam giác đó bằng nhau.
(3) Nếu một cạnh và hai góc kề của tam giác này … tam giác kia, thì hai tam giác đó bằng nhau.
(4) Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này … tam giác vuông kia, thì hai tam giác đó bằng nhau.
(5) Nếu cạnh huyền và một góc nhọn của tam giác vuông này … tam giác kia, thì hai tam giác đó bằng nhau.
(6) Nếu hai cạnh của tam giác vuông này … tam giác vuông kia, thì hai tam giác đó bằng nhau.
(7) Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này … tam giác vuông kia, thì hai tam giác đó bằng nhau.
(8) Trong một tam giác vuông, bình phương cạnh huyền bằng … cạnh góc vuông.
(9) Nếu một tam giác có bình phương của một cạnh bằng … đó là tam giác vuông.
Trả lời:
a)
(1) Hai tam giác bằng nhau là hai tam giác có ba cạnh bằng nhau và ba góc bằng nhau.
(2) Có 3 trường hợp bằng nhau của hai tam giác, đó là:
+ cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia, thì hai tam giác đó bằng nhau;
+ cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia, thì hai tam giác đó bằng nhau.
+ góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia, thì hai tam giác đó bằng nhau.
(3) Các trường hợp bằng nhau của tam giác vuông:
+ Cạnh góc vuông – góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia, thì hai tam giác đó bằng nhau.
+ Cạnh huyền – góc nhọn: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác kia, thì hai tam giác đó bằng nhau.
+ Hai cạnh góc vuông: Nếu hai cạnh của tam giác vuông này hai cạnh góc vuông của tam giác vuông kia, thì hai tam giác đó bằng nhau.
+ Cạnh huyền – cạnh góc vuông: Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia, thì hai tam giác đó bằng nhau.
(4) Định nghĩa tam giác cân: Tam giác cân là tam giác có hai cạnh bằng nhau.
Tính chất:
+ Trong một tam giác cân, hai góc ở đáy bằng nhau;
+ Trong một tam giác cân, hai cạnh bên bằng nhau;
+ Nếu một tam giác có hai góc bằng nhau thì đó là tam giác cân.
Các cách chứng minh một tam giác là tam giác cân:
+ Chứng minh một tam giác có hai cạnh bằng nhau.
+ Chứng minh một tam giác có hai góc bằng nhau.
(5) Định nghĩa tam giác đều: Tam giác đều là tam giác có ba cạnh bằng nhau.
Tính chất:
+ Trong một tam giác đều, mỗi góc có số đo bằng 600.
+ Nếu một tam giác có ba góc bằng nhau thì đó là tam giác đều;
+ Nếu một tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều.
Các cách chứng minh một tam giác là tam giác đều:
+ Chứng minh một tam giác có ba cạnh bằng nhau;
+ Chứng minh một tam giác có ba góc bằng nhau;
+ Chứng minh một tam giác cân có một góc bằng 600.
(6)
+) Định lý Py-ta-go thuận: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
+ Định lý Py-ta-go đảo: Nếu một tam giác có bình phương của một cạnh bằng tổng bình phương hai cạnh còn lại thì đó là tam giác vuông.
b) c) Các em xem lại kiến thức đã được nêu trong phần a để trả lời câu hỏi và điền vào chỗ trống.
Câu 2 trang 150. Đọc kĩ nội dung sau (Sgk)
Câu 3 trang 151. Luyện tập
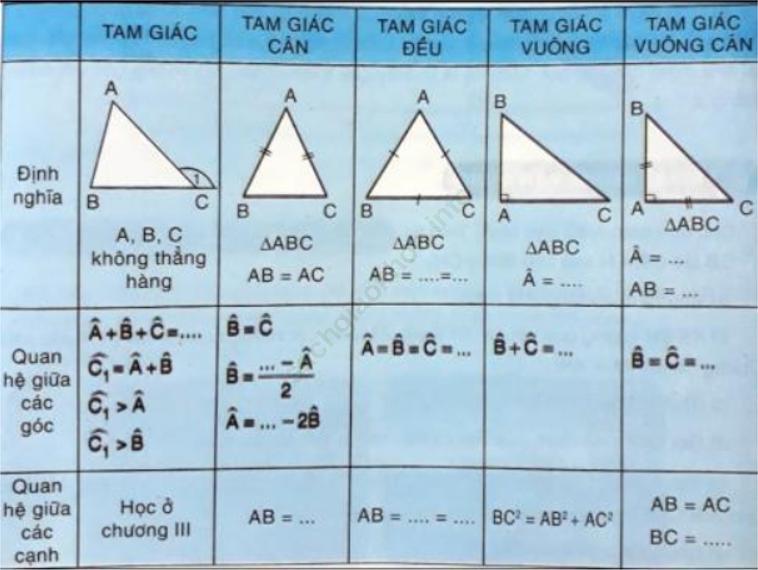
a) Điền cụm từ tích hợp vào chỗ trống (…) trong bảng sau:
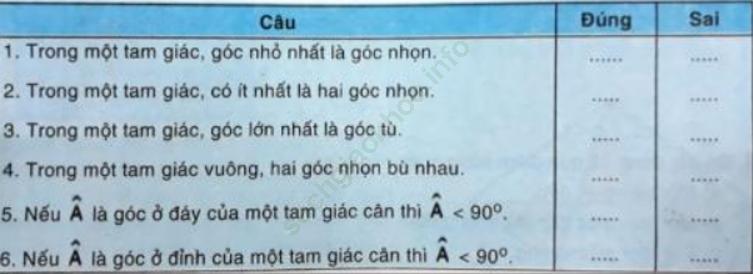
b) Điền dấu “x” vào chỗ trống một cách thích hợp:
c) Các tính chất sau đây được suy ra trực tiếp từ định lý nào?
i) Góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.
ii) Trong một tam giác vuông, hai góc nhọn phụ nhau.
iii) Trong một tam giác đều, các góc bằng 600.
iv) Nếu một tam giác có ba góc bằng nhau thì đó là tam giác đều.
d) Cho điểm A nằm ngoài đường thẳng a. Vẽ cung tròn tâm A cắt đường thẳng a ở B và C. Vẽ các cung tròn tâm B và C có cùng bán kính sao cho chúng cắt nhau tại một điểm khác A, gọi đó là điểm D. Hãy giải thích vì sao AD vuông góc với đường thẳng a.
Trả lời:
a)
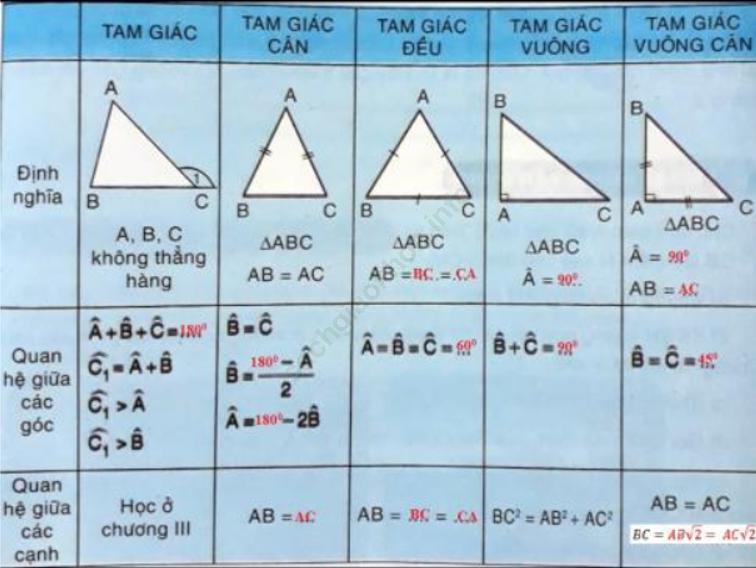
b)
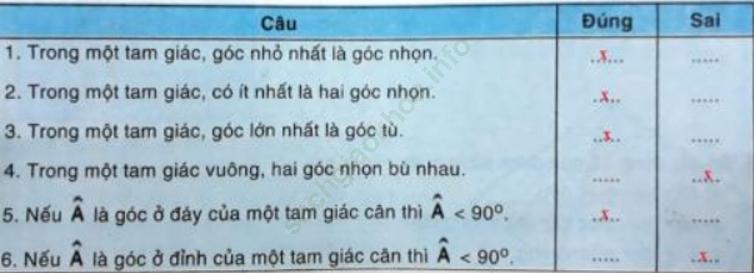
c) Các tính chất trên được suy ra trực tiếp từ định lý “Tổng ba góc trong tam giác. ”
d)

Câu 1 trang 152 toán 7 VNEN tập 1. Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN.
a) Chứng minh rằng AM = AN.
b) Kẻ BH vuông góc với AM (H thuộc AM), kẻ CK vuông góc với AN (K thuộc AN). Chứng minh HM = KN;
c) Chứng minh △BHA = △CKA;
d) Gọi O là giao điểm của BH và CK. Hỏi △OBC là tam giác gì? Vì sao?
e) Khi ![]() và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và cho biết OBC là tam giác gì.
và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và cho biết OBC là tam giác gì.
f) Chứng minh rằng AO ⊥ BC.
Trả lời:
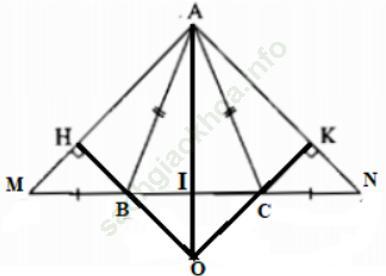
a) Xét △ABM và △ACN có:
AB = AC (giả thiết);
BM = CN (giả thiết);
⇒ △ABM = △ACN (c. g. c)
⇒ AM = AN (hai cạnh tương ứng).
b) Xét △HBM và △KCN vuông tại H và K có:
BM = CN (giả thiết);
⇒ △HBM = △KCN (cạnh huyền – góc nhọn);
⇒ HM = KN (hai cạnh tương ứng);
c) Xét △HBA và △KCA vuông tại H và K có:
AB = AC (giả thiết);
AH = AK (hiệu của những đoạn thẳng bằng nhau);
⇒ △HBA = △KCA (cạnh huyền – cạnh góc vuông);
d)

e)
Tính số đo các góc của △AMN:
Khi ![]() thì △ABC là tam giác đều.
thì △ABC là tam giác đều.
⇒ ![]() = 120∘ (các góc kề bù với các góc có số đo là 60∘.
= 120∘ (các góc kề bù với các góc có số đo là 60∘.
Khi BM = CN = BC thì △ABM và △ACN là các tam giác cân tại B và C có góc ở đỉnh là 120∘
Mặt khác: Theo câu a) △AMN cân tại M.

f) Gọi I là giao điểm của AO và BC.
Xét △AOH và △AOK vuông tại H và K có:
AO chung;
AH = AK (theo phần c: △HBA=△KCA);
⇒ △AOH = △AOK (cạnh huyền – cạnh góc vuông);
Xét △ABI và △ACI có:
AB = AC (giả thiết);

Hay AO ⊥ BC.
Câu 2 trang 152. Tam giác ABC trên giấy kẻ ô vuông có là tam giác vuông không? Vì sao?
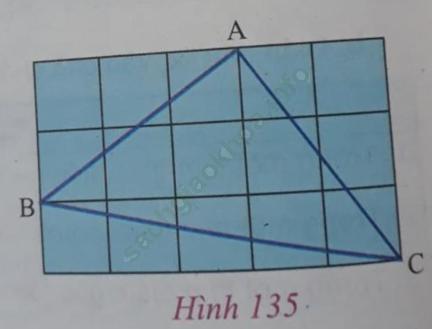
Trả lời:
Coi mỗi ô vuông là một đơn vị, từ hình vẽ ta có:
+ AB2 = 22 +32 = 13 (đơn vị);
+ BC2 = 12 + 52 = 26 (đơn vị);
+ AC2 = 22 + 32 = 13 (đơn vị);
△ABC có BC2 = AB2 + AC2 nên là tam giác vuông tại A.
Câu 3 trang 152. Đố em dùng 12 que diêm bằng nhau xếp thành:
a) Một tam giác đều;
b) Một tam giác cân mà không đều;
c) Một tam giác vuông;
Trả lời:
a) Các em xếp 12 que diêm thành một hình tam giác đều có cạnh bằng 4 que diêm.
b) Có rất nhiều tam giác cân mà không đều xếp được từ 12 que diêm.
Ví dụ: Các em xếp 12 que diêm thành một hình tam giác cân có hai cạnh bên là 3 que diêm, cạnh đáy dài 6 que diêm.
c) Các em xếp 12 que diêm thành một hình tam giác vuông có độ dài cạnh huyền là 5 que diêm, độ dài hai cạnh góc vuông lần lượt là 3 và 4 que diêm.
Câu 4 trang 152. Trên hình 136, một cầu trượt có đường lên BA dài 5 m, độ cao AH của nó là 3 m, còn các độ dài BC là 10 m và CD là 2 m. Bạn Mai nói rằng đường trượt tổng cộng AC + CD lớn hơn hai lần đường lên BA. Bạn Vân nói rằng điều đó không đúng. Theo em, ai đúng, ai sai?
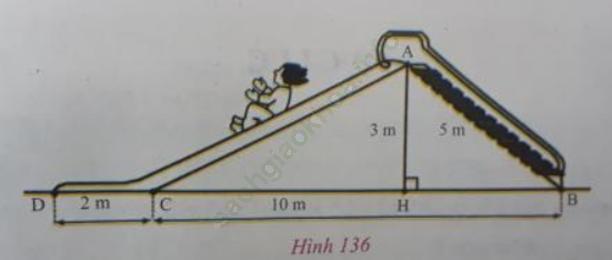
Trả lời:
Độ dài đoạn AC là:
Áp dụng định lý Py-ta-go cho △AHC vuông tại H:
Độ dài đường trượt là: AC + CD ≈ 10,44 + 2 ≈ 12,44 (m) > 2×BA = 2×5 = 10.
Bài trước: Toán 7 VNEN Bài 9: Thực hành ngoài trời về tam giác,tam giác bằng nhau - trang 146 Bài tiếp: Bài 1: Thu thập số liệu thống kê, tần số - trang 3 toán 7 VNEN tập 2