Ôn tập chương 3 - Phần Hình học - trang 52 sách bài tập Toán 7 Tập 2

Bài 82 trang 52 sách bài tập Toán 7 Tập 2: Cho tam giác ABC có AB < AC. Trên tia đối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.

a. Hãy so sánh các góc AMB và ANC.

b. Hãy so sánh các độ dài AM và AN.

Bài giải: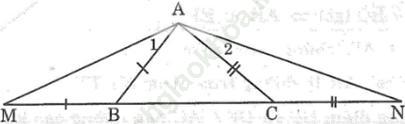

a. Trong Δ ABC, ta có AC > AB

Suy ra: ∠ (ABC) > ∠ (ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)

Ta có: AB = BM (gt) ⇒ Δ ABM cân tại B

Suy ra: ∠ (AMB) = ∠ A₁(tính chất tam giác cân)

Trong Δ ABM, ta có ∠ (ABC) là góc ngoài tại đỉnh B

Suy ra: ∠ (ABC) = ∠ (AMB) + ∠ A₁ hay: ∠ (ABC) = 2. ∠ (AMB)

Suy ra: ∠ (AMB) = 1/2 ∠ (ABC) (2)

Lại có: AC = CN (gt) ⇒ Δ ACN cân tại C

Suy ra: ∠ (ANC) = ∠ A₂(tính chất tam giác cân)

Trong Δ ACN, ta có ∠ (ACB) là góc ngoài tại đỉnh C

Suy ra: ∠ (ACB) = ∠ (ANC) + ∠ A₂ hay ∠ (ACB) = 2∠ (ANC)

Suy ra: ∠ (ANC) = 1/2 ∠ (ACB) (3)

Từ (1), (2) và (3) suy ra: ∠ (AMB) > ∠ (ANC).

b. Trong Δ AMN, ta có: ∠ (AMB) > ∠ (ANC)

Suy ra: AN > AM (đối diện với góc lớn hơn là cạnh lớn hơn).

Bài 83 trang 52: Cho tam giác ABC có AB < AC, đường cao AH. Chứng minh rằng: HB < HC, ∠ (HAB) < ∠ (HAC)(xét hai trường hợp: B nhọn và B tù).

Bài giải:

Ta có: AB < AC (giả thiết)

=> HB < HC (đường xiên lớn hơn thì hình chiếu lớn hơn)

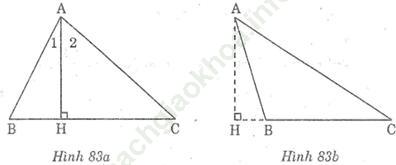
* Trường hợp góc B là góc nhọn (hình 83a)

Trong Δ ABC, ta có: AB < AC

=> ∠ B > ∠ C (đối diện với cạnh lớn hơn là góc lớn hơn)

Trong Δ AHB, ta có ∠ (AHB) = 90^o

=> ∠ B + ∠ (HAB) = 90^o (tính chất tam giác vuông) (1)

Trong Δ AHC, ta có ∠ (AHC) = 90^o

=> ∠ C + ∠ (HAC) = 90^o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: ∠ B + ∠ (HAB) = ∠ C + ∠ (HAC)

Mà ∠ B > ∠ C nên ∠ (HAB) < ∠ (HAC)

* Trường hợp Btù (hình 83b)

Vì điểm B nằm giữa H và C nên ∠ (HAC) = ∠ (HAB) + ∠ (BAC)

Vậy ∠ (HAB) < ∠ (HAC).

Bài 84 trang 52: Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm.

Bài giải:

Ta có: 1 = 3 - 2 = 4 - 3 = 5 - 4

=> Trong 3 cạnh của tam giác không có cạnh nào có độ dài 1cm.

* Nếu cạnh nhỏ nhất là 2cm

Ta có: 4 - 3 < 2 < 4 + 3; 5 - 4 < 2 < 5 + 4

=> hai cạnh kia là 3cm và 4cm hoặc 4cm và 5cm

* Nếu cạnh nhỏ nhất là 3cm

Ta có: 5 - 4 < 3 < 5 + 4; 3 = 5 - 2; 3 > 4 - 2

Như vậy hai cạnh kia là 5cm và 4cm

* Không có trường hợp cạnh nhỏ nhất là 4cm

Vậy có thể vẽ được ba tam giác với độ dài các cạnh là:

2cm; 3cm; 4cm

2cm; 4cm; 5cm

3cm; 4cm; 5cm

Bài 85 trang 53: Cho bốn điểm A, B, C, D như hình bên. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.

Bài giải: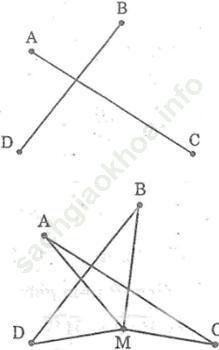

* Nếu M không trùng với giao điểm của AC và BD

Trong Δ AMC, ta có: MA + MC > AC (bất đẳng thức tam giác)

Trong Δ MBD, ta có: MB + MD > BD (bất đẳng thức tam giác)

* Nếu M trùng với giao điểm AC và BD

Ta có: MA + MC = AC

MB + MD = BD

+) Kết hợp cả hai trường hợp, suy ra: MA + MC ≥ AC

Và MB + MD ≥ BD (dấu bằng xảy ra khi M trùng với giao điểm của AC và BD)

Suy ra: MA + MB + MC + MD ≥ AC + BD

Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD.

Bài 86 trang 53: Cho hình sau trong đó G là trọng tâm của tam giác ABC. Chứng minh rằng:

a. S_AGC = 2S_GMC

b. S_GMB = S_GMC

c. S_AGB = S_AGC = S_BGC

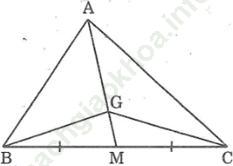
Bài giải:

a. Vì G là trọng tâm của Δ ABC nên GA = 2GM (tính chất đường trung tuyến)

Ta có Δ AGC và Δ GMC có chung đường cao kẻ từ đỉnh C đến AM, đồng thời cạnh đáy GA = 2GM.

=> S_AGC = 2S_GMC (1)

b. Ta có Δ GMB và Δ GMC có cạnh đáy MB = MC, chung đường cao kẻ từ đỉnh G đến cạnh BC

=> S_GMB = S_GMC (2)

c. Ta có Δ AGB và Δ GMB có chung đường cao kẻ từ đỉnh B đến cạnh AM, đồng thời AG = 2GM (chứng minh trên)

=> S_AGB = 2S_GMB (3)

Mà S_BGC = S_GMB + S_GMC = S_GMB + S_GMB = 2S_GMB (4)

Từ (1), (2), (3) và (4) suy ra: S_AGB = S_AGC = S_BGC

Bài 87 trang 53: Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy.

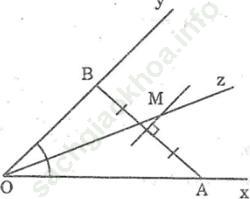
a. Hãy tìm điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠ (xOy); cách đều Ox, Oy và cách đều A, B.

b. Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a?

Bài giải:

a. Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠ (xOy).

Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.

Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠ (xOy)

Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.

b. Nếu OA = OB thì Δ OAB cân tại O

Khi đó tia phân giác của ∠ (xOy) cũng là đường trung trực của AB

Vậy bất kì điểm M nào nằm trên tia phân giác của ∠ (xOy) đều thỏa mãn điều kiện trong câu a).

Bài 88 trang 53: Cho góc xOy khác góc bẹt. Dùng một chiếc thước thẳng có chia khoảng, hãy nêu cách vẽ tia phân giác của góc xOy.

Bài giải: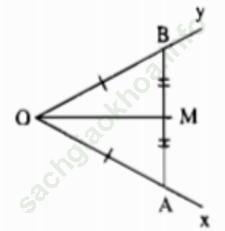

- Dùng thước chia khoảng, trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB.

- Nối AB.

- Dùng thước chia khoảng để đo đoạn AB, lấy trung điểm M của AB.

- Kẻ tia OM.

Khi đó, OM là tia phân giác của góc ∠xOy.

Chứng minh:

Tam giác ABO có OA = OB (cách dựng) nên tam giác OAB cân tại O.

Lại có: OM là đường trung tuyến nên OM cũng là đường phân giác của ∠ (AOB). (tính chất tam giác cân)

Vậy OM là tia phân giác của ∠ (xOy).

Bài 89 trang 53: Cho hình dưới trong đó giao điểm O của hai đường thẳng a và b nằm ngoài phạm vi tờ giấy. Chỉ vẽ hình trong phạm vi tờ giấu, hãy vẽ đường thẳng d đi qua A sao cho đường thẳng d cũng đi qua O nếu kéo dài đường thẳng d ra ngoài phạm vi tờ giấy.

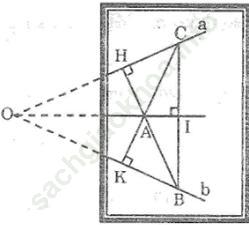
Bài giải:

- Kẻ AH ⊥ a kéo dài HA cắt b tại B

- Kẻ AK ⊥ b kéo dài KA cắt a tại C

- Nối BC

- Kẻ AI ⊥ BC, đường thẳng AI đi qua O

Chứng minh:

Vì tam giác OBC có hai đường cao BH và CK cắt nhau tại A nên A là trực tâm của tam giác OBC.

Khi đó OA là đường cao thứ ba nên OA ⊥ BC.

Lại có: AI ⊥ BC nên đường thẳng OA và đường thẳng AI trùng nhau (vì qua 1 điểm nằm ngoài 1 đường thẳng ta vẽ được một và chỉ một đường thẳng vuông góc với đường thẳng cho trước).

=> đường thẳng AI đi qua O.

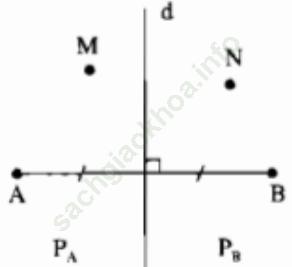
Bài 90 trang 54: Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là P_A, phần chứa điểm B ký hiệu là P_B (hình bên).

a. Gọi M là một điểm của P_A. Chứng minh rằng MA < MB

b. Gọi N là một điểm của P_B. Chứng minh rằng NB < NA

c. Gọi K là một điểm sao cho KA < KB. Hỏi rằng K nằm ở đâu: trong P_A, P_B hay trên d?

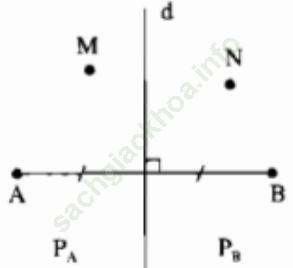
Bài giải:

a. Nối MA, MB. Gọi C là giao điểm của MB với đường thẳng d, nối CA.

Ta có: MB = MC + CB

mà CA = CB (tính chất đường trung trực)

Suy ra: MB = MC + CA (1)

Trong Δ MAC ta có:

MA < MC + CA (bất đẳng thức tam giác) (2)

Từ (1) và (2) suy ra: MA < MB

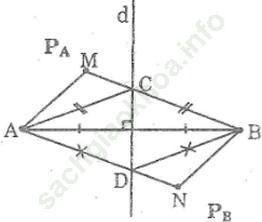
b. Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB.

Ta có: NA = ND + DA

mà DA = DB (tính chất đường trung trực)

Suy ra: NA = ND + DB (3)

Trong Δ NDB, ta có:

NB < ND + DB (bất đẳng thức tam giác) (4)

Từ (3) và (4) suy ra: NA > NB

c) Theo phần a và b; với điểm H bất kì ta có:

+ Nếu H nằm trong phần PA thì HA < HB.

+ Nếu H nằm trong phần PB thì HB < HA.

+ Nếu H nằm trên đường thẳng d thì HA = HB (tính chất đường trung trực)

Do đó, để KA < KB thì K nằm trong phần PA.

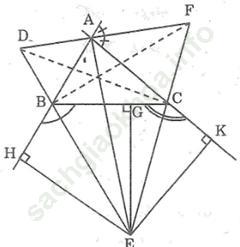
Bài 91 trang 54: Cho tam giác ABC, các đường phân giác của các góc ngoài tại B và C cắt nhau ở E. Gọi G, H, K theo thứ tự là chân đường vuông góc kẻ từ E đến các đường thẳng BC, AB, AC.

a. Có nhận xét gì về các độ dài EH, EG, EK?

b. Chứng minh AE là tia phân giác của góc BAC.

c. Đường phân giác của góc ngoài tại A của tam giác ABC cắt các đường thẳng BE, CE tại D, F. Chứng minh rằng EA vuông góc với DF.

d. Các đường thẳng AE, BF, CD là các đường gì trong tam giác ABC?

e. Các đường thẳng EA, FB, DC là các đường gì trong tam giác DEF?

Bài giải:

a. Ta có: E thuộc tia phân giác của ∠ (CBH)

Suy ra: EG = EH (tính chất tia phân giác) (1)

E thuộc tia phân giác của ∠ (BCK)

Suy ra: EG = EK (tính chất tia phân giác) (2)

Từ (1) và (2) suy ra: EH = EG = EK.

b. Ta có: EH = EK (chứng minh trên)

Suy ra: E thuộc tia phân giác của ∠ (BAC).

Mà E khác A nên AE là tia phân giác của ∠ (BAC)

c. Ta có: AE là tia phân giác góc trong tại đỉnh A

AF là tia phân giác góc ngoài tại đỉnh A

Suy ra: AE ⊥ AF (tính chất hai góc kề bù)

Vậy AE ⊥ DF.

d. Tương tự câu a, ta có:

BF là tia phân giác của ∠ (ABC)

CD là tia phân giác của ∠ (ACB)

Vậy AE, BF, CD là các đường phân giác của tam giác ABC.

e. Ta có: BF là tia phân giác góc trong tại đỉnh B

BE là tia phân giác góc ngoài tại đỉnh B

Suy ra: BF ⊥ BE (tính chất hai góc kề bù)

Vậy BF ⊥ ED.

Lại có: CD là đường phân giác góc ngoài tại C

CE là đường phân giác góc trong tại C

Suy ra: CD ⊥ CE (tính chất hai góc kề bù)

Vậy CD ⊥ EF.

Vậy các đường thẳng EA; FB; DC là các đường cao trong tam giác DEF.

Bài III. 1 trang 54 sách bài tập Toán 7 Tập 2: Chứng minh rằng trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ một đỉnh.

Bài giải:

+) Xét tam giác có đường cao và đường trung tuyến cùng xuất phát từ cùng 1 đỉnh và không trùng nhau:

Vì đường cao và đường trung tuyến xuất phát từ cùng một đỉnh lần lươt là đường vuông góc và đường xiên kẻ từ cùng một điểm đến cùng một đường thẳng.

Do đó, đường cao nhỏ hơn đường trung tuyến (1)

+) Xét tam giác cân có đường cao và đường trung tuyến cùng xuất phát từ đỉnh của tam giác cân nên chúng bằng nhau (2)

Từ (1) và (2) suy ra: trong tam giác cân, đường cao không lớn hơn đường trung tuyến xuất phát từ cùng 1 đỉnh.

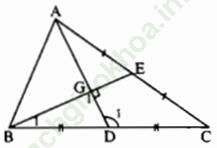
Bài III. 2 trang 54: Cho tam giác ABC có hai đường trung tuyến AD, BE vuông góc với nhau. Chứng minh rằng BC < 2AC.

Bài giải:

Gọi giao điểm của hai đường thẳng AD và BE là G.

+) Xét tam giác BDG có góc ∠ D₁ là góc ngoài tam giác nên:

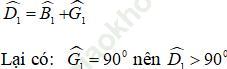
+) Xét tam giác ADC có ∠ D₁ + ∠ A + ∠ C = 180º mà ∠ D₁ > 90º nên ∠ D₁ là góc lớn nhất trong tam giác đó:

=> ∠ D₁ > ∠ A

=> AC > CD (cạnh đối diện với góc lớn hơn thì lớn hơn). (1)

+) Mà D là trung điểm của BC nên

Từ (1) và (2) suy ra:

hay 2AC > BC (điều phải chứng minh)

Bài III. 3 trang 542: Ba đường phân giác AD, BE, CF của tam giác ABC quy đồng tại O. Kẻ đường vuông góc OG đến BC. Chứng minh rằng ∠ (BOG) = ∠ (COD).

Bài giải: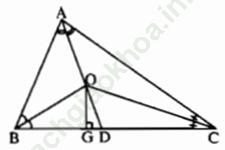

Để chứng minh ∠ (BOG) = ∠ (COD), ta chứng minh ∠ (BOD) = ∠ (GOC).

+) Tổng ba góc trong 1 tam giác bằng 180º nên:

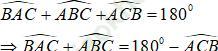
+) Xét tam giác OAB, ta có góc ∠ BOD là góc ngoài tam giác tại đỉnh O nên:

Lại có: BO và AO là tia phân giác của góc B và góc A nên:

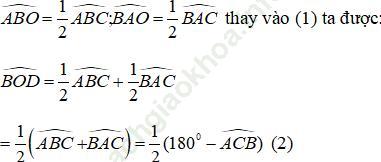
Xét tam giác vuông OCG ta có:

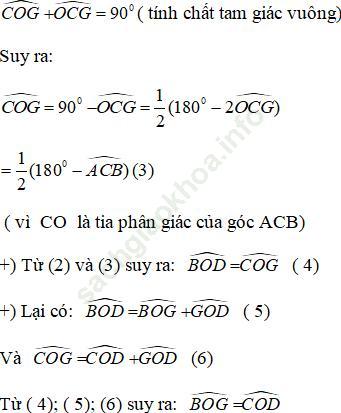
Bài III. 4 trang 54: Cho tam giác ABC cân tại B có ∠ B = 112^o. Kẻ đường cao AH và đường phân giác AD của tam giác đó. Tính các góc của tam giác AHD.

Bài giải: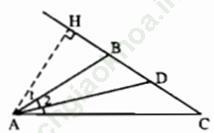

+) Ta có: ∠ (ABH) + ∠ (ABC) = 180º (hai góc kề bù)

=> ∠ (ABH) = 180º - ∠ (ABC) = 180º − 112º = 68º

+) Xét tam giác AHB vuông tại H ta có:

∠A₁+ ∠ (ABH) = 90º (tính chất tam giác vuông)

=> ∠A₁= 90º − ∠ (ABH) = 90º − 68º = 22º

+) Tam giác ABC cân tại B nên ∠ (BAC) = ∠ (ACB)

Lại có ∠ (ABC) = 112º và ∠ (BAC)+ ∠ (ACB) + ∠ (ABC) = 180º nên

∠ (BAC) = (180º − 112º): 2 = 34o

+) Do AD là tia phân giác của góc BAC nên

+ Từ đó

∠ (HAD) = ∠A₁ + ∠A₂= 22º + 17º = 39º.

Tam giác HAD vuông tại H nên: ∠ (HDA)+ ∠ (HAD) = 90º

=> ∠ (HDA) = 90º − ∠ (HAD) = 90º − 39º = 51º.

Bài III. 5 trang 54: Cho tam giác ABC cân tại C. Kẻ các đường cao AA₁ và BB₁ của tam giác đó. Hai đường cao này cắt nhau tại M. Chứng minh rằng đường thẳng MC là đường trung trực của đoạn thẳng AB.

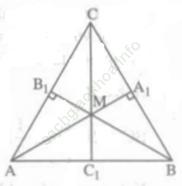
Bài giải:

Gọi giao điểm của CM và AB là C₁. Ta cần chứng minh CC₁ ⊥ AB và C₁ là trung điểm của đoạn thẳng AB. Vì trong một tam giác ba đường cao đồng quy nên CM hay CC₁ vuông góc với AB.

+) Do tam giác ABC cân tại C có CM là đường cao nên CM đồng thời là đường trung trực của đoạn thẳng AB (tính chất tam giác cân).

Bài III. 6 trang 55: Cho tam giác ABC có ∠ A = 130^o. Gọi C', B'là các điểm sao cho AB là đường trung trực của CC' và AC là đường trung trực của BB'. Hai đường thẳng CB' và BC' cắt nhau tại A'. Hãy tìm bên trong tam giác A'BC điểm cách đều ba cạnh của tam giác đó.

Bài giải: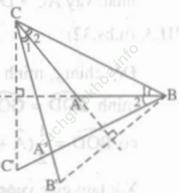

+) Vì AC là đường trung trực của BB'

=> CB’ =CB (tính chất đường trung trực)

Do đó, tam giác CBB’ là tam giác cân tại C. Có CA là đường trung trực của BB’ nên đồng thời là đường phân giác nên có ∠C₁= ∠C₂.

+) Vì AB là đường trung trực của CC' nên BC = BC’.

Suy ra, tam giác BCC’ cân tại B. Lại có BA là đường trung trực nên đồng thời là đường phân giác (tính chất tam giác cân).

=> ∠B₁ = ∠B₂.

+) Ta có: AB, AC lần lượt là đường phân giác của các góc A'BC và góc A'CB; hai đường này cắt nhau tại A.

Vậy ba đường phân giác của tam giác A'BC đồng quy tại A, hay A là điểm nằm trong tam giác A'BC và cách đều ba cạnh của tam giác này.

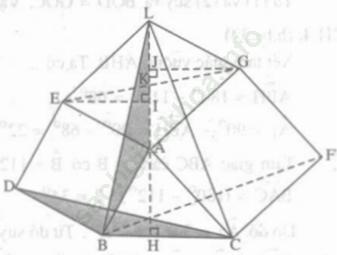
Bài III. 7 trang 55: Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABC cho trước.

a) Gọi H là điểm thuộc đường thẳng BC sao cho AH ⊥ BC. Gọi I, J là các điểm thuộc đường thẳng AH sao cho EI ⊥ AH và GJ ⊥ AH. Chứng minh

Δ ABH = Δ EAI, Δ ACH = Δ GAJ

Từ đó suy ra đường thẳng AH cắt EG tại trung điểm K của EG (tức là AK là trung tuyến của tam giác AEG)

b) Gọi L là điểm thuộc đường thẳng AK sao cho K là trung điểm của AL. Chứng minh AL = BC.

c) Chứng minh Δ ABL = Δ BDC. Từ đó suy ra CD là một đường cao của tam giác BCL.

d) Chứng minh rằng các đường thẳng AH, BF, CD đồng quy.

Bài giải:

a)

+) Xét tam giác EIA vuông tại I nên:

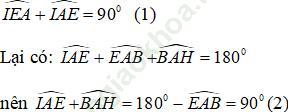
+) Xét hai tam giác ABH và ∆EAI có:

AB = AE (vì ABDE là hình vuông)

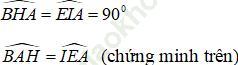
⇒ ∆ABH = ∆ EAI (cạnh huyền – góc nhọn)

⇒ AH = EI (hai cạnh tương ứng)

+) Tương tự hai tam giác vuông ACH và GAJ bằng nhau.

⇒ AH = GJ.

⇒ EI = AH = GJ.

+) Xét ΔEKI và ΔGKJ có:

EI = GJ (chứng minh trên)

∠ (IKE) = ∠ (JKG) (đối đỉnh).

do đó ΔEKI = ΔGKJ (cgv – gn)

⇒ KE = KG

Từ đó ta có K trung điểm của EG. Vậy AK là trung tuyến của tam giác AEG.

b) Theo a) ΔEKI = ΔGKJ nên KI = KJ.

Mặt khác, theo giả thiết K là trung điểm của AL nên KA = KL.

⇒ KA – KI = KL – KJ hay IA= JL.

Ta có: ∆ACH= ∆ GAJ (theo a) nên HC = AJ;

∆ABH = ∆ EAI nên BH = AI.

+) Suy ra:

AL = AJ + JL = AJ + AI = HC + HB = BC

c) Xét tam giác ALB và ∆BCD có:

AL = BC (chứng minh b)

AB = BD (vì ABDE là hình vuông)

∠ (BAL) = 90º + ∠ (EAL) = 90 + ∠ (ABC) = ∠ (DBC).

⇒ ∆ALB = ∆BCD (c. g. c)

⇒ ∠ (ALB) = ∠ (BCD).

Mặt khác ta có ∠ (ALB) + ∠ (LBH) = 90º nên ∠ (BCD) + ∠ (LBH) = 90º.

⇒ LB ⊥ CD, tức CD là một đường cao của tam giác LBC.

d) Lập luận tương tự câu c), ta có BF là một đường cao của tam giác LBC.

Vậy ba đường thẳng AH, BF, CD là ba đường cao của tam giác LBC nên chúng đồng quy.

Bài III. 8 trang 55: Cho tam giác.

a) Qua trung điểm D của cạnh BC, kẻ đường thẳng song song với AB, nó cắt cạnh AC tại E. Qua E kẻ đường thẳng song song với BC, nó cắt AB tại F. Chứng minh Δ CDE = Δ EFA. Từ đó suy ra E là trung điểm của cạnh AC.

b) Chứng minh rằng đường thẳng đi qua các trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba của tam giác đó.

c) Chứng minh rằng tâm đường tròn ngoại tiếp tam giác ABC là trực tâm của tam giác có ba đỉnh là trung điểm ba cạnh của tam giác ABC.

Bài giải: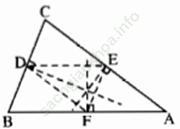

a)

+)Xét tam giác BDF và ∆EFD có:

DF chung

∠ BDF = ∠ DFE (hai góc so le trong; BC// EF)

∠ BFD = ∠ FDE (hai góc so le trong; DE// AB)

Suy ra: ∆ BDF = ∆EFD (g. c. g)

⇒ BD = EF. Theo giả thiết, D là trung điểm của BC nên CD = DB = EF.

+) Xét ∆ CDE và ∆ EFA có:

CD = EF (chứng minh trên)

∠ (CDE) = ∠ (EFA) = ∠ (CBA)

∠ (ECD) = ∠ (AEF) (các góc đồng vị).

⇒ ∆ CDE = ∆ EFA (g. c. g)

⇒ CE = EA nên E là trung điểm của CD.

b) Gọi D là trung điểm của BC, E là trung điểm của AC. Theo câu a)) đường thẳng qua D, song song với AB phải cắt AC tại trung điểm của AC nên đường thẳng đó phải đi qua E, hay DE // AB.

c) Gọi D, E, F theo thứ tự là trung điểm của BC, CA, AB. Đường trung trực của BC phải vuông góc với EF (vì (EF // BC), hay nó là một đường cao của tam giác DEF. Suy ra ba đường trung trực của tam giác ABC là ba đường cao của tam giác DEF. Do đó tâm đường tròn ngoại tiếp tam giác ABC (giao điểm của ba đường trung trực của tam giác ABC) là trực tâm của tam giác DEF.

Bài trước: Bài 9: Tính chất ba đường cao của tam giác - trang 50 sách bài tập Toán 7 Tập 2 Bài tiếp: Ôn tập cuối năm (phần Đại số - phần Hình học) - trang 100 sách bài tập Toán 7 Tập 2