Bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (c.c.c) - trang 140 sách bài tập Toán 7 Tập 1

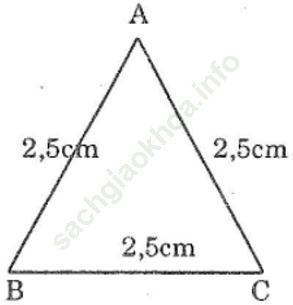
Bài 27 trang 140 sách bài tập Toán 7 Tập 1: Vẽ tam giác ABC biết độ dài mỗi cạnh bằng 2,5cm. Sau đó đo mỗi góc của tam giác.

Bài giải:

Ta có: AB=AC=BC=2,5 cm

Suy ra: Δ ABC đều

Vậy: ∠ A =∠ B =∠ C = 60^o

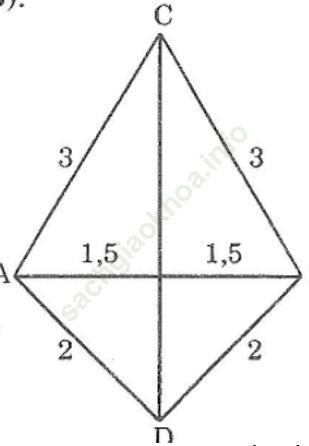
Bài 28 trang 141: Cho hai tam giác ABC và ABD có AB = BC = CA = 3cm, AD = BD = 2cm (C và D nằm khác phía đối với AB)

Chứng minh rằng: ∠ (CAD) =∠ (CBD)

Bài giải:

Xét Δ CAD và Δ CBD, ta có:

AC = BC (= 3 cm)

AD = BD (= 2 cm)

CD cạnh chung

Suy ra: Δ CAD= Δ CBD (c. c. c)

Vậy ∠ (CAD) =∠ (CBD) ̂ (hai góc tương ứng)

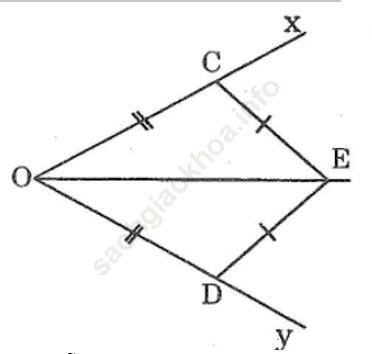
Bài 29 trang 141: Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OD = OC. Vẽ các cung tròn tâm C và tâm D có cùng bán kính sao cho chúng cắt nhau tại E nằm trong xOy. Chứng minh rằng OE là tia phân giác của góc xOy

Bài giải:

Xét Δ COE và Δ DOE. Ta có:

OE cạnh chung

OD = OC (giả thiết)

DE=CE (bán kính 2 cung tròn có bán kính bằng nhau)

Suy ra: Δ COE= Δ DOE (c. c. c)

Vậy: ∠ (COE) =∠ (DOE) (hai góc tương ứng)

Vì điểm E nằm trong góc xOy nên tia OE nằm giữa OC và OD (2)

Từ (1) và (2) suy ra: OE là tia phân giác của góc DOC hay OE là tia phân giác của góc xOy

Bài 30 trang 141: Tìm chỗ sai trong bài làm sau đây của một học sinh (hình bên)

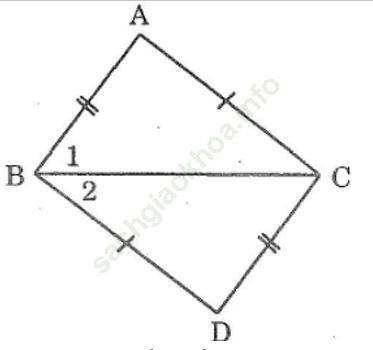
Δ ABC=Δ DCB (c. c. c)

⇒ ∠ (B₁) = ∠ B₂) (cặp góc tương ứng)

⇒ BC là tia phân giác của góc ABD

Bài giải:

Bạn học sinh suy luận Δ ABC = Δ DCB

⇒ ∠ (B₁) = ∠ (B₂) là sai vì ∠ (B₁) và ∠ (B₂) không phải là 2 góc tương ứng của hai tam giác bằng nhau nói trên. Do đó không suy luận ra được BC là tia phân giác của góc ABD

Bài 31 trang 141: Vẽ tam giác ABC có AB = AC = 6cm; BC = 2cm. Sau đó đo góc A để kiểm tra rằng ∠ A ≈ 20^o

Bài giải:

Hình vẽ:

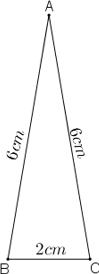
-) Dùng thước dựng đoạn thẳng BC = 2 cm.

-) Dùng compa dựng cung tròn tâm B, bán kính R = 6cm và dựng cung tròn tâm C, bán kính R = 6cm.

Hai cung tròn này cắt nhau tại A. Nối B với A, C với A.

Ta được tam giác ABC thỏa mãn đầu bài.

-) Dùng thước đo độ ta được: ∠A ≈ 20º

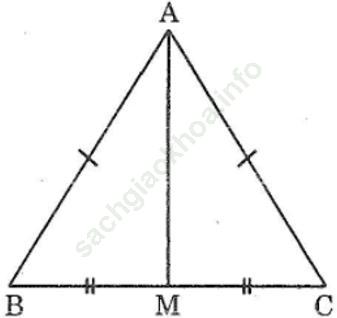
Bài 32 trang 141: Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC.

Bài giải:

Xét Δ AMB và Δ AMC, ta có:

AB = AC (gt)

BM = CM (vì M là trung điểm BC)

AM cạnh chung

Suy ra: Δ AMB= Δ AMC (c. c. c)

⇒ ∠ (AMB) =∠ (AMC) ̂ (hai góc tương ứng)

Ta có: ∠ (AMB) +∠ (AMC) =180^o (hai góc kề bù)

∠ (AMB) =∠ (AMC) =90^o. Vậy AM ⏊ BC

Bài 33 trang 141: Cho đoạn thẳng AB. Vẽ cung tròn tâm A bán kính AB và cung tròn tâm B bán kính BA, chúng cắt nhau ở C và D. Chứng minh rằng:

a, Δ ABC= Δ ABD

b, Δ ACD= Δ BCD

Bài giải: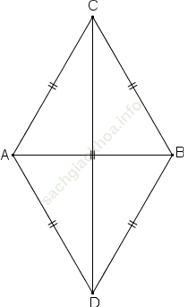

a, Xét Δ ABC và Δ ABD, ta có:

AC = AD (bằng bán kính đường tròn (A))

Ab cạnh chung

BC = BD (bằng bán kính đường tròn (B))

Suy ra: Δ ABC = Δ ABD (c. c. c)

b, Xét Δ ACD và Δ BCD, ta có:

AC = BC (= AB)

CD cạnh chung

AD = BD (= AB)

Suy ra: Δ ACD = Δ BCD (c. c. c)

Bài 34 trang 141: Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán kính BA, chúng cắt nhau tại D (D và B nằm khác phía đối với AC). Chứng minh rằng AD // BC

Bài giải:

Xét Δ ABC và Δ CDA, ta có:

AB = CD (theo cách vẽ)

AC cạnh chung

BC = AD (theo cách vẽ)

Suy ra: Δ ABC = Δ CDA (c. c. c) ⇒ ∠ (ACB) =∠ (CAD) (hai góc tương ứng)

Vậy AD // BC (vì có cặp góc so le trong bằng nhau)

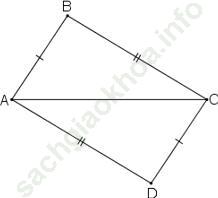
Bài 35 trang 141: Cho đường thẳng xy, các điểm B và C nằm trên xy, điểm A nằm ngoài xy. Dựa vào bài 34, hãy nêu cách vẽ đường thẳng đi qua A và song song với BC.

Bài giải: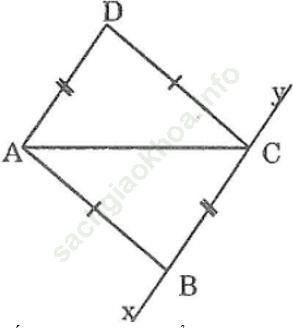

Nối AB, nửa mặt phẳng bờ BC có chứa A. Vẽ cung tròn tâm A bán kính bằng BC. Vẽ cung tròn tâm C bán kính bằng AB. Hai cung tròn cắt nhau tại D.

Kẻ đường thẳng AD ta có AD // xy

Bài 3.1 trang 141 sách bài tập Toán 7 Tập 1: Cho hình bs 1. Điền vào chỗ trống:

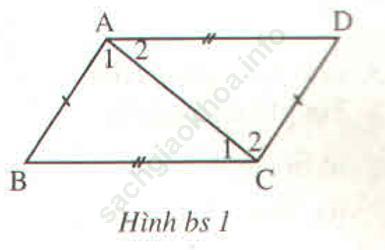
∠ (A₁) = ….

∠ (A₂) = ….

∠ B = …..

Bài giải:

Xét ∆ABC và ∆CDA có:

AB = DC (giả thiết)

BC = DA (giả thiết)

AC chung

Suy ra: ∆ABC và ∆CDA (c. c. c)

Suy ra: các góc tương ứng bằng nhau:

∠ A₁ = ∠ C₂;

∠ A₂ = ∠ C₁;

∠ B = ∠ D.

Bài 3.2 trang 142: Vẽ tam giác ABC có BC = 2cm, AB = AC = 3cm.

b) Gọi E là trung điểm của cạnh BC của tam giác ABC trong câu a). Chứng minh rằng AE là tia phân giác của BAC.

Bài giải: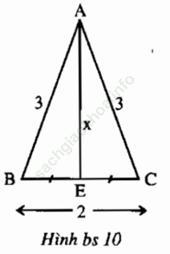

a) Xem hình bs 10.

b) Δ BAE và Δ CAE có:

AB = AC (gt)

BE = EC (E là trung điểm BC)

AE chung.

⇒ Δ BAE = Δ CAE (c. c. c)

⇒ ∠ BAE = ∠ CAE (hai góc t. ư)

Hay AE là phân giác của góc BAC.

Bài 3.3 trang 142: Cho bốn điểm A, B, C, D thuộc đường tròn (O) sao cho AB = CD. Chứng minh rằng ∠ (AOB) = ∠ (COD)

Bài giải: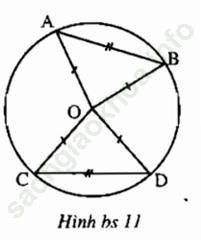

Xét Δ AOB và Δ COD có:

OA = OC (cùng bằng bán kính đường tròn)

OB = OD (cùng bằng bán kính đường tròn)

AB = CD (gt)

⇒ Δ AOB = Δ COD (c. c. c)

⇒ ∠ AOB = ∠ COD (hai góc t. ư)

Bài trước: Bài 2: Hai tam giác bằng nhau - trang 139 sách bài tập Toán 7 Tập 1 Bài tiếp: Bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (c.g.c) - trang 142 sách bài tập Toán 7 Tập 1