Bài 12: Số thực - trang 30 sách bài tập Toán 7 Tập 1
Bài 117 trang 30 sách bài tập Toán 7 Tập 1: Điền các dấu (∈, ∉, ⊂) thích hợp vào ô vuông:
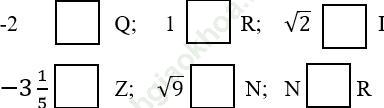
Bài giải:
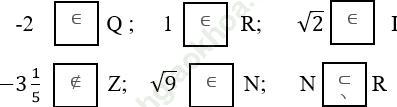
Bài 118 trang 30: So sánh các số thực:
a. 2, (15) và 2, (14)
b. -0,2673 và -0,267 (3)
c. 1, (2357) và 1,2357
d. 0, (428571) và 3/7
Bài giải:a) 2, (15) > 2, (14)
b) -0,267 (3) = - 0,267333... < -0,2673

d) 0, (428571) = 428571.0, (000001)
Bài 119 trang 30: Sắp xếp các số thực sau theo thứ tự từ nhỏ đến lớn:
Bài giải:
Ta có: √ 5 < √ 9 = 3; 22/7 = 3,142857143.. ; π = 3,141592654…
Bài 120 trang 30: Tính bằng cách hợp lý:
A = (-5,85) + {[ (+41,3)+ (+5) + (+0,85))}
B = (-87,5) + {(+87,5) + [(+3,8) + (-0,8)]}
C = [(+9,5) + (-13)] + [(-5) + (8,5)]
Bài giải:A = (-5,85) + {[ (+41,3)+ (+5) + (+0,85))}
= {(-5,85) + [(+5) + (0,85)]} + (+ 41,3)
= {(-5,85) + (5,85)} + (+ 41,3)
= 0 + 41,3
= 41,3
B = (-87,5) + {(+87,5) + [(+3,8) + (-0,8)]}
= [(-87,5) + (+87,5)] + [(+3,8) + (-0,8)]
= 0 + 3 = 3
C = [(+9,5) + (-13)] + [(-5) + (8,5)]
= [(+9,5) + (+8,5)] + [(-5) + (-13)]
= 18 + (-18) = 0
Bài 121 trang 31: Tính:
Bài giải:
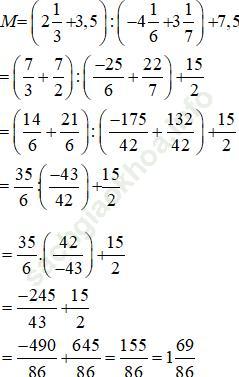
Bài 122 trang 31: Biết rằng:
x + (-4,5) < y + (-4,5)
y + (+6,8) < z + (+6,8)
Hãy sắp xếp các số x, y. z theo thứ tự tăng dần
Bài giải:Vì x + (-4,5) < y + (-4,5) suy ra x < y (1)
y + (+6,8) < z + (+6,8) suy ra y < z (2)
Từ (1) và (2) suy ra: x < y < z
Bài 123 trang 31: Biết rằng:
x – (-3,8) < y – (-3,8)
y – (+ 7,5) < z – (+7,5)
Hãy sắp xếp các số x, y, z theo thứ tự giảm dần
Bài giải:Vì x – (-3,8) < y – (-3,8) suy ra x < y (1)
y – (+ 7,5) < z – (+7,5) suy ra y < z (2)
Từ (1) và (2) suy ra: x < y < z
Bài 124 trang 31: Biết rằng: x + y = 9,8 và x = -3,1. Không tính toán, hãy so sánh x, y và 0
Bài giải:Vì x + y = 9,8 và x = -3,1 nên x < 0 và y > 0
Vậy x < 0 < y
Bài 125 trang 31: Biết rằng: x – y = -5 và y = -6. Không tính toán, hãy so sánh x, y và 0
Bài giải:Vì x – y = -5 < 0 nên x – y < 0, suy ra x < y và y = -6 < 0.
Vậy x < y < 0.
Bài 126 trang 31: Tìm x, biết rằng:
a. 3. (10x) =111
b. 3. (10 + x) =111
c. 3+ (10. x) =111
d. 3 + (10 + x) =111
Bài giải:a. 3. (10x) = 111
10. x = 111: 3
10. x = 37
x = 37: 10
x = 3,7
b. 3. (10 + x) = 111
10+ x = 111: 3
10 + x = 37
x = 37 – 10
x = 27
c. 3 + (10. x) = 111
10. x = 111- 3
10. x = 108
x = 108: 10
x = 10,8
d. 3 + (10 + x) = 111
10 + x = 111- 3
10 + x = 108
x = 108 – 10
x = 98
Bài 127 trang 31: Tìm x, y, z trong các trường hợp sau đây, bạn sẽ thấy điều kì lạ:
a. 5. x = 6,25; 5 + x = 6,25
b. (3/4).y= -2,25; (3/4) + y = -2,25
c. 0,95. z = -18,05; 0,95 + z = -18,05
Bài giải:a) 5. x = 6,25
x = 6,25: 5
x = 1,25
và 5 + x = 6,25
x = 6,25 – 5
x = 1,25
b) (3/4).y = -2,25
y = -2,25: (3/4)
y = -2,25: 0,75
y = -3
Và (3/4) + y = -2,25
y = -2,25 - (3/4)
y = -2,25 - 0,75
y = -3
c) 0,95. z = -18,05
z = -18,05: 0,95
z = -19
và 0,95 + z = -18,05
z = -18,05 – 0,95
z = -19
Điều đặc biệt: Các cặp số 5 và 1,25; 3/4 và -3; 0,95 và -19 có tổng bằng tích.
Bài 128 trang 31: Tính:
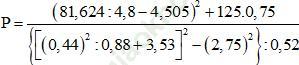
Bài giải:
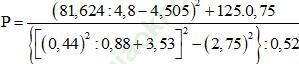
Tử số: (81,624: 4,8 – 4,505)2 + 125.0,75
= (17,005 – 4,505)2 + 93,75
= (12,5)2 + 93,75
= 156,25 + 93,75 = 250
Mẫu số: { [(0,44)2: 0,88 + 3,53]2 – (2,75)2}: 0,52
= [(0,22 + 3,53)2 – (2,75)2]: 0,52
= [(3,75)2 – (2,75)2]: 0,52
= (14,0625 – 7,5625): 0,52
= 6,5: 0,52 = 12,5.
Vậy ![]()
Bài 129 trang 31: Mỗi biểu thức X, Y, Z sau đây được cho 3 giá trị A, B, C trong đó chỉ có một giá trị đúng. Hãy chọn giá trị đúng ấy:
a. X = √ 144
A. 72 B. 12 C. -12
A. 5-3 B. 8 C. 4
A. 2 + 6 + 9 B. ± 11 C. 11
Bài giải: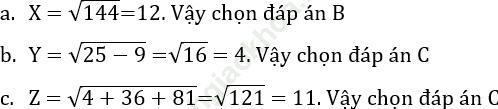
Bài 12.1 trang 32 sách bài tập Toán 7 Tập 1: Điền dấu x vào ô thích hợp trong bảng sau:
| Câu | Đúng | Sai |
| a) a là số vô tỉ thì a cũng là số thực | ||
| b) a là căn bậc hai của một số tự nhiên thì a là số vô tỉ | ||
| c) a là số thực thì a là số vô tỉ | ||
| d) a là số hữu tỉ thì a không phải là số vô tỉ |
Bài giải:
| a) Đúng; | b) Sai; | c) Sai; | d) Đúng. |
Bài 12.2 trang 32: Tìm khẳng định đúng trong các khẳng định sau:
(A) Tổng của hai số vô tỉ là một số vô tỉ.
(B) Tích của hai số vô tỉ là một số vô tỉ.
(C) Tổng của một số hữu tỉ và một số vô tỉ là một số vô tỉ.
(D) Thương của hai số vô tỉ là một số vô tỉ.
Bài giải:Đáp án đúng là (C) Tổng của một số hữu tỉ và một số vô tỉ là một số vô tỉ.
Bài 12.3 trang 32: Thương của một số vô tỉ và một số hữu tỉ là một số vô tỉ hay số hữu tỉ?
Bài giải:Gọi a là số vô tỉ, b là số hữu tỉ.
Ta có a/b là số vô tỉ vì ngược lại nếu a/b = b' là số hữu tỉ thì a = b. b'
Khi đó, b là số hữu tỉ và b’là số hữu tỉ nên a là số hữu tỉ (tích của hai số hữu tỉ là số hữu tỉ); trái với giả thiết a là số vô tỉ.
Như vậy, thương của một số vô tỉ và một số hữu tỉ là số vô tỉ.
Bài 12.4 trang 32: Tích của một số vô tỉ và một số hữu tỉ là một số vô tỉ hay hữu tỉ?
Bài giải:Gọi a là số vô tỉ, b là số hữu tỉ khác 0.
Tích ab là số vô tỉ vì nếu ab = b' là số hữu tỉ thì a = b'/b là thương của hai số hữu tỉ
suy ra a là số hữu tỉ, mâu thuẫn với a là số vô tỉ.
Vậy, tích của một số vô tỉ và một số hữu tỉ khác 0 là một số vô tỉ.
Bài 12.5 trang 32: Cho x > y > 0. Chứng minh rằng x3 > y3.
Bài giải:*) Từ x > y > 0 ta có:
x > y ⇒ xy > y2 (1)
x > y ⇒ x2 > xy (2)
*) Từ (1) và (2) suy ra x2 > y2.
x2 > y2 ⇒ x3 > xy2 (3)
x > y ⇒ xy2 > y3 (4)
Từ (3) và (4) suy ra x3 > y3.
Bài 12.6 trang 32: Chứng minh rằng nếu số tự nhiên a không phải là số chính phương thì √a là số vô tỉ.
Bài giải:Giả sử √ a là số hữu tỉ thì √ a viết được thành √ a = m/n với m, n ∈ N, (n ≠ 0) và ƯCLN (m, n) = 1
Do a không phải là số chính phương nên m/n không phải là số tự nhiên, do đó n > 1.
Gọi p là một ước nguyên tố của n thì m2 ⋮ p, do đó m ⋮ p. Như vậy p là ước nguyên tố của m và n, trái với giả thiết ƯCLN (m, n) = 1. Vậy √ a là số vô tỉ.