Bài 4: Số trung bình cộng - trang 10 sách bài tập Toán 7 Tập 2
Bài 11 trang 10 sách bài tập Toán 7 Tập 2: Tính số trung bình cộng và tìm mốt của dãy giá trị sau bằng cách lập bảng:
| 17 | 20 | 18 | 18 | 19 | 17 | 22 | 30 | 18 | 21 |
| 17 | 32 | 19 | 20 | 26 | 18 | 21 | 24 | 29 | 21 |
| 28 | 18 | 19 | 31 | 26 | 26 | 31 | 24 | 24 | 22 |
| Giá trị (x) | Tần số (n) | Các tích (x. n) | |
| 17 | 3 | 51 | |
| 18 | 5 | 90 | |
| 19 | 4 | 76 | |
| 20 | 2 | 40 | |
| 21 | 3 | 63 | |
| 22 | 2 | 44 | |
| 24 | 3 | 72 | |
| 26 | 3 | 78 | |
| 28 | 1 | 28 | |
| 30 | 1 | 30 | |
| 31 | 2 | 62 | |
| 32 | 1 | 32 | |
| N = 30 | Tổng: 666 |
Giá trị 18 có tần số lớn nhất nên mốt của dấu hiệu là: M0 = 18
Bài 12 trang 10: Theo dõi nhiệt độ trung bình hàng năm của hai thành phố A và B từ năm 1956 đến năm 1975 (đo theo độ C) người ta lập được các bảng sau:
* Đối với thành phố A
| Nhiệt độ trung bình (x) | 23 | 24 | 25 | 26 | |
| Tần số (n) | 5 | 12 | 2 | 1 | N = 20 |
* Đối với thành phố B
| Nhiệt độ trung bình (x) | 23 | 24 | 25 | |
| Tần số (n) | 7 | 10 | 3 | N = 20 |
Hãy so sánh nhiệt độ trung bình hàng năm giữa hai thành phố
Bài giải:* Nhiệt độ trung bình của thành phố A:
| Giá trị (x) | Tần số (n) | Các tích (x. n) | |
| 23 | 5 | 115 | |
| 24 | 12 | 288 | |
| 25 | 2 | 50 | |
| 26 | 1 | 26 | |
| N = 20 | Tổng: 479 |
|
* Nhiệt độ trung bình của thành phố B:
| Giá trị (x) | Tần số (n) | Các tích (x. n) | |
| 23 | 7 | 161 | |
| 24 | 10 | 240 | |
| 25 | 3 | 75 | |
| N = 20 | Tổng: 476 |
|
Nhiệt độ trung bình hàng năm của thành phố A cao hơn thành phố B.
Bài 13 trang 10: Hai xạ thủ A và B cùng bắn 20 phát đạn, kết quả ghi lại được dưới đây:

a. Tính điểm trung bình của từng xạ thủ
b. Có nhận xét gì về kết quả và khả năng của từng người.
Bài giải:* Điểm trung bình của xạ thủ A
| Giá trị (x) | Tần số (n) | Các tích (x. n) | |
| 8 | 5 | 40 | |
| 9 | 6 | 54 | |
| 10 | 9 | 90 | |
| N = 20 | Tổng: 184 |
|
* Điểm trung bình của xạ thủ B
| Giá trị (x) | Tần số (n) | Các tích (x. n) | |
| 6 | 2 | 12 | |
| 7 | 1 | 7 | |
| 9 | 5 | 45 | |
| 10 | 12 | 120 | |
| N = 20 | Tổng: 184 |
|
b) Nhận xét:
+ Điểm trung bình của hai xạ thủ như nhau nên khả năng của họ là như nhau.
+ Tuy nhiên nhìn kết quả có thể thấy xạ thủ A có phong độ ổn định hơn.
Bài 4.1 trang 11 sách bài tập Toán 7 Tập 2: Tổng số áo sơ mi mà một cửa hàng bán trong một ngày được thống kê lại trong bảng sau:
| Cỡ áo | 37 | 38 | 39 | 40 | 41 |
| Số áo bán được | 4 | 7 | 10 | 3 | 1 |
a) Số áo bán được là bao nhiêu?
b) Mốt của dấu hiệu là:
(A) 41;
(B) 10;
(C) 39;
(D) 25.
Hãy chọn phương án đúng.
Bài giải:a) Số áo bán được là:
4 + 7 + 10 +3 +1 = 25 (cái áo).
b) Cỡ áo 39 bán được nhiều nhất là 10 cái. Nên mốt của dấu hiệu là: M0 = 39
Đáp án đúng là C.
Bài 4.2 trang 11: Mật độ dân số của một số tỉnh, thành phố ở nước ta năm 2008 được cho trong bảng sau:
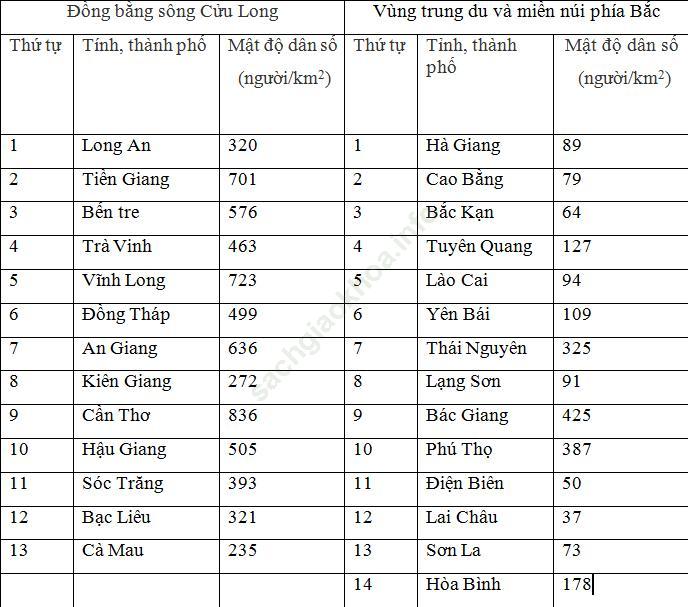
Mật độ dân số của một địa phương được tính bằng cách: Lấy tổng số dân trung bình của địa phương đó (tại một thời điểm nhất định) chia cho diện tích của chính địa phương ấy (người/km2).
a) Dấu hiệu ở đây là gì?
b) Nhận xét chung về mật độ dân số ở hai vùng
c) Tính mật độ dân số của từng vùng và so sánh.
Bài giải:a) Dấu hiệu là: Mật độ dân số của một tỉnh, thành phố.
b) - Mật độ dân số vùng Đồng bằng sông Cửu Long nói chung cao hơn so so với vùng Trung du và miền núi phía Bắc.
- Mật độ dân số của vùng Trung du và miền núi phía Bắc: 152 (người/km2). Rõ ràng là mật độ dân số ở đồng bằng sông cửu Long cao hơn vùng Trung du và miền núi phía Bắc.
c)
- Tổng mật độ dân số của đồng bằng sông Cửu Long là:
320+ 701 +576 + 463+ 723+ 499+ 636+ 272+ 836+ 505+ 393+ 321+ 235
= 6480 (người/ km2)
Mật độ dân số trung bình của đồng bằng sông Cửu Long là:
6480: 13 ≈ 498 (người / km2).
- Tổng mật độ dân số của vùng trung du và miền núi phía Bắc là:
89 +79 + 64 +127 +94 + 109 +325+ 91+425+ 387+ 50+ 37+ 73+ 178
= 2128 (người/ km2)
Mật độ dân số trung bình của vùng trung du và miền núi phía Bắc là:
2128: 14 = 152 (người / km2).
* Nhận xét: mật độ dân số ở đồng bằng sông cửu Long cao hơn vùng Trung du và miền núi phía Bắc.
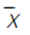 = 479/20 = 23,95oC
= 479/20 = 23,95oC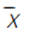 = 476/20 = 23,8oC
= 476/20 = 23,8oC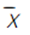 = 184/20 = 9,2
= 184/20 = 9,2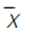 = 184/20 = 9,2
= 184/20 = 9,2