Bài 4: Tính chất ba đường trung tuyến của tam giác - trang 42 sách bài tập Toán 7 Tập 2

Bài 31 trang 42 sách bài tập Toán 7 Tập 2: Cho hình dưới. Điền vào chỗ trống:

GK = … CK; AG = … GM; GK = … CG; AM = … AG; AM = … GM

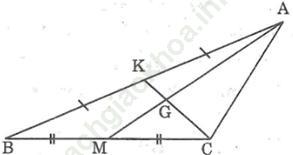
Bài giải:

Theo hình vẽ ta có: AM và CK là hai đường trung tuyến của tam giác ABC. Hai đường trung tuyến này cắt nhau tại G nên G là trọng tâm tam giác ABC.

Áp dụng tính chất trọng tâm tam giác ta có:

GK = 1/3 CK; AG = 2GM; GK = 1/2 CG; AM = 3/2 AG; AM = 3GM

Bài 32 trang 42: Chứng minh rằng nếu một tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân.

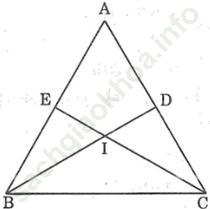
Bài giải:

Giả sử Δ ABC có hai đường trung tuyến BD và CE bằng nhau.

Gọi I là giao điểm BD và CE, ta có:

BI = 2/3 BD (tính chất đường trung tuyến) (1)

CI = 2/3 CE (tính chất đường trung tuyến) (2)

Từ (1), (2) và giả thiết BD = CE suy ra: BI = CI

Do BD = CE suy ra: BI + ID = CI + IE

Mà BI = CI (chứng minh trên) nên: ID = IE

Xét Δ BIE và Δ CID, ta có:

BI = CI (chứng minh trên)

∠ (BIE) = ∠ (CID) (đối đỉnh)

IE = ID (chứng minh trên)

Suy ra: Δ BIE = Δ CID (c. g. c)

Suy ra: BE = CD (hai cạnh tương ứng) (3)

Lại có: BE = 1/2 AB (vì E là trung điểm AB) (4)

CD = 1/2 AC (vì D trung điểm AC) (5)

Từ (3), (4) và (5) suy ra: AB = AC.

Vậy tam giác ABC cân tại A.

Bài 33 trang 42: Tam giác ABC cân tại A có AB = AC = 34cm, BC = 32cm. Kẻ đường trung tuyến AM.

a. Chứng minh rằng AM ⊥ BC.

b. Tính độ dài AM

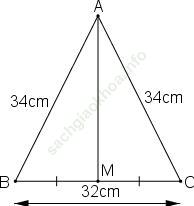
Bài giải:

a. Xét Δ AMB và Δ AMC, ta có:

AB = AC (gt)

BM = CM (vì M là trung điểm BC)

AM cạnh chung

Suy ra: Δ AMB = Δ AMC (c. c. c)

Suy ra: ∠ (AMB) = ∠ (AMC) (1)

Lại có: ∠ (AMB) + ∠ (AMC) = 180^o (hai góc kề bù) (2)

Từ (1) và (2) suy ra: ∠ (AMB) = ∠ (AMC) = 90^o

Vậy AM ⊥ BC.

b. Do M là trung điểm của BC nên BM = CM = BC/2 cm

Tam giác AMB có ∠ (AMB) = 90^o

Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:

AB² = AM² + BM² ⇒ AM² = AB² - BM² = 34² - 16²

= 1156 - 256 = 900

Suy ra: AM = 30 (cm).

Bài 34 trang 42: Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng:

a. Các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

b. Các đường trung tuyến của tam giá BGD bằng một nửa các cạnh của tam giác ABC.

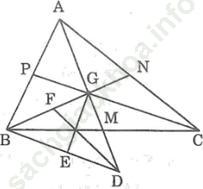
Bài giải:

a. Gọi AM, BN, CP lần lượt là các đường trung tuyến của Δ ABC. Các đường trung tuyến cắt nhau tại G.

Ta có: AG = GD (gt)

AG = 2GM (tính chất đường trung tuyến)

Suy ra: GD = 2GM

Mà GD = GM + MD ⇒ GM = MD

Xét Δ BMD và Δ CMG, ta có:

BM = CM (gt)

∠ (BMD) = ∠ (CMG) (đối đỉnh)

MD = GM (chứng minh trên)

Suy ra: Δ BMD = Δ CMG (c. g. c)

⇒ BD = CG (hai cạnh tương ứng)

Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)

Suy ra: BD = 2/3 CP (1)

Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)

Và AG = 2/3 AM (tính chất đường trung tuyến)

Suy ra: GD = 2/3 AM (3)

Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

b. Ta có: GM = MD (chứng minh trên)

Suy ra BM là đường trung tuyến của tam giác BGD.

Suy ra: BM = 1/2 BC (4)

Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:

FG = 1/2 BG (tính chất đường trung tuyến)

GN = 1/2 GB (tính chất đường trung tuyến)

Suy ra: FG = GN

Xét Δ DFG và Δ ANG, ta có:

AG = GD (gt)

∠ (DGF) = ∠ (AGN) (đối đỉnh)

GF = GN (chứng minh trên)

Suy ra: Δ DFG = Δ ANG (c. g. c) ⇒ DF = AN

Mà AN = 1/2 AC (gt)

Suy ra: DF = 1/2 AC (5)

Mặt khác: BD = CG (chứng minh trên)

ED = 1/2 BD (vì E là trung điểm BD)

GP = 1/2 CG (tính chất đường trung tuyến)

Suy ra: ED = GP

Lại có: Δ BMD = Δ CMG (chứng minh trên)

⇒ ∠ (BDM) = ∠ (CGM) hay ∠ (EDG) = ∠ (CGM)

(CGM) = (PGA) (đối đỉnh)

Suy ra: ∠ (EDG) = ∠ (PGA)

AG = GD (gt)

Suy ra: Δ PGA = Δ EDG (c. g. c) ⇒ GE = AP mà AP = 1/2 AB (gt)

Do đó: GE = 1/2 AB (6)

Từ (4), (5) và (6) suy ra các đường trung tuyến của Δ BGD bằng một nửa cạnh của Δ ABC.

Bài 35 trang 42: Tam giác ABC có BC = 10cm, các đường trung tuyến BD và CE. Chứng minh rằng BD + CE > 15cm.

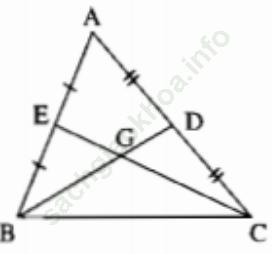
Bài giải:

Gọi G là giao điểm của BD và CE.

Trong ∆GBC, ta có:

GB + GC > BC (bất đẳng thức tam giác)

GB = 2/3 BD (tính chất đường trung tuyến)

GC = 2/3 CE (tính chất đường trung tuyến)

Mà BC = 10 cm (gt)

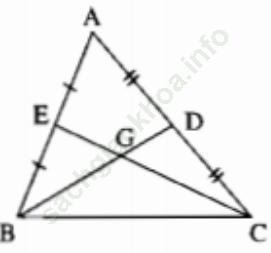
⇒ BD + CE > 15 (cm).

Bài 36 trang 43: Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho BE = 1/3 BC. Gọi K là giao điểm của AE và CD. Chứng minh rằng DK = KC.

Bài giải: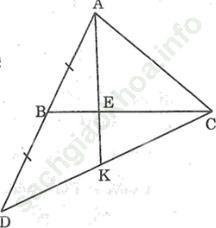

Trong Δ ACD ta có:

CB là đường trung tuyến kẻ từ đỉnh C

Mặt khác:

E ∈ BC và BE = 1/3 BC (gt)

Nên: CE = 2/3 CB

Suy ra: E là trọng tâm của Δ ACD.

Vì AK đi qua E nên AK là đường trung tuyến của Δ ACD

Suy ra K là trung điểm của CD

Vậy KD = KC.

Bài 37 trang 43: Theo kết quả của bài 64 chương II, sách Bài tập toán 7 tập một ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Vận dụng kết quả trên để giải bài toán sau: Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng:

a. IK // DE, IK = DE

b. AG = 2/3 AD

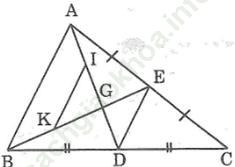
Bài giải:

a. Áp dụng kết quả bài 64 chương II sách Bài tập toán 7 vào Δ ABC và Δ AGB ta có:

DE // AB và DE = 1/2 AB (1)

IK // AB và IK = 1/2 AB (2)

Từ (1) và (2) suy ra:

DE // IK và DE = IK.

b. Vì AD và BE là 2 đường trung tuyến của Δ ABC cắt nhau tại G nên theo tính chất đường trung tuyến, ta có: AG = 2/3 AD.

Bài 38 trang 43: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.

a. Tính số đo góc ABD.

b. Chứng minh Δ ABC = Δ BAD

c. So sánh độ dài AM và BC.

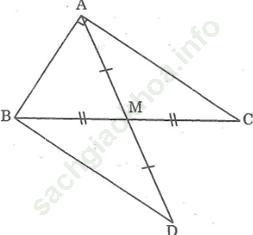
Bài giải:

a. Xét Δ AMC và Δ DMB, ta có:

CM = BM (gt)

∠ (AMC) = ∠ (BMD) (đối đỉnh)

AM = MD (gt)

Suy ra: Δ AMC = Δ DMB (c. g. c)

⇒ ∠ (MAC) = ∠ D (2 góc tương ứng)

Suy ra: AC // BD

(vì có 2 góc ở vị trí so le trong bằng nhau)

Mà AB ⊥ AC (gt) nên AB ⊥ BD.

Vậy ∠ (ABD) = 90^o.

b. Xét Δ ABC và Δ BAD ta có:

AB cạnh chung

∠ (BAC) = ∠ (ABD) = 90^o

AC = BD (vì Δ AMC = Δ DMB)

Suy ra: Δ ABC = Δ BAD (c. g. c)

c. Ta có: Δ ABC = Δ BAD ⇒ BC = AD (2 cạnh tương ứng)

Mặt khác: AM = 1/2 AD

Vậy AM = 1/2 BC.

Bài 39 trang 43: Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng ∠ (BAC) = 90^o

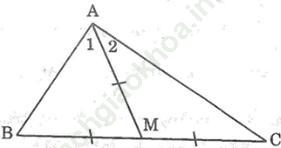
Bài giải:

Vì AM là đường trung tuyến của Δ ABC nên BM = MC = 1/2 BC

Mà AM = 1/2 BC (gt) nên: AM = BM = MC.

Tam giác AMB có AM = MB nên Δ AMB cân tại M

Suy ra: ∠ B = ∠ A₁ (tính chất tam giác cân) (1)

Tam giác AMC có AM = MC nên Δ AMC cân tại M

Suy ra: ∠ C = ∠ A₂ (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: ∠ B + ∠ C = ∠ A₁ + ∠ A₂ = ∠ (BAC) (3)

Trong Δ ABC ta có:

∠ B + ∠ C + ∠ (BAC) = 180^o (tổng ba góc trong tam giác) (4)

Từ (3) và (4) suy ra: ∠ (BAC) + ∠ (BAC) = 180^o ⇔ 2∠ (BAC) = 180^o

Hay ∠ (BAC) = 90^o.

Vậy Δ ABC vuông tại A.

Bài 4.1 trang 43 sách bài tập Toán 7 Tập 2: Cho tam giác ABC. Trên đường trung tuyến AM của tam giác đó, lấy hai điểm D, E sao cho AD = DE = EM. Gọi O là trung điểm của đoạn thẳng DE. Khi đó trọng tâm của tam giác ABC là:

(A) Điểm D

(B) Điểm E

(C) Điểm O

(D) Cả (A), (B), (C) đều sai

Bài giải:

Trên đường trung tuyến AM có AD = DE = EM nên AE = 2/3 AM.

Do khoảng cách từ trọng tâm tới một đỉnh của tam giác bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó nên E là trọng tâm của tam giác ABC. Chọn (B) Điểm E.

Bài 4.2 trang 43: Cho tam giác ABC, trên đường trung tuyến AD. Gọi G là điểm nằm giữa A và D sao cho AG/AD = 2/3. Tia BG cắt AC tại E, tia CG cắt AB tại F. Khẳng định nào sau đây sai?

(A) BG/EG = 2

(B) FG/CG = 2/3

(C) E là trung điểm của cạnh AC

(D) F là trung điểm của cạnh AB

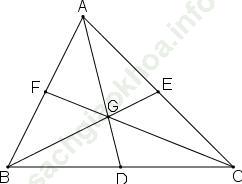
Bài giải:

Trên đường trung tuyến AD có điểm G thỏa mãn:

Suy ra: G là trọng tâm tam giác ABC.

Do tia BG cắt AC tại E nên E là trung điểm của AC.

Do tia CG cắt AB tại F nên F là trung điểm của AB.

Theo tính chất trọng tâm tam giác ta có:

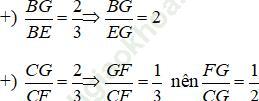
Chọn (B)

Bài 4.3 trang 44: Hai đoạn thẳng AB và CD cắt nhau tại trung điểm của mỗi đoạn. Gọi E và F theo thứ tự là trung điểm của các đoạn thẳng AD và BD. Các đoạn thẳng CE và CF lần lượt cắt đoạn thẳng AB tại I, J. Chứng minh rằng: AI = IJ = JB

Bài giải: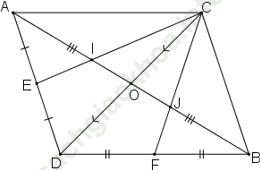

Gọi O là giao điểm của hai đoạn thẳng AB và CD.

⇒ AO = OB và CO = OD.

+ Δ ACD có trung tuyến AO, CE cắt nhau tại I

⇒ I là trọng tâm Δ ACD

⇒ AI = 2/3. AO = 2/3.1/2. AB = 1/3. AB

+ Tương tự J là trọng tâm Δ BCD

⇒ BJ = 2/3. BO = 2/3.1/2. BA = 1/3. AB

⇒ IJ = AB – AI – BJ = 1/3. AB

Vậy AI = IJ = JB

Bài 4.4 trang 44: Trong tam giác ABC, hai đường trung tuyến AA₁và BB_1 cắt nhau tại điểm O. Hãy tính diện tích tam giác ABC nếu diện tích tam giác ABO bằng 5cm².

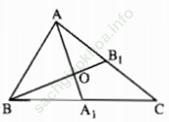
Bài giải:

+) Vì tam giác ABC có hai đường trung tuyến AA₁ và BB₁ cắt nhau tại O nên O là trọng tâm tam giác ABC.

Theo tính chất trọng tâm tam giác ta có:

+) Ta có:

( vì có cùng chiều cao hạ từ B và

)

Và

(vì có cùng chiều cao hạ từ A và ).

+) Từ đó suy ra:

Nếu S_AOB = 5cm² thì S_ABC = 3.5 = 15 (cm²)

Bài 4.5 trang 44: Chứng minh rằng các trung tuyến của một tam giác phân chia tam giác đó thành 6 tam giác mà diện tích của chúng (đôi một) bằng nhau.

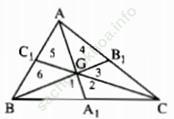
Bài giải:

Xét sáu tam giác được đánh số là: 1,2,3,4,5,6

Chứng minh hoàn toàn tương tự như bài 4.4 ta có

S_GAB = S_GBC = S_GCA = 1/3 S_ABC

Ta lại có S₁ = S₂, S₃ = S₄, S₅ = S₆ (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau, vậy sáu tam giác 1,2,3,4,5,6 có diện tích bằng nhau)

Bài 4.6 trang 44: Cho tam giác ABC với đường trung tuyến AD. Trên tia AD lấy điểm E sao cho AD = DE, trên tia BC lấy điểm M sao cho BC = CM.

a) Tìm trọng tâm của tam giác AEM.

b) So sánh các cạnh của tam giác ABC với các đường trung tuyến của tam giác AEM

c) So sánh các đường trung tuyến của tam giác ABC với các cạnh của tam giác AEM.

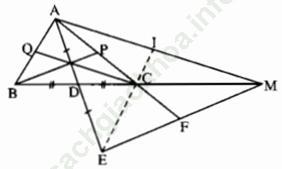
Bài giải:

a) Do AD = DE nên MD là một đường trung tuyến của tam giác AEM. Hơn nữa do

CD = 1/2 CB = 1/2 CM

Nên C là trọng tâm của tam giá AEM.

b) Các đường thẳng AC, EC lần lượt cắt EM, AM tại F, I. Tam giác AEM có các đường trung tuyến là AF, EI, MD. Ta có Δ ADB = Δ EDC (c. g. c) nên AB = EC

Vậy: AC = 2/3 AF; BC = CM = 2/3 MD; AB = EC = 2/3 EI

c) Trước tiên, theo giả thiết, ta có AD = DE nên AD = 1/2 AE

Gọi BP, CQ là các trung tuyến của Δ ABC.

Δ BCP = Δ MCF (c. g. c) ⇒ BP = FM = 1/2 EM. Ta sẽ chứng minh CQ = 1/2 AM

Ta có:

ΔABD = ΔECD (c. g. c) ⇒ ∠ (BAD) = ∠ (CED)

⇒ AB//EC (vì có cặp góc so le trong bằng nhau). ⇒ ∠ (QAC) = ∠ (ICA) (hai góc so le trong)

Hai tam giác ACQ và CAI có

Cạnh AC chung

∠ (QAC) = ∠ (ICA) (Chứng minh trên);

AQ = 1/2 AB = 1/2 EC = IC

Suy ra: ∆ ACQ = ∆ CAI (c. g. c)

Vậy CQ = AI = 1/2 AM.

Tóm lại: AD = 1/2 AE, BP = 1/2 EM, CQ = 1/2 AM.

Bài trước: Bài 3: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác - trang 40 sách bài tập Toán 7 Tập 2 Bài tiếp: Bài 5: Tính chất tia phân giác của một góc - trang 44 sách bài tập Toán 7 Tập 2