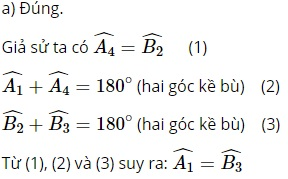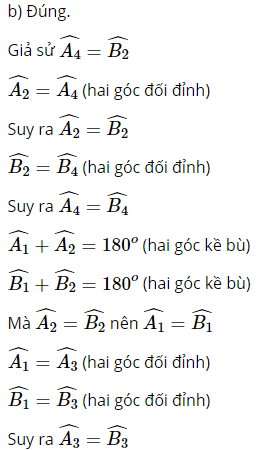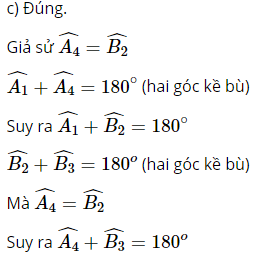Bài 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng - trang 103 sách bài tập Toán 7 Tập 1

Bài 16 trang 103 sách bài tập Toán 7 Tập 1: Vẽ hình và giới thiệu

- Hai cặp góc so le trong

- Bốn cặp góc đồng vị

- Hai cặp góc so le ngoài

- Hai cặp góc trong cùng phía

- Hai cặp góc ngoài cùng phía

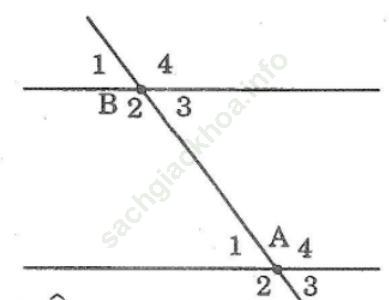
Bài giải:

Hai cặp góc so le trong: ∠ (A₁)và ∠ (B₃); ∠ (A₄) và ∠ (B₂)

Bốn cặp góc đồng vị: ∠ (A₁) và ∠ (B₁); ∠ (A₂) và ∠ (B₂); ∠ (A₃) và ∠ (B₃); ∠ (A₄) và ∠ (B₄)

Hai cặp góc so le ngoài: ∠ (A₃) và ∠ (B₁); ∠ (A₂) và ∠ (B₄);

Hai cặp góc trong cùng phía: ∠ (A₁) và ∠ (B₂); ∠ (A₄) và ∠ (B₃);

Hai cặp góc ngoài cùng phía: ∠ (A₂) và ∠ (B₁); ∠ (A₃) và ∠ (B₄)

Bài 17 trang 104: Vẽ lại hình dưới rồi điền tiếp số đo của các góc còn lại

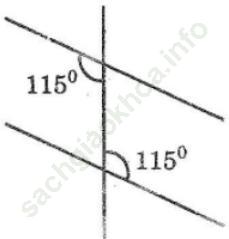
Bài giải:

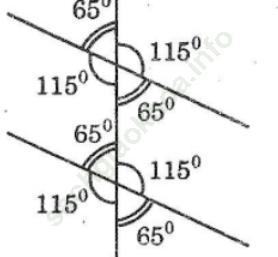
Bài 18 trang 104:

a) Vẽ một đường thẳng cắt hai đường thẳng. Trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.

b, Vì sao cặp góc so le trong còn lại cũng bằng nhau?

c, Vì sao mỗi cặp góc đồng vị bằng nhau

d, Vì sao mỗi cặp góc trong cùng phía bù nhau

e, Vì sao mỗi cặp góc ngoài cùng phía bù nhau

Bài giải:

a. Ta có hình vẽ như sau:

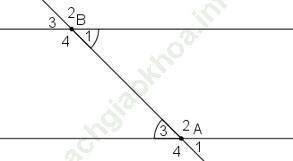
b. Giả sử hai cặp góc so le trong bằng nhau là A₃ và B₁, ta cần chứng minh cặp góc so le trong còn lại ∠ A₂ = ∠ B₄.

Ta có: ∠ (A₂) + ∠ (A₃) = 180^o (hai góc kề bù)

∠ (B₁) + ∠ (B₄) = 180^o (hai góc kề bù)

Suy ra ∠ (A₂) + ∠ (A₃) = ∠ (B₁) + ∠ (B₄)

Mà ∠ A₃ = ∠ B₁

Suy ra ∠ (A₂) = ∠ (B₄)

c. ∠ (B₁) = ∠ (B₃) (hai góc đối đỉnh)

Mà ∠ (B₁) = ∠ (A₃) (giả thiết)

⇒ ∠ (A₃) = ∠ (B₃)

Chứng minh tương tự ta được:

∠ (A₁) = ∠ (B₁)

∠ (A₂) = ∠ (B₂)

∠ (A₄) = ∠ (B₄)

d. Có ∠ (A₃) = ∠ (B₁)

Mà ∠ (A₂) + ∠ (A₃) = 180^o (hai góc kề bù)

Suy ra: ∠ (A₂) + ∠ (B₁) = 180^o.

Vậy hai góc trong cùng phía A₂ và B₁ bù nhau.

Chứng minh tương tự có ∠ A₃ và ∠ B₄ bù nhau.

e. ∠ (B₁) = ∠ (A₁) (hai góc đồng vị bằng nhau ở phần b).

∠ (B₁) + ∠ (B₂) = 180^o (hai góc kề bù).

Suy ra: : ∠ (A₁) + ∠ (B₂) = 180^o.

Vậy hai góc ngoài cùng phía là ∠ A₁ và ∠ B₂ bù nhau.

Chứng minh tương tự có ∠ B₃ và ∠ A₄ bù nhau.

Bài 19 trang 104: Xem hình bên dưới rồi điền vào chỗ trống trong các câu sau:

a) ∠ (EDC) và ∠ (AEB) là cặp góc…

b) ∠ (BED) và ∠ (CDE) là cặp góc…

c) ∠ (CDE) và ∠ (BAT) là cặp góc…

d) ∠ (TAB) và ∠ (DEB) là cặp góc…

e) ∠ (EAB) và ∠ (MEA) là cặp góc…

g) ∠ Một cặp góc so le trong khác là...

h) ∠ Một cặp góc đồng vị khác là,...

Bài giải: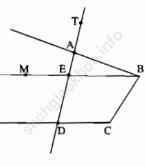

∠ (EDC) và ∠ (AEB) là cặp góc đồng vị

∠ (BED) và ∠ (CDE) là cặp góc trong cùng phía

∠ (CDE) và ∠ (BAT) là cặp góc đồng vị

∠ (TAB) và ∠ (DEB) là cặp góc ngoài cùng phía

∠ (EAB) và ∠ (MEA) là cặp góc so le trong

Một cặp góc so le trong khác là ∠ (MED) và ∠ (EDC)

Một cặp góc đồng vị khác là ∠ (TAB) và ∠ (ADC)

Bài 20 trang 105: Trên hình bên người ta cho biết a // b và ∠ (P₁) =∠ (Q₁) =30^o

a) Viết tên một cặp góc đồng vị khác và nói rõ số đo mỗi góc

b) Viết tên một cặp góc so le trong và nói rõ số đo mỗi góc

c) Viết tên một cặp góc trong cùng phía và nói rõ số đo mỗi góc

d) Viết tên một cặp góc ngoài cùng phía và tổng số đo hai góc đó.

Bài giải:

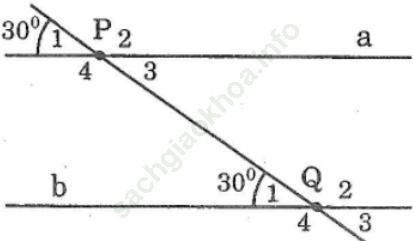
a) Cặp góc đồng vị khác là: ∠ (P₃) = ∠ (Q₃)

Ta có hai góc ∠ (P₃) và ∠ (P₁) là hai góc đối đỉnh nên ∠ (P₃) = ∠ (P₁) = 30º

Lại có: hai góc ∠ (Q₃) và ∠ (Q₁) là hai góc đối đỉnh nên ∠ (Q₃) = ∠ (Q₁) = 30º

Vậy ∠ (P₃) = ∠ (Q₃) = 30º

b) Cặp góc so le trong là: ∠ (P₃) = ∠ (Q₁) = 30º

c) ∠ (P₃) và ∠ (Q₂) là hai góc trong cùng phía.

Trong đó: ∠ (P₃) = 30º

*) Ta tính: ∠ (Q₂):

Hai góc ∠ (Q₂) và ∠ (Q₁) là hai góc kề bù nên: ∠ (Q₂) = 180º - ∠ (Q₁) = 180º – 30º = 150º

d) ∠ (P₁) và ∠ (Q₄) là hai góc ngoài cùng phía

∠ (P₁) = 30º; ∠ (Q₄) = 150º.

*) Ta tính: ∠ (Q₄)

Hai góc ∠ (Q₁) và ∠ (Q₄) là hai góc kề bù nên: ∠ (Q₄) = 180º - ∠ (Q₁) = 180º – 30º = 150º

Bài 3.1 trang 105 sách bài tập Toán 7 Tập 1: Cho hình bs 3 dưới đây. Lần lượt chọn mỗi đường thẳng tk, mz, nj làm cát tuyến, chỉ ra các cặp góc: đồng vị, so le trong, trong cùng phía trong hình đó.

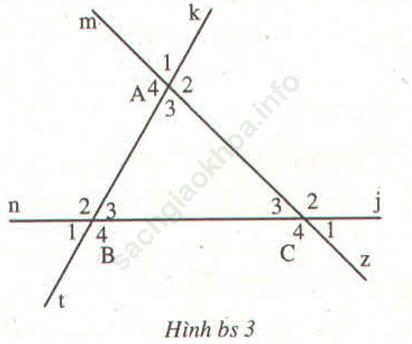
Bài giải:

+) Khi chọn đường thẳng tk làm cát tuyến thì:

Các cặp góc đồng vị là:

Các cặp góc so le trong là:

Các cặp góc trong cùng phía là:

+) Khi chọn đường thẳng nj làm cát tuyến.

+) Khi chọn đường thẳng mz làm cát tuyến.

Bài 3.2 trang 105:

a) Vẽ hình theo diễn đạt sau đây: Hai đường thẳng mn và pq không cho điển chung. Đường thẳng xy cắt đường thẳng mn tại điểm U và cắt đường thẳng pq tại điểm V. Biết rằng: ∠ (V₁) và ∠ (U₁) là hai góc trong cùng phía; ∠ (U₂) và ∠ (V₁) là hai góc đồng vị; ∠ (V₂) và ∠ (U₁) là hai góc so le trong

b) Khi biết thêm ∠ (U₁) = ∠ (V₂) = 36^o, hãy tìm số đo của các góc ∠ V₁ và ∠ (U₂)

Bài giải: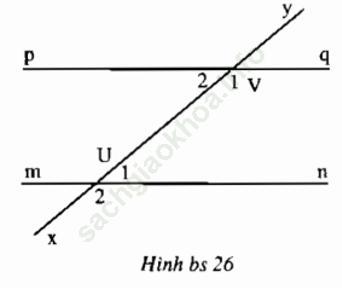

a) Học sinh vẽ được như hình bs 26.

b) ∠ V₂ và ∠ U₁ là hai góc SLT

∠ U₁ và ∠ U₂ kề bù

⇒ ∠ U₁ + ∠ U₂ = 180^o

⇒ ∠ U₂ = 180º - ∠ U₁ = 180º – 36º = 144^o

Theo đề bài ∠ U₁ = ∠ V₂ = 36º mà hai góc này ở vị trí so le trong, do đó theo tính chất cặp góc đồng vị ∠ V₁; ∠ U₂ cũng bằng nhau.

⇒ ∠ V₁ = ∠ U₂ = 144^o.

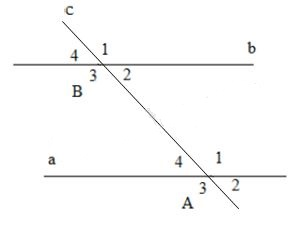
Bài 3.3 trang 105: Một đường thẳng cắt hai đường thẳng khác tạo ra các cặp góc so le trong, các góc trong cùng phía, … Biết rằng trong số đó có một cặp góc so le trong bằng nhau, khi đó mỗi kết quả sau là đúng hay sai?

a) Cặp góc so le trong còn lại bằng nhau.

b) Mỗi cặp góc đồng vị bằng nhau.

c) Mỗi cặp góc trong cùng phía bù nhau.

Bài giải:

Bài trước: Bài 2: Hai đường thẳng vuông góc - trang 102 sách bài tập Toán 7 Tập 1 Bài tiếp: Bài 4: Hai đường thẳng song song - trang 106 sách bài tập Toán 7 Tập 1