Bài 7: Định lí - trang 111 sách bài tập Toán 7 Tập 1
Bài 39 trang 111 sách bài tập Toán 7 Tập 1: Vẽ hình và viết giả thiết, kết luận của các định lý sau:
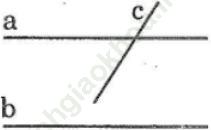
a. Nếu một đường thẳng cắt một trong hai đường thẳng song song thì nó cắt đường thẳng kia
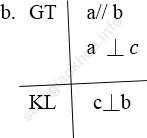
b. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.
Bài giải: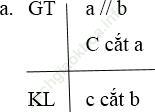
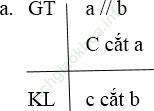
Bài 40 trang 112: Vẽ hình và viết giả thiết, kết luận của các định lý sau:
a. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau
b. Hai đường thẳng song song với một đường thẳng thứ ba thì chúng song song với nhau
Bài giải: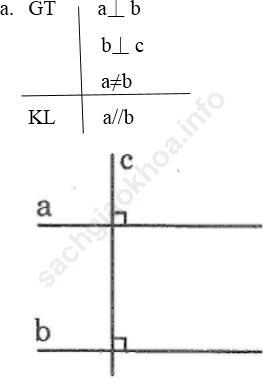
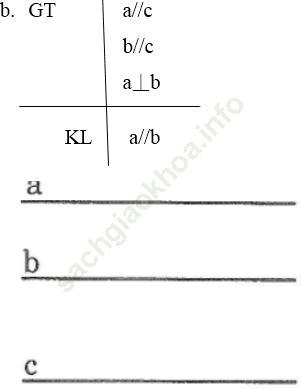
Bài 41 trang 112: Với hai góc kề bù ta có định lý sau:
Hai tia phân giác của hai góc kề bù tạo thành một góc vuông
a. Hãy vẽ hai góc xOy và yOx’ kề bù, tia phân giác Ot của góc xOy, tia phân giác Ot’ của góc yOx’ và gọi số đo của góc xOy là mº.
b. Hãy viết giả thiết và kết luận của định lí
c. Hãy điền vào chỗ trống và sắp xếp bốn câu sau đây một cách hợp lí để chứng minh định lí trên.
∠ (tOy) = (1/2). mo vì…
∠ (t'Oy) = (1/2)(180o - mo)vì…
∠ (tOt') = 90o vì…
∠ (x'Oy) = (180o - mo) vì…
Bài giải:a. Hình vẽ:
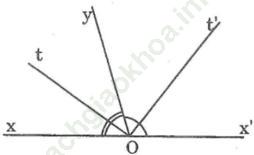
b.

c. Chứng minh:
1) ∠ tOy = 1/2. ∠ xOy = 1/2. mo (Vì Ot là tia phân giác của góc xOy)
4) ∠ x'Oy = 180o - ∠ xOy = 180o - mo (Vì ∠ x'Oy và ∠ xOy kề bù)
2) ⇒ ∠ t'Oy = 1/2. ∠ x'Oy = 1/2. (180o - mo) (Vì Ot’ là phân giác của ∠ x'Oy)
3) ⇒ ∠ tOt' = ∠ tOy + ∠ t'Oy = 1/2. mo + 1/2. (180o - mo) = 90o.
Kết luận: Vậy hai tia phân giác của hai góc kề bù tạo thành góc vuông.
Bài 42 trang 112: Điền vào chỗ trống để chứng minh bài toán sau:
Gọi DI là tia phân giác của góc MDN. Gọi EDK là góc đối đỉnh của góc IDM. Chứng minh rằng
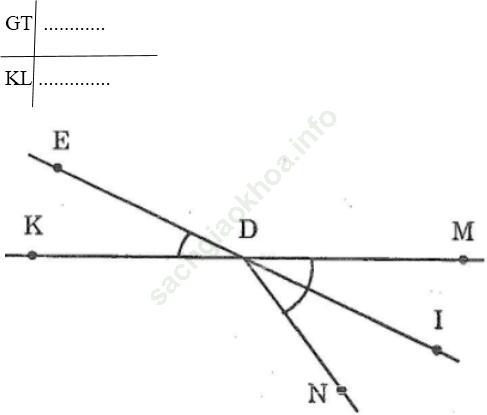
Chừng minh:
∠ (IDM) =∠ (IDN) (vì…) (1)
∠ (IDM) =∠ (EDK) (vì…) (2)
Từ (1) và (2) suy ra...
Đó là điều phải chứng minh

Chứng minh:
∠ (IDM) =∠ (IDN) (vì DI là tia phân giác của ∠ (MDN) (1)
∠ (IDM) =∠ (EDK) (vì 2 góc đối đỉnh) (2)
Từ (1) và (2) suy ra ∠ (EDK) =∠ (IDN) (điều phải chứng minh)
Bài 43 trang 112: Hãy chứng minh định lí:
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Hướng dẫn: chứng minh tương tự bài tập 30.
Bài giải: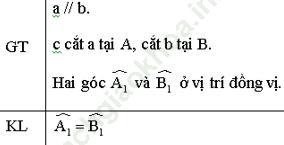
Chứng minh
Giả sử ∠ (A1) ≠ ∠ (B1)
Qua B kẻ đường thẳng xy sao cho ∠ (ABy) = ∠ (A1)
Mà hai góc này ở vị trí so le trong nên theo dấu hiệu của hai đường thẳng song song, ta có xy //a
+) Qua điểm B ta kẻ được hai đường thẳng b và xy cùng song song với đường thẳng a. Theo tiên đề Ơ- clit suy ra đường thẳng xy trùng với đường thẳng b.
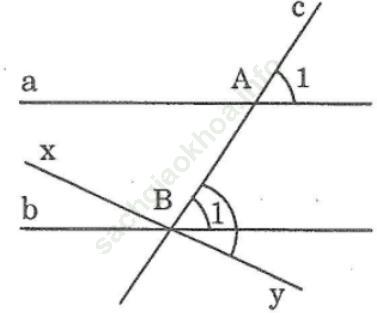
Bài 44 trang 113: Chứng minh rằng:
Nếu hai góc nhọn xOy và x’Oy’ có Ox// O’x’; Oy//O’y’ thì ∠ (xOy) = ∠ (x'O'y')
Hướng dẫn: sử dụng tính chất của hai đường thẳng song song (bài 5)
Bài giải: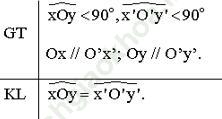
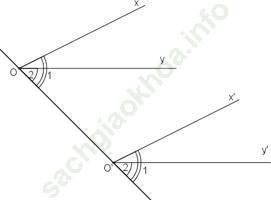
Chứng minh:
Vẽ đường thẳng OO’
Vì Ox // O’x’ nên hai góc đồng vị ∠ (O1) và ∠ (O'1) bằng nhau
Suy ra: ∠ (O1) = ∠ (O'1) (1)
Vì Oy // O’y’ nên hai góc đồng vị ∠ (O2) và ∠ (O'2) bằng nhau
Suy ra: ∠ (O2) = ∠ (O'2) (2)
Từ (1) và (2) suy ra: ∠ (O1) - ∠ (O2) =∠ (O'1) - ∠ (O'2)
Vậy ∠ (xOy) = ∠ (x'O'y')
Bài 7.1 trang 113 sách bài tập Toán 7 Tập 1: Ghi giả thiết, kết luận và chứng minh định lý: “ Hai góc cùng phụ với một góc thứ ba thì bằng nhau ”.
Bài giải:
Chứng minh:
∠ B phụ với ∠ A ⇒ ∠ B + ∠ A = 90o ⇒ ∠ B = 90o - ∠ A
∠ C phụ với ∠ A ⇒ ∠ C + ∠ A = 90o ⇒ ∠ C = 90o - ∠ A
Vậy ∠ B = ∠ C.
Bài 7.2 trang 113: Ghi giả thiết, kết luận và chứng minh định lý: “ Hai góc cùng bù với một góc thứ ba thì bằng nhau”.
Bài giải: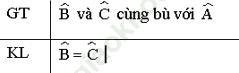
Chứng minh:
∠ B bù với ∠ A ⇒ ∠ B + ∠ A = 180o ⇒ ∠ B = 180o - ∠ A
∠ C bù với ∠ A ⇒ ∠ C + ∠ A = 180o ⇒ ∠ C = 180o - ∠ A
Vậy ∠ B = ∠ C.
Bài 7.3 trang 113: Ghi giả thiết, kết luận và chứng minh định lý: “Nếu hai đường thẳng a, b cắt đường thẳng c và trong các góc tạo thành có một cặp trong cùng phía bù nhau thì a và b song song với nhau”.
Bài giải:
Chứng minh: