Bài 9: Độ dài đường tròn, cung tròn - trang 109 Sách bài tập Toán 9 Tập 2
Bài 9: Độ dài đường tròn, cung tròn
Bài 52 trang 109 Sách bài tập Toán 9 Tập 2: Cho hai đường tròn bán kính lần lượt R = 1km và r = 1m. Nếu độ dài mỗi đường tròn ấy đều tăng thêm 1m thì bán kính của mỗi đường tròn tăng thêm bao nhiêu? Hãy giải thích
Bài giải:Gọi a và b lần lươt là phần bán kính tăng thêm của đường tròn bán kính R và đường tròn bán kính r.
Khi bán kính của mõi đường tròn tăng thêm 1m ta có:

Bài 53 trang 109 Sách bài tập Toán 9 Tập 2: Tính độ dài đường tròn ngoại tiếp
a. Một lục giác đều có cạnh là 4cm
b. Một hình vuông có cạnh là 4cm
c. Một tam giác đều có cạnh là 6cm
Bài giải:a. Đường tròn ngoại tiếp một lục giác đều có cạnh là 4cm
Cạnh lục giác đều nội tiếp trong đường tròn (O; R) bằng bán kính R.
Vì lục giác đều có cạnh bằng 4cm nên R =4cm
Độ dài đường tròn là: C = 2πR=2π4=8π (cm)
c. Đường tròn ngoại tiếp hình vuông có cạnh là 4cm
Vì hình vuông có cạnh bằng 4cm nên đường chéo sẽ là: 4√ 2 cm
Bán kính của đường tròn ngoại tiếp hình vuông là:
Độ dài đường tròn là:
C = 2π R= 2π 2√ 2 =4√ 2π cm
c. Đường tròn ngoại tiếp tam giác đều có cạnh là 6cm
Trong tam giác đều, giao điểm ba đường trung trực cũng là giao điểm của ba đường cao, ba đường trung tuyến. Do vậy bán kính của đường tròn ngoại tiếp bằng 2/3 đường cao của tam giác đều
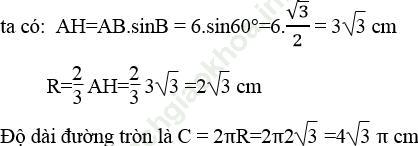
Bài 54 trang 110 Sách bài tập Toán 9 Tập 2: Xích đạo là một đường tròn lớn của Trái Đất có độ dài khoảng 40000km. Hãy tính bán kính của Trái Đất
Bài giải:Gọi R là bán kính của Trái Đất:
Ta có: 2π R = 40000 (km) ⇒ R = 40000/2.3,14 ≈ 6369 (km)
Bài 55 trang 110 Sách bài tập Toán 9 Tập 2: Mát-cơ-va có vĩ độ 56° bắc. Tính độ dài cung kinh tuyến từ mát-cơ-va đến xích đạo, biết rằng mỗi kinh tuyến là một nửa đường tròn lớn của trái đât có độ dài khỏang 20000km
Bài giải:Một nửa đường tròn lớn của trái đât có độ dài bằng 20000km
Suy ra độ dài của cung 56° là:
l= (20000.56)/180 = 6222 (km)
Vậy mát-cơ-va cách xích đạo gần 6222km
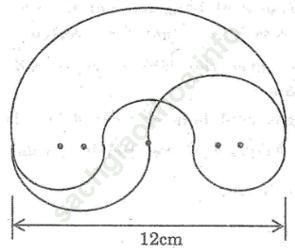
Bài 56 trang 110 Sách bài tập Toán 9 Tập 2: Hãy so sánh độ dài ba đường cong a, b, c trong hình sau:
Bài giải:
Đường cong a là nửa đường tròn đường kính 12cm nên có độ dài là:
Đường cong b gồm ba nửa đường tròn đường kính 4cm nên có độ dài là:
Đường cong c gồm hai nửa đường tròn đường kính 6cm nên có độ dài là:
Vậy ba đường cong có độ dài bằng nhau
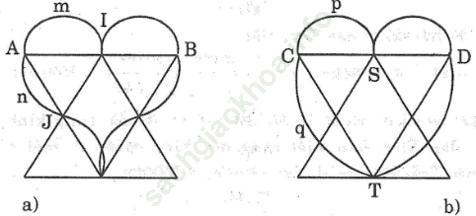
Bài 57 trang 110 Sách bài tập Toán 9 Tập 2: Các tam giác trong hai hình quả tim dưới đây đều là tam giác đều. Biết AB=CD=8cm. Tính chu vi của mỗi hình quả tim
Bài giải:
* Hình a có hai nửa đường tròn đường kính 4cm

* Hình b gồm hai nửa đường tròn đường kính 4cm và hai cung 1/6 đường tròn đường kính 8cm

Bài 58 trang 110 Sách bài tập Toán 9 Tập 2: Vẽ hình quả trứng với AB =3cm. Nêu cách vẽ. Tính chu vi của hình quả trứng đó?
Bài giải: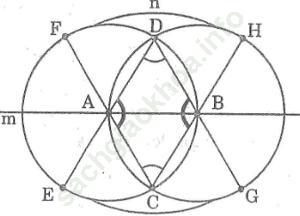
* Cách vẽ:
- Vẽ đoạn thẳng AB=3cm
- Vẽ đường tròn tâm A bán kính 3cm
- Vẽ đường tròn tâm B bán kính 3cm
Đường tròn (A) và đường tròn (B) cắt nhau tại C và D
- Vẽ cung tròn tâm C bán kính 6cm cắt đường tròn (A) và (B) tại F và H
- Vẽ cung tròn tâm D bám kính 6cm cắt đường tròn (A) và (B) tại E và G
* Tính chu vi:
Ta có: Δ ABD đều, Δ ACD đều

Chu vi hình quả trứng bằng: 2. l1 + 2. l2 = 2.2π + 2.2π =8π (cm)
Bài 59 trang 110 Sách bài tập Toán 9 Tập 2: Tính độ dài cung 36o45’ của một đường tròn có bán kính là R.
Bài giải: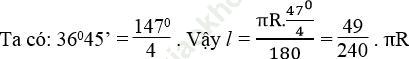
Bài 60 trang 110 Sách bài tập Toán 9 Tập 2: Cho tam giác cân ABC có góc B = 120°, AC = 6cm. Tính độ dài đường tròn ngoại tiếp tam giác đó?
Bài giải: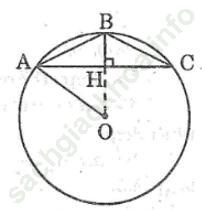

Bài 61 trang 110 Sách bài tập Toán 9 Tập 2: Trong dân gian Việt Nam có lưu truyền quy tắc sau đây để tìm đường kính khi biết độ dài đường tròn: “Quân bát, phát tam, tồn ngũ, quân nhị”, tức là chia đường tròn thành 8 phần, bỏ đi 3 phần, còn lại 5 phần, lại chia đôi.
a. Theo quy tắc đó thì π được lấy đúng là bao nhiêu?
b. Hãy áp dụng quy tắc trên để tính đường kính của một thân cây gần tròn bằng cách dùng dây quấn quanh thân cây.
Bài giải:a. Gọi C là độ dài đường tròn, d là đường kính đường tròn.
Ta có: π = C/d
Theo quy tắc trên thì ta tìm được đường kính d như sau: Lấy C chia làm 8 phần, bỏ đi 3 phần, còn lại chia 2.
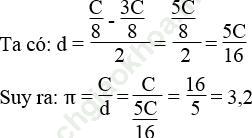
Vậy theo quy tắc trên thì π được lấy gần đúng 3,2.
b. Lấy dây quấn quanh thân cây sẽ biết được chu vi thân cây là C. Suy ra đường kính thân cây là 5C/16.
Bài 62 trang 110 Sách bài tập Toán 9 Tập 2: Trái Đất quay xung quanh Mặt Trời theo một quỹ đạo gần tròn. Giả thiết quỹ đạo này tròn và có bán kính khoảng 150 triệu kilomet. Cứ hết một năm thì Trái Đất quay được một vòng quanh Mặt Trời. Biết một năm có 365 ngày, hãy tính quãng đường đi được của Trái Đất sau một ngày (làm tròn đến 10000km)
Bài giải:Quãng đường đi của Trái Đất trong một ngày là:
[2. (3,14).150000000]/365 ≈ 2580822 ≈ 2580000 (km)
Bài 1 trang 111 Sách bài tập Toán 9 Tập 2: Tính chu vi của hình bên biết OA = OB = R > 0 (h. bs. 5).
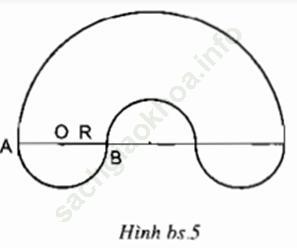
Bài giải:
Hình đó gồm một nửa đường tròn bán kính 3R và 3 nửa đường tròn có bán kính R. Do đó, chu vi của hình đã cho là
Bài 2 trang 111 Sách bài tập Toán 9 Tập 2: Tính chu vi của hình cánh hoa, biết OA = R (h. bs. 6).
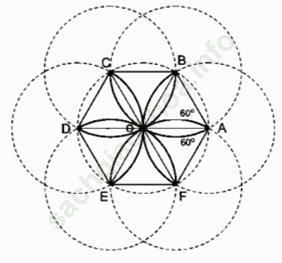
Bài giải:
Ta có 12 cung đơn hoặc 6 cung kép tạo nên cánh hoa đó.
Xét một cung kép, chẳng hạn BOF, là cung của một đường tròn tâm A bán kính R với góc ở tâm là 120o, nên có độ dài là
