Bài 2: Tỉ số lượng giác của góc nhọn - trang 106 Sách bài tập Toán 9 Tập 1
Bài 2: Tỉ số lượng giác của góc nhọn
Bài 21 trang 106 Sách bài tập Toán 9 Tập 1: Vẽ một tam giác vuông có một góc nhọn bằng 40o rồi viết các tỉ số lượng giác của góc 40o
Bài giải:

Bài 22 trang 106 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A. Chứng minh rằng
Bài giải:
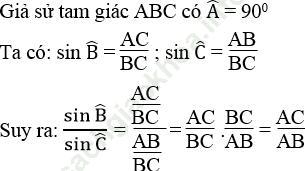
Bài 23 trang 106 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, góc B = 30o, BC = 8cm. Hãy tính cạnh AB (làm tròn đến chữ số thập phân thứ ba), biết rằng cos30o ≈ 0,866
Bài giải: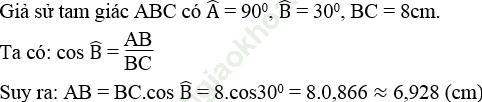
Bài 24 trang 106 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, AB = 6cm, góc B = α
Biết tg α = 5/12. Hãy tính:
a. Cạnh AC b. Cạnh BC
Bài giải:
Bài 25 trang 107 Sách bài tập Toán 9 Tập 1: Tìm giá trị của x (làm tròn đến chữ số thập phân thứ ba) trong mỗi tam giác vuông với kích thước được chỉ ra trên hình sau, biết:
tg47o ≈ 1,072, cos38o ≈ 0,788
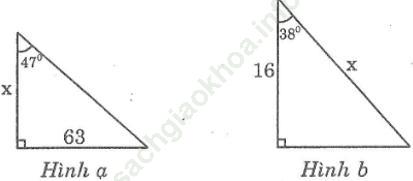
Bài giải:
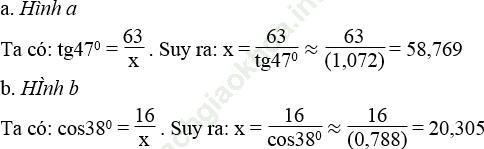
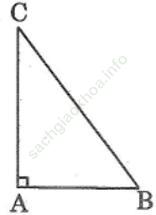
Bài 26 trang 107 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.
Bài giải:
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100
Suy ra: BC = 10 (cm)
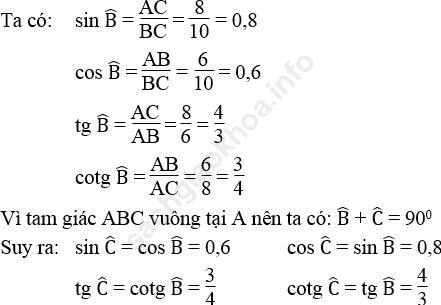
Bài 27 trang 107 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC trong mỗi trường hợp sau (làm tròn đến chữ số thập phân thứ tư), biết rằng:
a. AB = 13, BH = 5 b. BH = 3, CH = 4
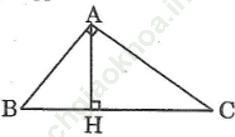
Bài giải:

Bài 28 trang 107 Sách bài tập Toán 9 Tập 1: Hãy biến đổi các tỉ số lượng giác sau đây thành tỉ số lượng giác của các góc nhỏ hơn 45o: sin75o, cos53o, sin47o20’, tg62o, cotg82o45’
Bài giải:Vì 75o + 15o = 90o nên sin75o = cos15o
Vì 53o + 37o = 90o nên cos53o = sin37o
Vì 47o20’ + 42o40’ = 90o nên sin47o20’ = cos42o40’
Vì 62o + 28o = 90o nên tg62o = cotg28o
Vì 82o45’ + 7o15’ = 90o nên cotg82o45’ = tg7o15’
Bài 29 trang 107 Sách bài tập Toán 9 Tập 1: Xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính:
a. ![]()
b. tg76o – cotg14o
Bài giải:a. Ta có: 32o + 58o = 90o
Suy ra: sin32o = cos58o. Vậy
b. Ta có: 76o + 14o = 90o
Suy ra: tg76o= cotg14o. Vậy tg76o – cotg14o = 0
Bài 30 trang 107 Sách bài tập Toán 9 Tập 1: Đường cao MQ của tam giác vuông MNP chia cạnh huyển NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotg ![]() và cotg
và cotg ![]() . Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
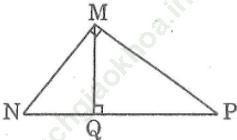
Bài giải:

Bài 31 trang 108 Sách bài tập Toán 9 Tập 1: Cạnh góc vuông kề với góc 60o của một tam giác vuông bằng 3. Sử dụng bảng lượng giác của các góc đặc biệt, hãy tìm cạnh huyền và cạnh góc vuông còn lại (làm tròn đến chữ số thập phân thứ tư)
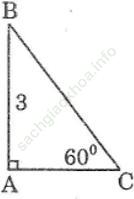
Bài giải:

Bài 32 trang 108 Sách bài tập Toán 9 Tập 1: Đường cao BD của tam giác nhọn ABC bằng 6, đoạn thẳng AD bằng 5.
a. Tính diện tích tam giác ABD
b. Tính AC, dùng các thông tin dưới đây nếu cần:
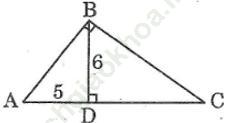
Bài giải:

Suy ra: AC = AD + DC = 5 + 8 = 13.
Bài 33 trang 108 Sách bài tập Toán 9 Tập 1: Cho cos α = 0,8. Hãy tìm sin α, tg α, cotg α (làm tròn đến chữ số thập phân thứ tư)
Bài giải:Ta có: sin2α + cos2α = 1
Suy ra: sin2α = 1 – cos2α = 1 – (0,8)2 = 1 – 0,64 = 0,36
Vì sin α > 0 nên sin α = √ 0,36 = 0,6
Suy ra: tg α = sinα /cosα = 0,6/0,8 = 3/4 = 0,75
cotg α = 1/tgα = 1/0,75 = 1,3333
Bài 34 trang 108 Sách bài tập Toán 9 Tập 1: Hãy tìm sin α, cos α (làm tròn đến chữ số thập phân thứ tư) nếu biết:
a. tg α = 1/3 b. cotg α = 3/4
Bài giải:a. Vì tg α = 1/3 nên α là góc nhọn của một tam giác vuông có các cạnh góc vuông là 1 và 3.
Suy ra cạnh huyền của tam giác vuông là:
Vậy: sin α = 3/5 ≈ 0,6 cos α = 4/5 ≈ 0,8
Bài 35 trang 108 Sách bài tập Toán 9 Tập 1: Dựng góc nhọn α, biết rằng:
a. sin α = 0,25 b. cos α = 0,75
c. tg α = 1 d. cotg α = 2
Bài giải:a. sin α = 0,25 = 14
*Cách dựng: hình a
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 1 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
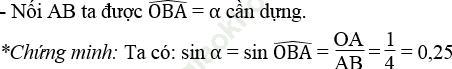
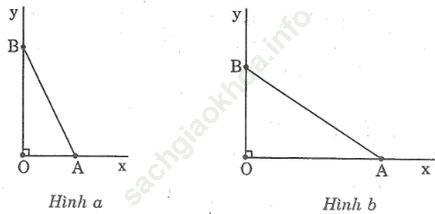
b. cos α = 0,75
*Cách dựng: hình b
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 3 đơn vị dài
- Dựng cung tròn tâm A bán kính 4 đơn vị dài và cắt Oy tại B
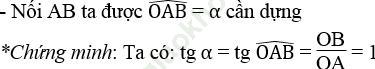
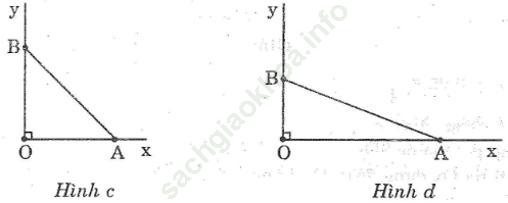
d. cotg α = 2
*Cách dựng: hình d
- Dựng góc vuông xOy
- Trên tia Ox dựng đoạn OA bằng 2 đơn vị dài
- Trên tia Oy dựng đoạn OB bằng 1 đơn vị dài
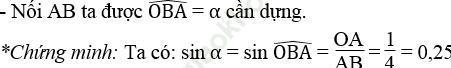
Bài 36 trang 108 Sách bài tập Toán 9 Tập 1: Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau: A (1; 1), B (5; 1), C (7; 9)
Hãy tính:
a. Giá trị của tg ![]() (làm tròn đến chữ số thập phân thứ tư)
(làm tròn đến chữ số thập phân thứ tư)
b. Độ dài của cạnh AC
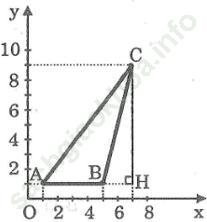
Bài giải:

Bài 37 trang 108 Sách bài tập Toán 9 Tập 1: Cho hình dưới. Hãy viết một phương trình để từ đó có thể tìm được x (không phải giải phương trình này).
Bài giải: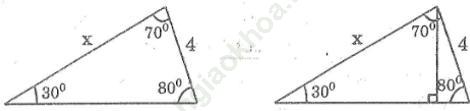
Từ đỉnh của góc 70o, kẻ đường cao của tam giác.
Sử dụng tỉ số sin của các góc, ta có phương trình: xsin30o = 4sin80o
Bài 38 trang 108 Sách bài tập Toán 9 Tập 1: Cho hình bên dưới. Hãy tính sin ![]() (làm tròn đến chữ số thập phân thứ tư), biết rằng sin30o = 0,5.
(làm tròn đến chữ số thập phân thứ tư), biết rằng sin30o = 0,5.
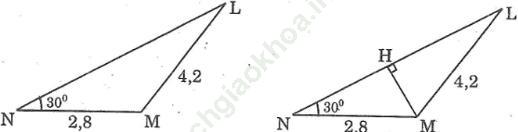
Kẻ MH ⊥ NL
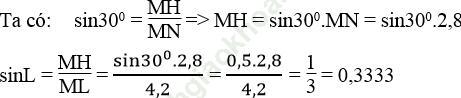
Bài 1 trang 109 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng
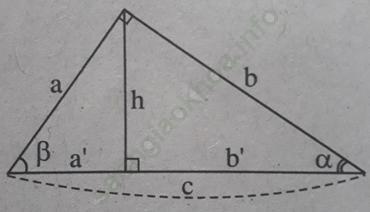
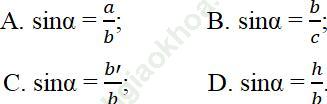
Bài giải:
Chọn đáp án D
Bài 2 trang 109 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng
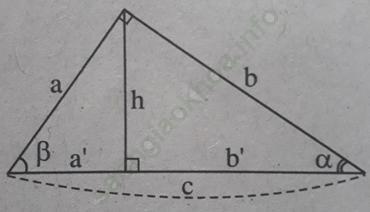

Bài giải:
Chọn đáp án C
Bài 3 trang 109 Sách bài tập Toán 9 Tập 1:
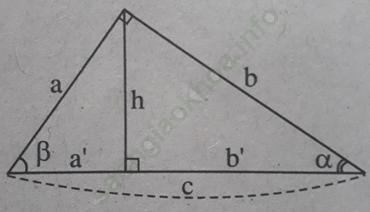

Bài giải:
Chọn đáp án D
Bài 4 trang 109 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng
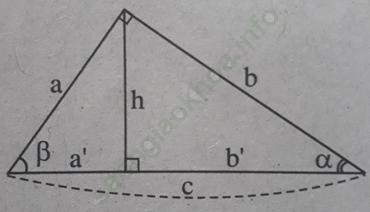
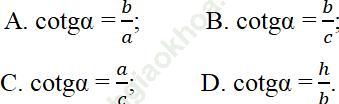
Bài giải:
Chọn đáp án A
Bài 5 trang 109 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng
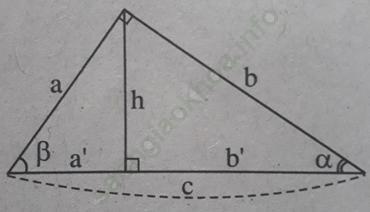
A. sinα = sinβ; B. sinα = cosβ;
C. sinα = tgβ; D. sinα = cotgβ.
Bài giải:Chọn đáp án B
Bài 6 trang 109 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng
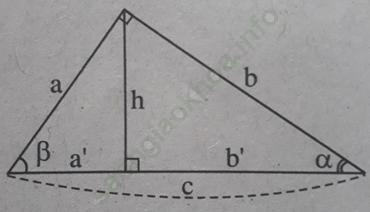
A. cosα = cosβ; B. cosα = tgβ;
C. cosα = cotgβ; D. cosα = sinβ.
Bài giải:Chọn đáp án D
Bài 7 trang 109 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng

A. tgα = tgβ; B. tgα = cotgβ;
C. tgα = sinβ; D. tgα = cosβ.
Bài giải:Chọn đáp án B
Bài 8 trang 109 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng
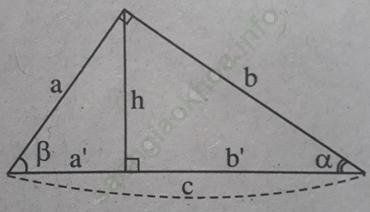
A. cotgα = tgβ; B. cotgα = cotgβ;
C. cotgα = cosβ; D. cotgα = sinβ;
Bài giải:Chọn đáp án A
Bài 9 trang 109 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng
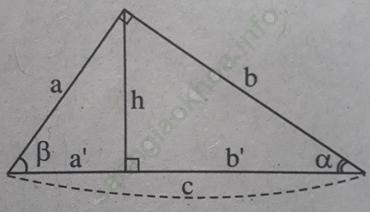
A. cos2 α + sin2 β = 1; B. sin2 α + cos2 β = 1;
C. cos2 α + sin2 α = 1; D. cos2 α + sin2 β = 2.
Bài giải:Chọn đáp án C
Bài 10 trang 109 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng
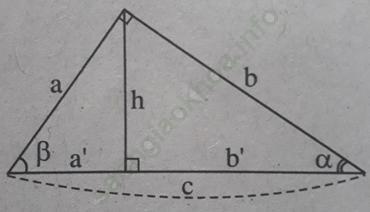
A. tgα = sinα + cosα; B. tgα = sinα - cosα;
C. tgα = sinα. cosα; D. tgα = sinα /cosα.
Bài giải:Chọn đáp án D
Bài 11 trang 110 Sách bài tập Toán 9 Tập 1: Tìm đẳng thức đúng
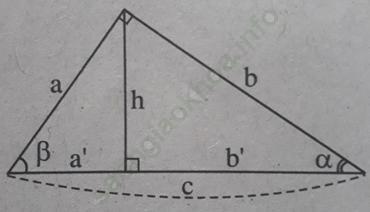
A. cotgα = 1 + tgα; B. cotgα = 1 - tgα;
C. cotgα = 1. tgα; D. cotgα = 1/tgα.
Bài giải:Chọn đáp án D
Bài 12 trang 110 Sách bài tập Toán 9 Tập 1: Cho sinα = 1/2. Hãy tìm cosα, tgα, cotgα (0o < α < 90o).
Bài giải:
Bài 13 trang 110 Sách bài tập Toán 9 Tập 1: Cho cosα = 3/4. Hãy tìm sinα, tgα, cotgα (0o < α < 90o).
Bài giải: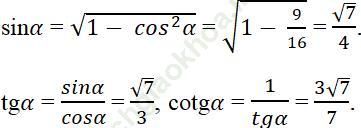
Bài 14 trang 110 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, có AB = 1/3BC. Hãy tính sinC, cosC, tgC, cotgC.
Bài giải: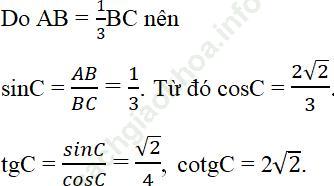
Bài 15 trang 110 Sách bài tập Toán 9 Tập 1: Hãy tính
a) 2sin30o - 2cos60o + tg45o;
b) sin45o + cotg60o.cos30o;
c) cotg44o.cotg45o.cotg46o.
Bài giải:a) 2sin30o - 2cos60o + tg45o = tg45o = 1 (do sin30o = cos60o).
b) sin45o + cotg60o.cos30o = (1+ √ 2)/2.
c) cotg44o.cotg45o.cotg46o = cotg45o = 1
(vì cotg44o = tg46o do 44o + 46o = 90o mà tg46o.cotg46o = 1)
Bài 16 trang 110 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC có ∠ A = 60o. Chứng minh rằng: BC2 = AB2 + AC2 – AB. AC.
Bài giải: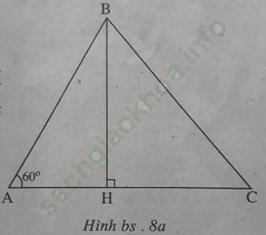
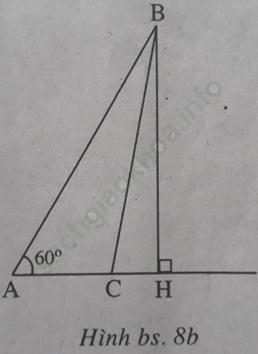
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠ (BAC) = 60o là góc nhọn), do đó HC2 = (AC-AH)2(xem h. bs. 8a, 8b)
Công thức Py-ta-go cho ta
BC2 = BH2 + HC2
= BH2 + (AC-AH)2
= BH2 + AC2 + AH2 – 2AC. AH
= AB2 + AC2 – 2AC. AH.
Do ∠ (BAC) = 60o nên AH = AB. cos60o = AB/2, suy ra BC2 = AB2 + AC2 – AB. AC
Bài 17 trang 110 Sách bài tập Toán 9 Tập 1: Cho tứ giác ABCD có α là góc nhọn tạo bởi hai đường chéo chứng minh rằng SABCD = 1/2 AC. BD. sinα.
Bài giải: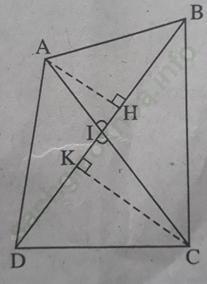
Giả sử hai đường chéo AC, BD cắt nhau tại I, (AIB) ̂ = α là góc nhọn (xem h. bs. 9)
Kẻ đường cao AH của tam giác ABD và đường cao CK của tam giác CBD.
Ta có: AH = AI. sinα, CK = CI. sinα,
Diện tích tam giác ABD là SABD = 1/2 BD. AH.
Diện tích tam giác CBD là SCBD = 1/2 BD. CK.
Từ đó diện tích S của tứ giác ABCD là:
S = SABD + SCBD = 1/2BD. (AH + CK)
= 1/2 BD. (AI + CI)sinα = 1/2BD. AC. sinα
Bài 18 trang 110 Sách bài tập Toán 9 Tập 1: Cho góc nhọn α

Bài giải:
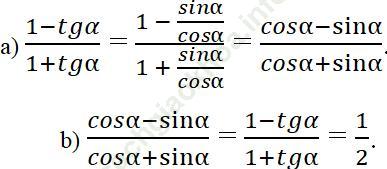
Bài 19 trang 110 Sách bài tập Toán 9 Tập 1: Tính giá trị của biểu thức

Bài giải:
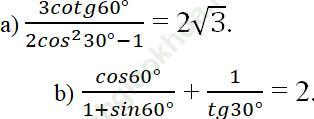
Bài 20 trang 110 Sách bài tập Toán 9 Tập 1: Trong hình thang vuông ABCD với các đáy AD, BC có ∠ A = ∠ B = 90o, ∠ (ACD) = 90o. BC = 4cm, AD = 16cm. Hãy tìm các góc C và D của hình thang.
Bài giải: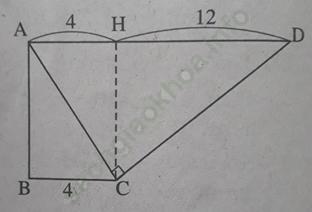
Kẻ đường cao CH của tam giác ACD vuông tại C. Khi đó
AH = BC = 4, HD = AD – AH = 12.
Từ đó
HC2 = HA. HD = 48, vậy HC = 4√ 3.
Trong tam giác vuông HCD, ta có
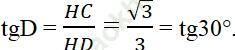
Nên ∠ D = 30o. Suy ra ∠ (BCD) = 180o - 30o = 150o.
Bài 21 trang 111 Sách bài tập Toán 9 Tập 1: Tính các góc của một hình thoi, biết hai đường chéo của nó có độ dài là 2√ 3 và 2.
Bài giải: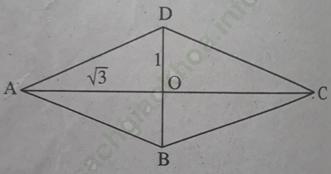
Coi đường chéo AC = 2√ 3, đường chéo BD = 2 thì để ý rằng AC và BD vuông góc, ta có
Nên ∠ (DAC) = 30o từ đó góc A của hình thoi là 60o. Suy ra ∠ C = 60o còn ∠ B = ∠ D = 120o.
Bài 22 trang 111 Sách bài tập Toán 9 Tập 1: Các cạnh của một hình chữ nhật bằng 3cm và √ 3 cm. Hãy tìm các góc hợp bởi đường chéo và các cạnh của hình chữ nhật đó.
Bài giải: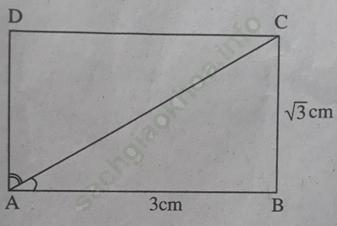
Hình chữ nhật ABCD có AB = 3cm, BC = √ 3 cm nên
Vậy ∠ (BAC) = 30o.
∠ (DAC) = 90o - 30o = 60o.