Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số - trang 11 Sách bài tập Toán 9 Tập 2
Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
Bài 25 trang 11 Sách bài tập Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:
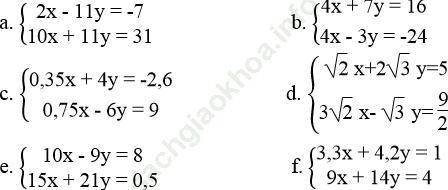
Bài giải:
Bài 26 trang 11 Sách bài tập Toán 9 Tập 2: Giải các hệ phương trình:
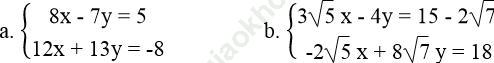
Bài giải:
Bài 27 trang 11 Sách bài tập Toán 9 Tập 2: Giải các hệ phương trình:
Bài giải:
Vì phương trình 0x – 0y = 39 vô nghiệm nên hệ phương trình đã cho vô nghiệm.
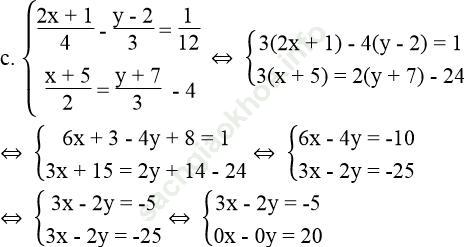
Vì phương trình 0x – 0y = 20 vô nghiệm nên hệ phương trình đã cho vô nghiệm.
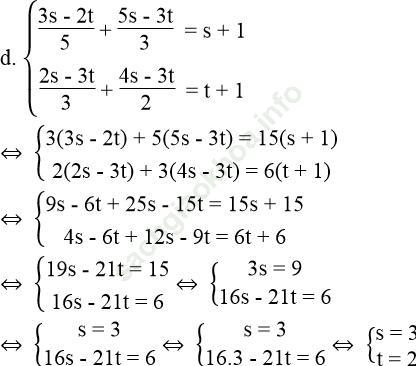
Vậy hệ phương trình đã cho có nghiệm (s; t) = (3; 2)
Bài 28 trang 11 Sách bài tập Toán 9 Tập 2: Tìm hai số a và b sao cho 5a – 4b = -5 và đường thẳng: ax + by = -1 đi qua điểm A (-7; 4).
Bài giải:Đường thẳng ax + by = -1 đi qua điểm A (-7; 4) nên tọa độ của A nghiệm đúng phương trình đường thẳng.
Khi đó ta có phương trình:
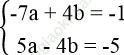
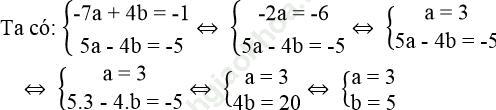
Vậy a = 3, b = 5.
Bài 29 trang 11 Sách bài tập Toán 9 Tập 2: Tìm giá trị của a và b để đường thẳng ax – by = 4 đi qua hai điểm A (4; 3), B (-6; -7)
Bài giải:Đường thẳng ax – by = 4 đi qua hai điểm A (4; 3), B (-6; -7) nên tọa độ của A và B nghiệm đúng phương trình đường thẳng.
* Với điểm A: 4a – 3b = 4
* Với điểm B: -6a + 7b = 4
Hai số a và b là nghiệm của hệ phương trình:
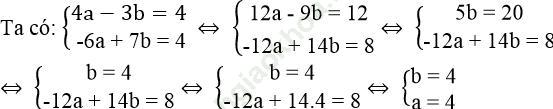
Vậy a = 4, b = 4.
Bài 30 trang 11 Sách bài tập Toán 9 Tập 2: Giải các hệ phương trình theo hai cách:
* Cách 1: Đưa hệ phương trình về dạng:
* Cách 2: Đặt ẩn phụ, chẳng hạn s = 3x – 2, t = 3y + 2
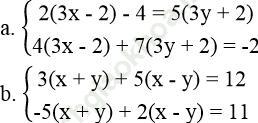
Bài giải:
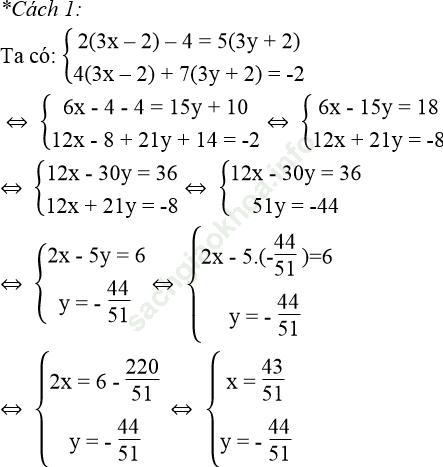
Vậy hệ phương trình đã cho có nghiệm (x; y) = (43/51; -44/51)
* Cách 2: Đặt m = 3x – 2, n = 3y + 2
Ta có hệ phương trình:
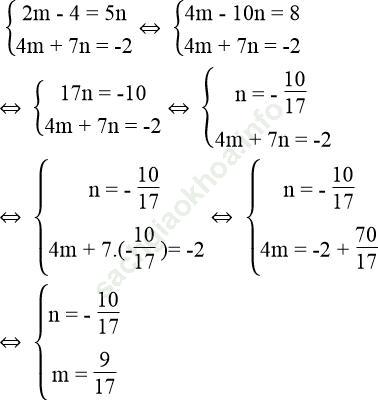
Ta có: 3x – 2 = 9/17 ⇔ 3x = 2 + 9/17 ⇔ 3x = 43/17 ⇔ x = 43/51
3y + 2 = - 10/17 ⇔ 3y = -2 - 10/17 ⇔ 3y = - 44/17 ⇔ y = - 44/51
Vậy hệ phương trình đã cho có nghiệm (x; y) = (43/51; -44/51)
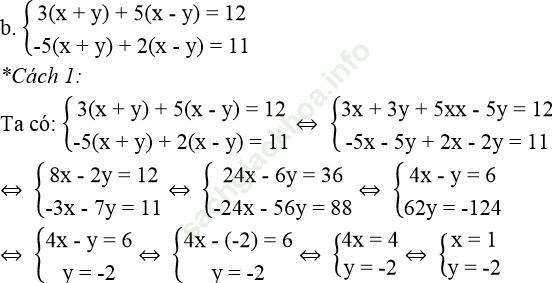
Vậy hệ phương trình có nghiệm (x; y) = (1; -2)
* Cách 2: Đặt m = x + y, n = x – y
Ta có hệ phương trình:
Vậy hệ phương trình có nghiệm (x; y) = (1; -2)
Bài 31 trang 12 Sách bài tập Toán 9 Tập 2: Tìm giá trị của m để nghiệm của hệ phương trình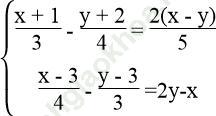 
cũng là nghiệm của phương trình 3mx – 5y = 2m + 1.
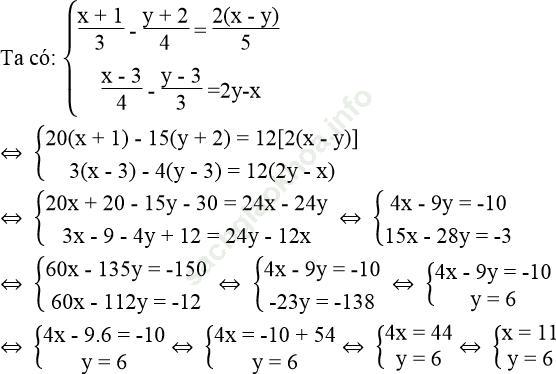
Vì (x; y) = (11; 6) là nghiệm của phương trình 3mx – 5y = 2m +1 nên ta có:
3m. 11 – 5.6 = 2m + 1
⇔ 33m – 30 = 2m + 1 ⇔ 31m = 31 ⇔ m = 1
Vậy với m = 1 thì nghiệm của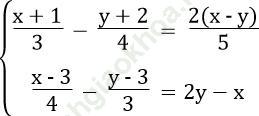 
cũng là nghiệm của phương trình 3mx – 5y = 2m + 1.
Bài 32 trang 12 Sách bài tập Toán 9 Tập 2: Tìm giá trị của m để đường thẳng (d): y = (2m – 5)x – 5m đi qua giao điểm của hai đường thẳng (d1): 2x + 3y = 7 và (d2): 3x + 2y = 13
Bài giải:Gọi I là giao điểm của (d1) và (d2). Khi đó tọa độ của I là nghiệm của hệ phương trình:
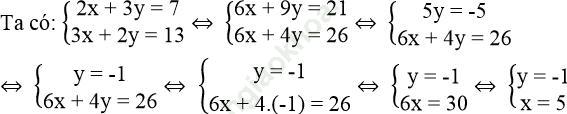
Tọa độ điểm I là I (5; -1)
Đường thẳng (d): y = (2m – 5)x – 5m đi qua I (5; -1) nên tọa độ của I nghiệm đúng phương trình đường thẳng:
Ta có: -1 = (2m – 5).5 – 5m ⇔ -1 = 10m – 25 – 5m
⇔ 5m = 24 ⇔ m = 24/5
Vậy với m = 24/5 thì đường thẳng (d) đi qua giao điểm của hai đường thẳng (d1) và (d2).
Bài 33 trang 12 Sách bài tập Toán 9 Tập 2: Tìm giá trị của m để ba đường thẳng sau đây đồng quy: (d1): 5x + 11y = 8, (d2): 10 – 7y = 74, (d3): 4mx + (2m – 1)y = m + 2
Bài giải:Tọa độ giao điểm của (d1) và (d2) là nghiệm của hệ phương trình:
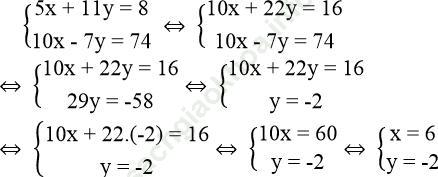
Tọa độ giao điểm của (d1) và (d2) là (x; y) = (6; -2)
Để ba đường thẳng (d1), (d2), (d3) đồng quy thì (d3) phải đi qua giao điểm của (d1) và (d2), nghĩa là (x; y) = (6; -2) nghiệm đúng phương trình đường thẳng (d3).
Khi đó ta có: 4m. 6 + (2m – 1). (-2) = m + 2
⇔ 24m – 4m + 2 = m + 2 ⇔ 19m = 0 ⇔ m = 0
Vậy với m = 0 thì 3 đường thẳng (d1), (d2), (d3) đồng quy.
Bài 34 trang 12 Sách bài tập Toán 9 Tập 2: Nghiệm chung của ba phương trình đã cho được gọi là nghiệm của hệ gồm ba phương trình ấy. Giải hệ phương trình là tìm nghiệm chung của tất cả các phương trình trong hệ. Hãy giải các hệ phương trình sau:
Bài giải:
Thay x = 3, y = 5 vào vế trái của phương trình (3) ta được:
5.3 – 2.5 = 15 – 10 = 5 (thỏa mãn)
Vậy (x; y) = (3; 5) là nghiệm của phương trình (3).
Hệ phương trình đã cho có nghiệm (x; ) = (3; 5)
Thay x = -3, y = 31/5 vào vế trái của phương trình (2), ta được:
-3. (-3) + 2.31/5 = 9 + 62/5 = 107/5 ≠ 22
Vậy (x; y) = (-3; 31/5) không phải là nghiệm của phương trình (2).
Hệ phương trình đã cho vô nghiệm.
Bài 1 trang 12 Sách bài tập Toán 9 Tập 2: Giải các hệ phương trình:
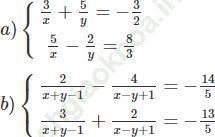
Bài giải:
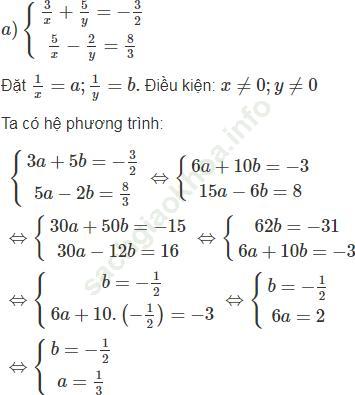
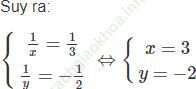
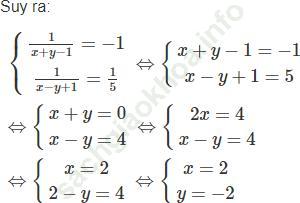
Hai giá trị x = 2; y = -2 thỏa mãn điều kiện bài toán.
Vậy hệ phương trình đã cho có một nghiệm (x; y) = (2; -2)
Bài 2 trang 12 Sách bài tập Toán 9 Tập 2: Hãy xác định hàm số bậc nhất thỏa mãn mỗi điều kiện sau:
a) Đồ thị hàm số đi qua hai điểm M (-3; 1) và N (1; 2)
b) Đồ thị hàm số đi qua hai điểm M (√ 2; 1) và N (3; 3√ 2 - 1)
c) Đồ thị đi qua điểm M (-2; 9) và cắt đường thẳng (d): 3x – 5y = 1 tại điểm có hoành độ bằng 2.
Bài giải:Hàm số bậc nhất có dạng y = ax + b (a ≠ 0)
a) Đồ thị hàm số y = ax + b đi qua M (-3; 1) và N (1; 2) nên tọa độ của M và N nghiệm đúng phương trình hàm số.
Điểm M: 1 = -3a + b
Điểm N: 2 = a + b
Hai số a và b là nghiệm của hệ phương trình:
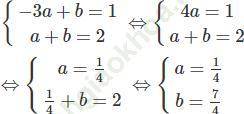
b) Đồ thị hàm số y = ax + b đi qua M (√ 2; 1) và N (3; 3√ 2 - 1) nên tọa độ của M và N nghiệm đúng phương trình hàm số.
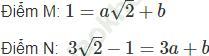
Hai số a và b là nghiệm của hệ phương trình:
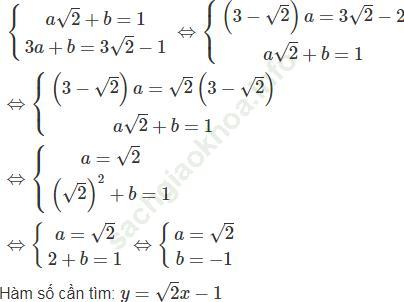
c) Điểm N nằm trên đường thẳng (d): 3x – 5y = 1 có hoành độ bằng 2 nên tung độ của N bằng: 3.2 - 5y = 1 ⇔ -5y = -5 ⇔ y = 1
Điểm N (2; 1)
Đồ thị hàm số y = ax + b đi qua M (-2; 9) và N (2; 1) nên tọa độ của M và N nghiệm đúng phương trình hàm số.
Điểm M: 9 = -2a + b
Điểm N: 1 =2a + b
Hai số a và b là nghiệm của hệ phương trình:
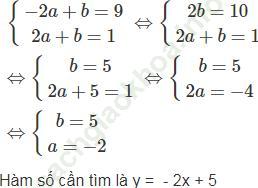
Bài 3 trang 13 Sách bài tập Toán 9 Tập 2: Giải hệ phương trình:
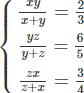
Bài giải:
Điều kiện: x ≠ -y; y ≠ -z; z ≠ -x
Từ hệ phương trình đã cho suy ra: x ≠ 0; y ≠ 0; z ≠ 0
Ta có hệ phương trình:
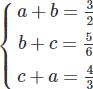
Cộng từng vế ba phương trình ta có:
Suy ra:
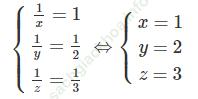
Vậy hệ phương trình đã cho có một nghiệm (x; y; z) = (1; 2; 3).