Bài 4: Đường thẳng song song và đường thẳng cắt nhau - trang 65 Sách bài tập Toán 9 Tập 1
Bài 4: Đường thẳng song song và đường thẳng cắt nhau
Bài 18 trang 65 Sách bài tập Toán 9 Tập 1: Cho hàm số y = ax + 3. Hãy xác định hệ số a trong mỗi trường hợp sau:
a. Đồ thị của hàm số song song với đường thẳng y = -2x
b. Khi x = 1 + √ 2 thì y = 2 + √ 2
Bài giải:a. Đồ thị của hàm số y = ax + 3 song song với đường thẳng y = -2x nên a = -2
b. Khi x = 1 + √ 2 thì y = 2 + √ 2
Ta có: 2 + √ 2 = a (1 + √ 2) + 3 ⇔ a (1 + √ 2) = √ 2 – 1
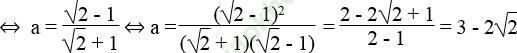
Vậy a = 3 - 2√ 2
Bài 19 trang 65 Sách bài tập Toán 9 Tập 1: Biết rằng với x = 4 thì hàm số y = 2x + b có giá trị là 5.
a. Tìm b.
b. Vẽ đồ thị của hàm số ứng với giá trị của b tìm được ở câu a.
Bài giải:a. Với x = 4 thì hàm số y = 2x + b có giá trị là 5, ta có:
5 = 2.4 + b ⇔ b = 5 – 8 ⇔ b = -3
b. Vẽ đồ thị hàm số y = 2x – 3
Cho x = 0 thì y = -3. Ta có: A (0; -3)
Cho y = 0 thì x = 1,5. Ta có: B (1,5; 0)
Đồ thị của hàm số y = 2x + 3 là đường thẳng đi qua hai điểm A, B
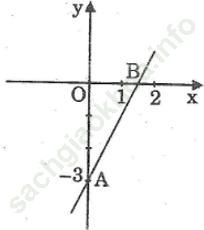
Bài 20 trang 66 Sách bài tập Toán 9 Tập 1: Tìm hệ số a của hàm số y = ax + a (1) biết rằng x = 1 + √ 2 thì y = 3 + √ 2
Bài giải:Thay x = 1 + √ 2; y = 3 + √ 2 vào hàm số (1) ta có:
3 + √ 2 = a (1 + √ 2) + 1 ⇔ a (1 + √ 2) = 2 + √ 2
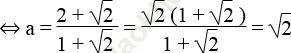
Vậy a = √ 2
Bài 21 trang 66 Sách bài tập Toán 9 Tập 1: Xác định hàm số y = ax + b biết đồ thị cắt trục tung tại điểm có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng -2.
Bài giải:Vì đồ thị hàm số y = ax + b cắt trục tung tại điểm có tung độ bằng 2 nên b=2
Vì đồ thị hàm số y = ax + 2 cắt trục hoành tại điểm có hoành độ bằng -2 nên tung độ của giao điểm bằng 0, ta có:
0 = a. (-2) + 2 ⇔ 2a = 2 ⇔ a = 1
Vậy hàm số đã cho là y = x + 2.
Bài 22 trang 66 Sách bài tập Toán 9 Tập 1: Xác định hàm số trong mỗi trường hợp sau, biết đồ thị của hàm số là đường thẳng đi qua gốc tọa độ:
a. Đi qua điểm A (3; 2)
b. Có hệ số a = 3
c. Song song với đường thẳng y = 3x + 1
Bài giải:Đồ thị hàm số đi qua gốc tọa độ có dạng y = ax.
a. Đồ thị hàm số đi qua điểm A (3; 2) nên tọa độ A nghiệm đúng phương trình hàm số.
Ta có: 2 = a. 3 ⇔ a = 2/3
Vậy hàm số đã cho là y = 2/3. x.
b. Vì a = √ 3 nên ta có hàm số y = √ 3 x
c. Đồ thị hàm số y = ax song song với đường thẳng y = 3x + 1 nên a = 3
Vậy hàm số đã cho là y = 3x.
Bài 23 trang 66 Sách bài tập Toán 9 Tập 1: Trên mặt phẳng tọa độ Oxy cho hai điểm A (1; 2), B (3; 4)
a. Tìm hệ số a của đường thẳng đi qua A và B
b. Xác định hàm số biết đồ thị của nó là đường thẳng đi qua A và B
Bài giải:Đường thẳng đi qua hai điểm A và B có dạng: y = ax + b
a. Đường thẳng đi qua hai điểm A và B nên tọa độ A và B nghiệm đúng phương trình.
Ta có: Tại A: 2 = a + b ⇔ b = 2 – a (1)
Tại B: 4 = 3a + b (2)
Thay (1) và (2) ta có: 4 = 3a + 2 – a ⇔ 2a = 2 ⇔ a = 1
Vậy hệ số a của đường thẳng đi qua A và B là 1.
b. Thay a = 1 vào (1) ta có: b = 2 – 1 = 1
Vậy phương trình đường thẳng AB là y = x + 1
Bài 24 trang 66 Sách bài tập Toán 9 Tập 1: Cho đường thẳng y = (k + 1)x + k (1)
a. Tìm giá trị của k để đường thẳng (1) đi qua gốc tọa độ
b. Tìm giá trị của k để đường thẳng (1) cắt trục tung tại điểm có tung độ bằng 1 - √ 2
c. Tìm giá trị của k để đường thẳng (1) song song với đường thẳng y = (√ 3 + 1)x + 3
Bài giải:a. Đường thẳng y = (k + 1)x + k có dạng là hàm số bậc nhất đi qua gốc tọa độ nên k = 0
Vậy hàm số có dạng: y = x
b. Đường thẳng y = ax + b cắt trục tung tại điểm có tung độ bằng b, mà đường thẳng y = (k + 1)x + k cắt trục tung tại điểm có tung độ bằng 1 - √ 2 nên k = 1 - √ 2.
c. Đường thẳng y = (k + 1)x + k song song với đường thẳng y = (√ 3 +1)x+3 khi và chỉ khi:
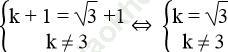
Vậy hàm số có dạng: y = (√ 3 + 1)x + √ 3.
Bài 1 trang 66 Sách bài tập Toán 9 Tập 1: Đường thẳng y = kx + 1/2 song song với đường thẳng 
khi k có giá trị:
Bài giải:
Đáp án đúng là: D. -5/7
Bài 2 trang 66 Sách bài tập Toán 9 Tập 1: Đường thẳng 
và đường thẳng 
song song với nhau khi m có giá trị là:
Bài giải:
Đáp án đúng là C. -1/19
Bài 3 trang 67 Sách bài tập Toán 9 Tập 1: Hai đường thẳng y = (2m + 1)x - 2/3 và y = (5m – 3)x + 3/5 cắt nhau khi m có giá trị khác với giá trị sau:
Bài giải:
Đáp án đúng là B. 4/3
Bài 4 trang 67 Sách bài tập Toán 9 Tập 1: Cho hàm số
a) Tìm giá trị của k để đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 2√ 3.
b) Tìm giá trị của k để đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 1.
c) Chứng minh rằng, với mọi giá trị k ≥ 0, các đường thẳng (d) luôn đi qua một điểm cố định. Hãy xác định tọa độ của điểm cố định đó.
Bài giải:a) Để biểu thức ở vế phải xác định thì k ≥ 0.
√ k + √ 3 = 2√ 3 ⇔ √ k = √ 3 ⇒ k = 3.
b) Đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 1 khi:
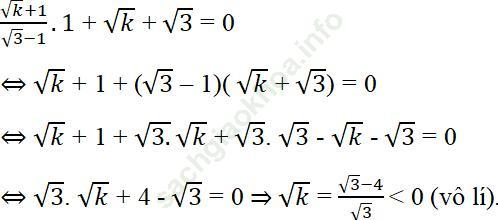
Vậy đường thẳng (d) không cắt trục hoành tại điểm có hoành độ bằng 1 với mọi giá trị của k ≥ 0.
Nói các khác, đường thẳng 
không bao giờ cắt trục hoành tại điểm có hoành độ bằng 1.
c) Gọi điểm cố định mà các đường thẳng (d) đều đi qua P (xo, yo).
Ta có:
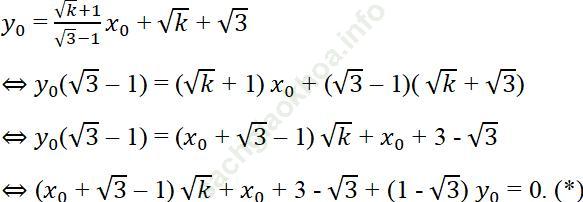
Phương trình (*) nghiệm đúng với mọi giá trị không âm của √ k, do đó ta có:
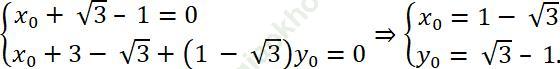
Vậy, với k ≥ 0, các đường thẳng (d) đều đi qua điểm cố định P (1- √ 3; √ 3 – 1).
Bài trước: Bài 3: Đồ thị của hàm số y = ax + b (trang 64 Sách bài tập Toán 9 Tập 1) Bài tiếp: Bài 5: Hệ số góc của đường thẳng y = ax + b (trang 67 Sách bài tập Toán 9 Tập 1)