Bài 6: Hệ thức Vi-ét và ứng dụng - trang 57 Sách bài tập Toán 9 Tập 2
Bài 35 trang 57 Sách bài tập Toán 9 Tập 2: Giải phương trình rồi kiểm nghiệm hệ vi-ét:
a. 5x2 + 2x -16 =0
b. 3x2 -2x -5 =0
Bài giải:
a) Phương trình 5x2 + 2x -16 =0 có hệ số a = 5; b = 2; c = -16
Ta có: Δ ' = 12 - 5 (-16) = 1 + 80 = 81 > 0
√ Δ ' = √ 81 = 9
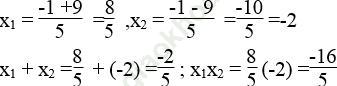
b) Phương trình 3x2 -2x -5 =0 có hệ số a = 3; b = -2; c = -5
Ta có: Δ '= (-1)2 -3 (-5) = 1 + 15 =16 > 0
√ Δ ' = √ 16 =4
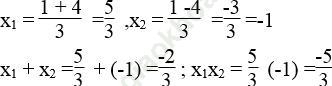
c) Phương trình ![]()
Δ '= 32 - 1 (-16) = 9 +16 = 25 > 0
√ Δ ' = √ 25 =5
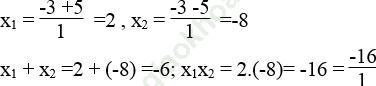
d) Phương trình ![]()
Ta có: Δ '= (-3)2 -1.4 = 9 -4 =5 > 0
√ Δ ' = √ 5
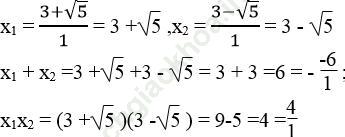
Bài 36 trang 57 Sách bài tập Toán 9 Tập 2: Không giải phương trình, dùng hệ thức Vi-ét, hãy tính tổng và tích các nghiệm của mỗi phương trình
a. 2x2 – 7x +2 =0
b. 5x2 +2x -16 =0
c. (2 - √ 3)x2+4x +2 +√ 2 =0
d. 1,4x2 -3x +1,2 =0
e. 5x2 +x +2 =0
Bài giải:a) Ta có: Δ = (-7)2 - 4.2.2 = 49 - 16 = 33 > 0
Phương trình có 2 nghiệm phân biệt. Theo hệ thức Vi-ét, ta có:
x1 + x2 = -b/a = 7/2;
x1x2 = c/a = 2/2 = 1
b) c = -16 suy ra ac < 0
Phương trình có 2 ghiệm phân biệt.
Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =-2/5;
x1x2 =c/a =-16/5
c) Ta có: Δ ’ = 22 – (2 -√ 3)(2 + √ 2) =4 -4 - 2√ 2 +2√ 3 +√ 6
= 2√ 3 - 2√ 2 +√ 6 > 0
Phương trình có 2 nghiệm phân biệt.
Theo hệ thức Vi-ét, ta có:
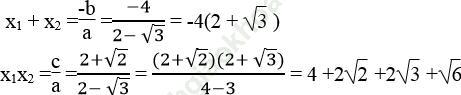
d) Ta có: Δ = (-3)2 -4.1,4.1,2 =9 – 6,72 =2,28 > 0
Phương trình có 2 ghiệm phân biệt. Theo hệ thức Vi-ét, ta có:
x1 + x2 = -b/a = 3/ (1.4) = 30/14 = 15/7;
x1x2 = c/a = (1.2)/ (1.4) = 12/14 = 6/7
e) PT: 5x2 +x +2 =0
Ta có: Δ = 12 -4.5.2 = 1 - 40 = -39 < 0 => pt vô nghiệm
Bài 37 trang 57 Sách bài tập Toán 9 Tập 2: Tính nhẩm nghiệm của các phương trình:
a. 7x2 -9x +2=0 b. 23x2 -9x -32=0
c. 1975x2 + 4x -1979 =0 d. (5 +√ 2)x2 + (5 - √ 2)x -10 =0
a) Phương trình:
7x2 - 9x + 2 = 0 có hệ số a = 7, b = -9, c = 2
Ta có: a + b + c = 7 + (-9) + 2 = 0
Suy ra nghiệm của phương trình là:
x1 = 1
x2 = c/a = 2/7
b) Phương trình 23x2 - 9x – 32 = 0 có hệ số a = 23, b = -9, c = -32
Ta có: a –b +c =23 – (-9) + (-32) =0
Suy ra nghiệm của phương trình là x1= -1, x2 = -c/a = - (-32)/23 = 32/23
c. Phương trình 1975x2 + 4x -1979 = 0 có hệ số a = 1975, b = 4, c = -1979
Ta có: a +b +c =1975 + 4 + (-1979) = 0
Suy ra nghiệm của phương trình là x1 = 1, x2 = c/a = -1979/1975
d) Phương trình (5 +√ 2)x2 + (5 - √ 2)x -10 = 0 có hệ số
a =5 +√ 2, b = 5 - √ 2, c = -10
Ta có: a +b +c =5 +√ 2 +5 - √ 2 + (-10)=0
Suy ra nghiệm của phương trình là x1 = 1, x2 = ca = (-10)/ (5+ √2)
e. Phương trình ![]() ⇔ 2x√ - 9x + 11 = 0 có hệ số a = 2, b = 9, c = -11
⇔ 2x√ - 9x + 11 = 0 có hệ số a = 2, b = 9, c = -11
Ta có: a –b +c =2 – (-9) + (-11) =0
Suy ra nghiệm của phương trình là x1=-1, x2 = -c/a = - (-11)/2 =11/2
f. Phương trình 31,1x2 – 50,9x + 19,8 = 0 ⇔ 311x2 – 509x +198 = 0 có hệ số a = 311, b = -509, c = 198
Ta có: a + b + c = 311 + (-509) + 198 = 0
Suy ra nghiệm của phương trình là x1 = 1, x2 = c/a = 198/311
Bài 38 trang 57 Sách bài tập Toán 9 Tập 2: Dùng hệ thức Vi-ét để tính nhẩm nghiệm của các phương trình:
a. x2-6x +8=0
b. x2 -12x + 32 =0
c. x2 +6x +8 =0
d. x2 -3x -10 =0
e. x2 +3x -10 =0
Bài giải:a. Ta có: Δ ’ = (-3)2 -1.8=9 -8 =1 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
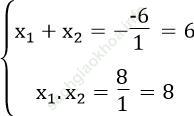
Giải ra ta được x1 =2, x2 =4
b. Ta có: Δ ’ = (-6)2 -1.32 = 36 - 32 = 4 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
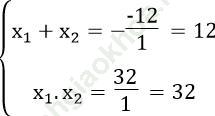
Giải ra ta được x1 =4, x2 =8
c. Ta có: Δ ’ = 32 -1.8=9 -8 =1 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
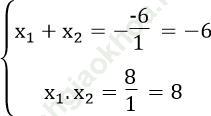
Giải ra ta được x1 =-2, x2 =-4
d. Ta có: Δ = (-3)2 -4.1. (-10)=9 +40 =49 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
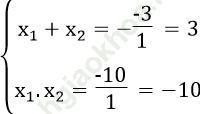
Giải ra ta được x1 =-2, x2 =5
e. Ta có: Δ = 32 -4.1. (-10)=9 +40 =49 > 0
Phương trình có 2 nghiệm phân biệt
Theo hệ thức Vi-ét ta có:
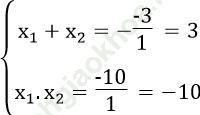
Bài 39 trang 57 Sách bài tập Toán 9 Tập 2:
a. Chứng tỏ rằng phương trình 3x2 +2x -21 =0 có một nghiệm là -3. Hãy tìm nghiệm kia
b. Chứng tỏ rằng phương trình -4x2 -3x +115=0 có một nghiệm là 5. Hãy tìm nghiệm kia
Bài giải:a. Thay x = -3 vào vế trái của phương trình, ta có:
3. (-3)2+2 (-3) -21 =27 – 6 -21 =0
Vậy = -3 là nghiệm của phương trình 3x2 +2x -21 =0
Theo hệ thức vi-ét ta có: x1x2 = c/a = -21/3 = -7 ⇒ x2 = -7/x1 = -7/-3 = 7/3
Vậy nghiệm còn lại là x = 7/3
b. Thay x = 5 vào vế trái của phương trình, ta có:
-4.52 -3.5 +115 =-100 -15 +115 =0
Vậy x = 5 là nghiệm của phương trình -4x2 -3x + 115=0
Theo hệ thức Vi-ét ta có: x1x2 = c/a = 115/-4 ⇒ 5x2 = -115/4 ⇒ x2 = -23/4
Vậy nghiệm còn lại là x = -23/4
Bài 40 trang 57 Sách bài tập Toán 9 Tập 2: Dùng hệ thức vi-ét để tìm nghiệm x2 của phương trình rồi tìm giá trị của m trong mỗi trường hợp sau:
a. Phương trình x2 +mx -35 =0 có nghiệm x1 =7
b. Phương trình x2 -13x+m=0 có nghiệm x1 =12,5
c. Phương trình 4x2 +3x – m2 +3m =0 có nghiệm x1 =-2
d. Phương trình 3x2 -2 (m -3)x +5 =0 có nghiệm x1 =13
Bài giải:a. Theo hệ thức Vi-ét ta có: x1x2 = -35
Suy ra 7x2 = -35 ⇔ x2 = -5
Cũng theo hệ thức Vi-ét ta có: x1 + x2 =-m
Suy ra: m= -7 +5 ⇔ m = -2
Vậy với m = -2 thì phương trình x2 + mx - 35 = 0 có hai nghiệm x1 = 7, x2 = -5
b. Theo hệ thức Vi-ét ta có: x1 + x2 =13
Suy ra 12,5 + x2 = 13 ⇔ x2 = 0,5
Cũng theo hệ thức Vi-ét ta có: x1x2 = m
Suy ra: m = 12,5.0,5 ⇔ m = 6,25
Vậy với m = 6,25 thì phương trình x2 - 13x + m = 0 có hai nghiệm
x1 = 12,5, x2 = 0,5
c) Theo hệ thức Vi-ét ta có: x1 + x2 = - 3/4
Suy ra: -2 + x2 = - 3/4 ⇔ x2 = -3/4 + 2 = 5/4
Cũng theo hệ thức Vi-ét ta có: x1x2 = (-m2+3m)/4
Suy ra: -2.5/4 = (-m2+3m)/4 ⇔ m2 -3m -10 =0
Δ = (-3)2 -4.1. (-10) =9+40 =49
√ Δ =√ 49 =7
m1 = (3 +7)/ (2.1) =5; m2 = (3 -7)/ (2.1) =-2
Vậy với m = 5 hoặc m = -2 thì phương trình 4x2 +3x – m2 +3m = 0 có hai nghiệm x1 = -2, x2 = 5/4
d) Theo hệ thức Vi-ét ta có: x1x2 = 5/3
Suy ra: 1/3. x2 = 5/3 ⇔ x2 = 5/3: 1/3 = 5/3.3 = 5
cũng theo hệ thức Vi-ét ta có: x1 + x2 = [2 (m -3)]/3
Suy ra: 1/3 + 5 = [2 (m -3)]/3 ⇔ 2 (m -3) =16 ⇔ m - 3 = 8 ⇔ m = 11
Vậy với m = 11 thì phương trình 3x2 -2 (m -3)x +5 =0 có hai nghiệm x1 = 13, x2 = 5
Bài 41 trang 58 Sách bài tập Toán 9 Tập 2: Tìm hai số u và v trong mỗi trường hợp sau:
a. u +v =14, uv =40 b. u +v =-7, uv =12
c. u +v =-5, uv =-24 d. u +v =4, uv =19
e. u – v =10, uv =24 f. u2 + v2 =85, uv =18
Bài giải:a) Hai số u và v với u +v =14 và uv =40 nên nó là nghiệm của phương trình x2 -14x + 40=0
Δ ’= (-7)2 – 1.40=49 -40 =9 > 0
√ Δ ' = √ 9 =3
Vậy u=10, v=4 hoặc u = 4, v = 10
b. Hai số u và v với u +v =-7 và uv =12 nên nó là nghiệm của phương trình x2 +7x + 12=0
Δ = (7)2 – 4.1.12=49 -48=1 > 0
√ Δ =√ 1 =1
Vậy u=-3, v=-4 hoặc u=-4, v=-3
c. Hai số u và v với u +v =-5 và uv =-24 nên nó là nghiệm của phương trình x2 +5x -24 =0
Δ = (5)2 – 4.1. (-24)= 25 +96=121 > 0
√ Δ = √ 121 =11
Vậy u = 3, v = -8 hoặc u = -8, v = 3
d. Hai số u và v với u +v =4 và uv =19 nên nó là nghiệm của phương trình x2 - 4x +19 = 0
Δ ’= (-2)2 – 1.19= 4 - 19=-15 < 0
Phương trình vô nghiệm nên không có giá trị nào của u và v thỏa mãn điều kiện bài toán
e. Hai số u và v với u – v =10 suy ra: u + (- v) = 10 và uv = 24 suy ra u (-v) = -24 nên nó là nghiệm của phương trình x2 -10x -24 =0
Δ ’= (-5)2 – 1. (-24)= 25 +24=49 > 0
√ Δ ' = √ 49 =7
Vậy u = 12, -v = -2 hoặc u = -2, -v = 12 suy ra u = 12, v = 2 hoặc u = -2, v = -12
f. Hai số u và v với u2 + v2 =85 và uv =18 suy ra: u2v2=324 nên u2 và v2 là nghiệm của phương trình x2 -85x +324 =0
Δ = √ (-85)2 – 4.1.324= 7225 – 1296=5929 > 0
√ Δ = √ 2959 =77
Ta có: u2 =81, v2 =4 suy ra: u =±9, v=± 2
hoặc u2 =4, v2 =81 suy ra: u =±2, v=± 9
Vậy nếu u=9 thì v=2 hoặc u=-9, v=-2
nếu u=2 thì v=9 hoặc u= -2, v=-9
Bài 42 trang 58 Sách bài tập Toán 9 Tập 2: Lập phương tình có hai nghiệm là hai số được cho mỗi trường hợp sau:
a. 3 và 5 b. -4 và 7
c. -5 và 1/3 d. 1,9 và 5,1
e. 4 và 1 -√ 2 f. 3 - √ 5 và 3 + √ 5
Bài giải:a) Hai số 3 và 5 là nghiệm của phương trình:
(x -3)(x -5) = 0 ⇔ x2 -3x -5x +15 =0 ⇔ x2 -8x +15 =0
b. Hai số 3 và 5 là nghiệm của phương trình:
(x +4)(x -7) = 0 ⇔ x2 +4x -7x -28 =0 ⇔ x2 -3x -28 =0
c. Hai số -5 và 1/3 là nghiệm của phương trình:
(x +5)(x -1/3)=0 ⇔ x2 +5x -1/3 x -5/3 =0 ⇔ 3x2 +14x - 5 =0
d. Hai số 1,9 và 5,1 là nghiệm của phương trình:
(x - 1,9) (x -5,1)=0 ⇔ x2 - 1,9x - 5,1x + 9,69 = 0
⇔ x2 -7x + 9,69 = 0
e. Hai số 4 và 1 -√ 2 là nghiệm của phương trình:
(x - 4)[x – (1 -√ 2)] =0 ⇔ (x -4)(x -1 +√ 2) =0
⇔ x2 - x +√ 2 x -4x +4 - 4√ 2 =0
⇔ x2 – (5 -√ 2)x +4 - 4√ 2 =0
f. Hai số 3 - √ 5 và 3 + √ 5 là nghiệm của phương trình:
[x – (3 - √ 5)] [x – (3 + √ 5)] = 0
⇔ x2 – (3 + √ 5)x - (3 - √ 5)x + (3+ √ 5)(3 - √ 5) =0
⇔ x2 -6x +4 =0
Bài 43 trang 58 Sách bài tập Toán 9 Tập 2: Cho phương trình x2 + px – 5 = 0 có hai nghiệm x1 và x2. Hãy lập phương trình có hai nghiệm là hai số được cho trong mỗi trường hợp sau:
a. –x1 và –x2
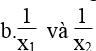
a) Phương trình x2+px -5=0 có hai nghiệm x1 và x2 nên theo hệ thức vi-ét ta có:
x1 + x2 = -p/1 = -p; x1x2 =-5/1 =-5 (1)
Hai số –x1 và –x2 là nghiệm của phương trình:
[x – (-x1)] [x – (-x2)] =0
⇔ x2 – (-x1x) – (-x2x) + (-x1) (-x2) =0
⇔ x2 + (x1 + x2x + x1x2) =0 (2)
Từ (1) và (2) ta có phuơng trình cần tìm là x2 – px -5 =0

Bài 44 trang 58 Sách bài tập Toán 9 Tập 2: Cho phương trình x2 -6x +m=0
Tính giá trị của m biết rằng phương trình có hai nghiệm x1,x2 thỏa mãn điều kiện x1 –x2 = 4
Bài giải:Phương trình x2 - 6x + m = 0 có hai nghiệm x1 và x2 nên theo hệ thức Vi-ét ta có:
x1 + x2 =- (-6)/1 = 6
Kết hợp với điều kiện x1 – x2 =4 ta có hệ phương trình:
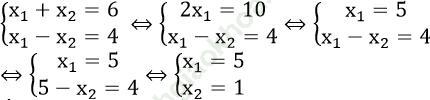
Áp dụng hệ thức vi-ét vào phương trình x2 -6x +m=0 ta có:
x1x2 = m1 = m. Suy ra: m = 5.1 = 5
Vậy m =5 thì phương trình x2 -6x +m=0 có hai nghiệm x1 và x2 thỏa mãn điều kiện x1 – x2 =4
Bài 1 trang 58 Sách bài tập Toán 9 Tập 2:
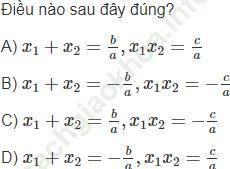
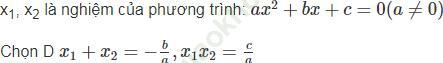
Bài 2 trang 58 Sách bài tập Toán 9 Tập 2: Giả sử x1, x2 la hai nghiệm của phương trình x2 + px + q = 0. Hãy lập một phương trình bậc hai có hai nghiệm x1 + x2, x1x2.
Bài giải:Giả sử x1, x2 là nghiệm của phương trình: x2 + px + q = 0
Theo hệ thức Vi-ét ta có: x1 + x2 = - p/1 = - p; x1x2 = q/1 = q
Phương trình có hai nghiệm là x1 + x2 và x1x2 tức là phương trình có hai nghiệm là –p và q.
Hai số -p và q là nghiệm của phương trình.
(x + p)(x - q) = 0 ⇔ x2 - qx + px - pq = 0 ⇔ x2 + (q - p)x - pq = 0
Phương trình cần tìm: x2 + (p - q)x - pq = 0
Bài 3 trang 58 Sách bài tập Toán 9 Tập 2:

Bài giải:
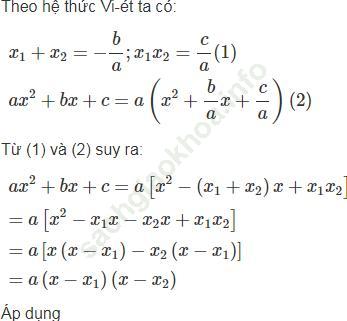

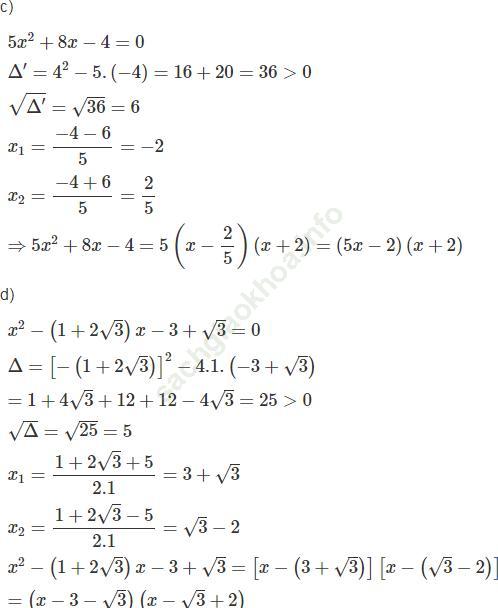
Bài 4 trang 59 Sách bài tập Toán 9 Tập 2: Cho phương trình
(SBT)
a) Tìm giá trị của m để phương trình có nghiệm.
b) Khi phương trình có nghiệm x1, x2, hãy tính tổng S và tích P của hai nghiệm theo m.
c) Tìm hệ thức giữa S và P sao cho trong hệ thức này không có m.
Bài giải:
