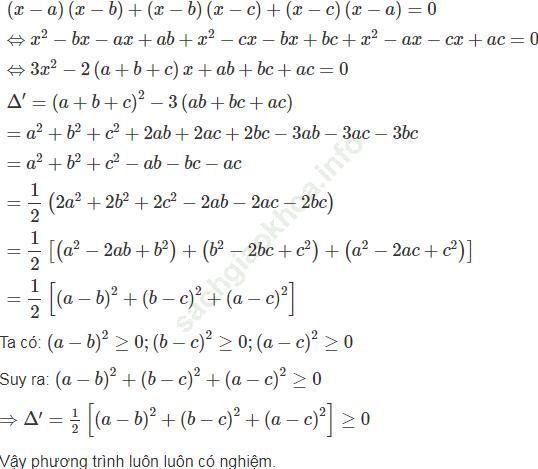Bài 5: Công thức nghiệm thu gọn - trang 55 Sách bài tập Toán 9 Tập 2
Bài 5: Công thức nghiệm thu gọn
Bài 27 trang 55 Sách bài tập Toán 9 Tập 2: Xác định a, b’, c trong mỗi phương trình rồi giải phương trình bằng công thức nghiệm thu gọn:
a. 5x2 – 6x -1 = 0
b. -3x2 + 14x - 8 = 0
c. -7x2 + 4x = 3
d. 9x2 + 6x + 1 = 0
Bài giải:a. Phương trình 5x2 – 6x -1 = 0 có hệ số a = 5, b’ = -3, c = -1
Ta có: Δ ’ = b’2 – ac = (-3)2 -5. (-1) = 9 + 5 = 14 > 0
√ Δ ' =√ 14
Phương trình có hai nghiệm phân biệt:
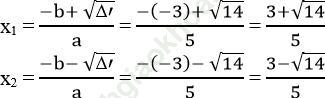
b. Phương trình -3x2+ 14x - 8 = 0 có hệ số a = -3, b’= 7, c = -8
Ta có: Δ ' = b’2 – ac = 72 – (-3). (-8) = 49 – 24 > 0
√ Δ ' = √ 25 = 5
Phương trình có 2 nghiệm phân biệt:
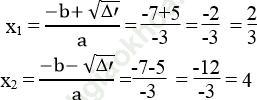
c. Phương trình -7x2 +4x=3 ⇔ 7x2 -4x+3 = 0 có hệ số a=7, b’=-2, c=3
Ta có: Δ ’ = b’2 – ac = (-2)2 -7.3 = 4- 21= -17 < 0
Vậy phương trình vô nghiệm
d. Phương trình 9x2 +6x+1 =0 có hệ số a=9, b’=3, c=1
Ta có: Δ ’ = b’2 – ac = 32 -9.1 = 9 - 9 = 0
Phương trình có nghiệm kép:
x1 = x2 = -b'/a =-3/9 =-1/3
Bài 28 trang 55 Sách bài tập Toán 9 Tập 2: Với những giá trị nào của x thì giá trị của hai biểu thức sau bằng nhau?
a. x2 +2 + 2√ 2 = 2 (1+√ 2)x
b. √ 3 x2 + 2x -1 = 2√ 3 x +3
c. -2√ 2 x – 1 =√ 2 x2 + 2x +3
d. x2 - 2√ 3 x - √ 3 = 2x2 +2x +√ 3
e. √ 3 x2 + 2√ 5 x - 3√ 3 = -x2 - 2√ 3 x +2√ 5 +1
Bài giải:a, Ta có: x2 +2 + 2√ 2 = 2 (1+2)x ⇔ x2 - 2 (1+√ 2)x +2 +2√ 2 = 0
Δ ' = b’2 – ac = [- (1+√ 2)]2- 1 (2+2√ 2)
= 1 + 2√ 2 +2 -2 -2√ 2 =1 > 0
√ Δ ' = √ 1 =1
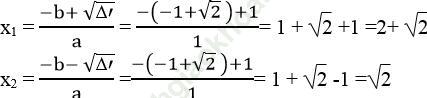
Vậy với x= 2+ √ 2 hoặc x =√ 2 thì giá trị của hai biểu thức trên bằng nhau
b. Ta có: √ 3 x2 + 2x -1 = 2√ 3 x +3 ⇔ 3 x2 + 2x - 2√ 3 x -3 -1 = 0
⇔ √ 3 x2 + (2 - 2√ 3)x -4 =0 ⇔ √ 3 x2 + 2 (1 - √ 3)x -4 = 0
Δ ' = b’2 – ac= (1- √ 3)2 - √ 3 (-4) =1 - 2√ 3 +3 +4√ 3
= 1 + 2√ 3 +3 = (1 + 3)2 > 0

Vậy với x= 2 hoặc x = (-2√3)/3 thì giá trị của hai biểu thức trên bằng nhau
c, Ta có: -2√ 2 x – 1 =√ 2 x2 + 2x +3 ⇔ √ 2 x2 +2x + 3 + 2√ 2 x + 1=0
⇔ √ 2 x2 + 2 (1 + √ 2)x +4 =0
Δ ' = b’2 – ac= (1+ √ 2)√ - √ 2.4= 1+2√ 2 +2 - 4√ 2
= 1-2√ 2 +2 = (√ 2 -1)√ > 0
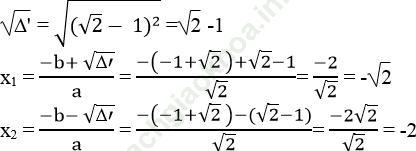
Vậy với x= -√ 2 hoặc x = -2 thì giá trị của hai biểu thức trên bằng nhau
d. Ta có: x2 - 2√ 3 x - √ 3 = 2x2 +2x +√ 3
⇔ x2 - 2√ 3 x - √ 3 - 2x2 -2x - √ 3 =0
⇔ x2 +2x +2√ 3 x +2√ 3 =0
⇔ x2 + 2 (1 +√ 3)x + 2√ 3 =0
Δ ' = b’2 – ac= (1+ √ 3)√ – 1.2√ 3 = 1 + 2√ 3 +√ 3 -2√ 3 =4> 0
√ Δ ' = √ 4 =2
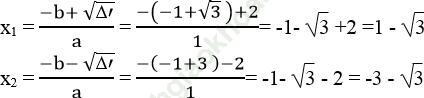
Vậy với x=1 - √ 3 hoặc x = - 3 - √ 3 thì giá trị của hai biểu thức trên bằng nhau
e. Ta có: √ 3 x2 + 2√ 5 x - 3√ 3 = -x2 - 2√ 3 x +2√ 5 +1
⇔ √ 3 x2 + 2√ 5 x - 3√ 3 + x2 + 2√ 3 x - 2√ 5 – 1= 0
⇔ (√ 3 +1)x2 + (2√ 5 + 2√ 3)x -3√ 3 - 2√ 5 – 1= 0
⇔ (√ 3 +1)x2 + 2 (√ 5 + √ 3)x -3√ 3 - 2√ 5 – 1= 0
Δ ' = b’√ – ac= (√ 3 + √ 5)√ – (√ 3 +√ 1) (-3√ 3 - 2√ 5 – 1)
= 5 + 2√ 15 +3+9 +2√ 15 + √ 3 +3√ 3 +2√ 5 + 1
=18 +4√ 15 +4√ 3 +2√ 5
= 1 + 12 + 5 + 2.2√ 3 + 25 + 2.2√ 3. √ 5
= 1 + (2√ 3)√ + (√ 5)√ + 2.1.2√ 3 +2.1. √ 5 + 2.2√ 3. √ 5
= (1 +2√ 3 +√ 5)√ > 0

Bài 29 trang 55 Sách bài tập Toán 9 Tập 2: Một vận động viên bơi lội nhảy cầu (xem hình dưới). Khi nhảy độ cao h từ người đó đến mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức: h= - (x -1)2 +4. Hỏi cách x bằng bao nhiêu:
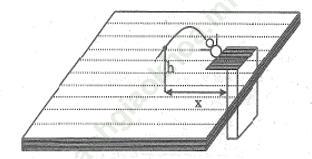
a. Khi vận động viên ở độ cao 3m?
b. Khi vận động viên chạm mặt nước?
Bài giải:Khi vận động viên ở độ cao 3m nghĩa là h =3m
Ta có: 3 =- (x – 1)2 + 4 ⇔ (x – 1)2 – 1=0 ⇔ x2 – 2x = 0
⇔ x (x – 2) = 0 ⇔ x=0 hoặc x – 2 =0 ⇔ x = 0 hoặc x = 2
Vậy x = 0m hoặc x = 2m
Khi vận động viên chạm mặt nước nghĩa là h = 0m
Ta có: 0 = - (x – 1)2 + 4 ⇔ x2 -2x -3 =0
Δ ' = b’2 – ac = (-1)2 -1. (-3) =1 +3 = 4 > 0
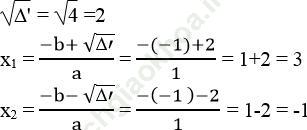
Vì khoảng cách không thể mang giá trị âm nên x=3m
Bài 30 trang 56 Sách bài tập Toán 9 Tập 2: Tính gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai):
a. 16x2 – 8x +1=0 b. 6x2 – 10x -1 =0
c. 5x2 +24x +9 =0 d. 16x2 – 10x +1 =0
Bài giải:a) 16x2 – 8x +1=0
Ta có: Δ ' = (-4)2 – 16.1 = 16 -16 =0
Phương trình có nghiệm kép:

c) 5x2 +24x +9 =0
Ta có: Δ ' =122 -5.9 =144 +45 =99 > 0
√ Δ ' = √ 99 =3√ 11
Phương trình có 2 nghiệm phân biệt:

Bài 31 trang 56 Sách bài tập Toán 9 Tập 2: Với giá trị nào của x thì giá trị của hai hàm số bằng nhau?
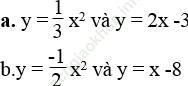
Bài giải:

Bài 32 trang 56 Sách bài tập Toán 9 Tập 2: Với giá trị nào của m thì:
a. Phương trình 2x2 – m2x +18m = 0 có một nghiệm x = -3
b. Phương trình mx2 – x – 5m2 = 0 có một nghiệm x = -2
Bài giải:a) Thay x=-3 vào phương trình 2x2 – m2x +18m =0 ta được:
2 (-3)2 - m2(-3) + 18m =0 ⇔ 3m2 +18m+18 =0
⇔ m2 + 6m +6 = 0
Δ ' = 32 -1.6 = 9 -6 =3 > 0
√ Δ ' = √ 3
Phương trình có 2 nghiệm phân biệt:
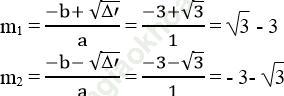
Vậy với m = 3 - 3 hoặc m =- 3- 3 thì phương trình đã cho có nghiệm x= -3
b) Thay x = -2 vào phương trình mx2 – x – 5m2 = 0 ta được:
m (-2)2 – (-2) – 5m2=0 ⇔ 5m2 – 4m -2 =0
Δ ' = (-2)2 -5. (-2) = 4+10 = 14 > 0
√ Δ ' = √ 14
Phương trình có 2 nghiệm phân biệt:

Bài 33 trang 56 Sách bài tập Toán 9 Tập 2: Với giá trị nào của m thì các phương trình sau có 2 nghiệm phân biệt
a. x2 – 2 (m+3)x + m2 + 3 = 0
b. (m+1)x2 + 4mx + 4m - 1 = 0
Bài giải:a. x2 – 2 (m+3)x + m2+3=0 (1)
Ta có: Δ ' = [- (m+3)]2 -1. (m2 +3) = m2 + 6m + 9 – m2 - 3
= 6m +6
Phương trình (1) có 2 nghiệm phân biệt khi và chỉ khi:
Δ ' > 0 ⇔ 6m + 6 > 0 ⇔ 6m > -6 ⇔ m > -1
Vậy m > -1 thì phương trình đã cho có 2 nghiệm phân biệt
b. (m+1)x2+4mx+4m -1 =0 (2)
Ta có: Δ ' = (2m)2 – (m +1)(4m -1) = 4m2 – 4m2 + m – 4m +1
= 1 – 3m
Phương trình (2) có 2 nghiệm phân biệt khi và chỉ khi:
*m +1 ≠ 0 ⇔ m ≠ -1
và *Δ ' > 0 ⇔ 1 -3m > 0 ⇔ 3m < 1 ⇔ m < 1/3
Vậy m < 1/3 và m ≠ -1 thì phương trình đã cho có 2 nghiệm phân biệt
Bài 34 trang 56 Sách bài tập Toán 9 Tập 2: Với giá trị nào của m thì các phương trình sau có nghiệm kép
a. 5x2 + 2mx – 2m +15 =0
b. mx2 – 4 (m -1)x -8 =0
Bài giải:a. 5x2 + 2mx – 2m +15 =0 (1)
Ta có: Δ '=m2 – 5. (-2m +15) = m2 +10m -75
Phương trình (1) có nghiệm kép khi và chỉ khi:
Δ '= 0 ⇔ m2 + 10m – 75 = 0
Δ 'm = 52 -1. (-75) = 25 +75 = 100 > 0
√ (Δ 'm) = √ 100 =10
Phương trình có 2 nghiệm phân biệt:
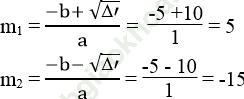
Vậy m =5 hoặc m=-15 thì phương trình đã cho có nghiệm kép
b. mx2 – 4 (m -1)x -8 =0 (2)
Phương trình (2) có nghiệm kép khi và chỉ khi: m≠ 0 và Δ '=0
Ta có: Δ '= [-2 (m-1)]2 – m (-8)=4 (m2 -2m +1) +8m
=4m2– 8m +4 +8m = 4m2 +4
Vì 4m2 +4 luôn luôn lớn hơn 0 nên Δ ' không thể bằng 0. Vậy không có giá trị nào của m để phương trình có nghiệm kép
Bài 1 trang 56 Sách bài tập Toán 9 Tập 2: Giả sử x1, x2 là hai nghiệm của phương trình bậc hai ax2 + bx + c = 0 có ∆’ = 0. Điều nào sau đây là đúng?
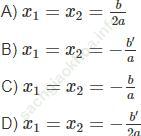
Giả sử x1, x2 là hai nghiệm của phương trình bậc hai ax2 + bx + c = 0 có ∆’ = 0
Chọn B
Bài 2 trang 56 Sách bài tập Toán 9 Tập 2: Tìm mối liên hệ giữa a, b, c để phương trình (b2 + c2)x2 - 2acx + a2 - b2 = 0 có nghiệm.
Bài giải:Hoặc b ≠ 0 hoặc c ≠ 0 phương trình có:

Bài 3 trang 56 Sách bài tập Toán 9 Tập 2: Chứng tỏ rằng phương trình (x - a)(x - b) + (x - b)(x - c) + (x - c)(x - a) = 0 luôn có nghiệm
Bài giải: