Bài 2: Căn thức bậc hai và hằng đẳng thức - trang 7 Sách bài tập Toán 9 Tập 1

Bài 2: Căn thức bậc hai và hằng đẳng thức

Bài 12 trang 7 Sách bài tập Toán 9 Tập 1: Tìm x để căn thức sau có nghĩa:

Bài giải:

a. Ta có: có nghĩa khi và chỉ khi:

-2x + 3 ≥ 0 ⇒ -2x ≥ -3 ⇒ x ≤ 3/2

b. Ta có: có nghĩa khi và chỉ khi:

2/x² ≥ 0 ⇒ x² > 0 ⇒ x ≠ 0

c. Ta có: có nghĩa khi và chỉ khi:

d. Ta có: x² ≥ 0 với mọi x nên x² + 6 > 0 với mọi x

Suy ra < 0 với mọi x

Vậy không có giá trị nào của x để có nghĩa.

Bài 13 trang 7 Sách bài tập Toán 9 Tập 1: Rút gọn rồi tính:

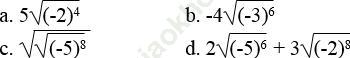
Bài giải:

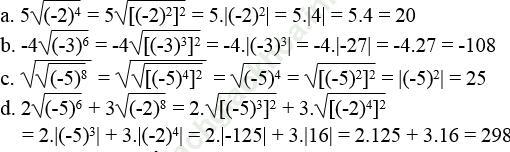
Bài 14 trang 7 Sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức sau:

Bài giải:

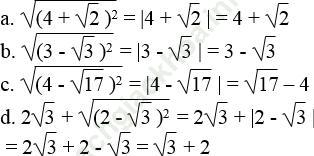
Bài 15 trang 7 Sách bài tập Toán 9 Tập 1: Chứng minh:

Bài giải:

a. Ta có:

VT = 9 + 4√ 5 = 4 + 2.2√ 5 + 5 = 2² + 2.2√ 5 + (√ 5)² = (2 + √ 5)²

Vế trái bằng vế phải nên đẳng thức được chứng minh.

b. Ta có:

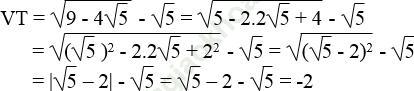
Vế trái bằng vế phải nên đẳng thức được chứng minh.

c. Ta có:

VT = (4 - √ 7)² = 4² – 2.4. √ 7 + (√ 7)² = 16 – 8√ 7 + 7 = 23 - 8√ 7

Vế trái bằng vế phải nên đẳng thức được chứng minh.

d. Ta có:

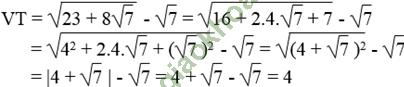
Vế trái bằng vế phải nên đẳng thức được chứng minh.

Bài 16 trang 7 Sách bài tập Toán 9 Tập 1: Biểu thức sau đây xác định với giá trị nào của x?

Bài giải:

Bài 17 trang 8 Sách bài tập Toán 9 Tập 1: Tìm x, biết:

Bài giải:

* Trường hợp 1: 3x ≥ 0 ⇔ x ≥ 0 ⇒ |3x| = 3x

=> 3x = 2x + 1 ⇔ 3x - 2x = 1 ⇔ x = 1

Giá trị x = 1 là nghiệm của phương trình (1).

* Trường hợp 2: 3x < 0 ⇔ x < 0 ⇒ |3x| = -3x

Suy ra: -3x = 2x + 1 ⇔ -3x - 2x = 1 ⇔ -5x = 1 ⇔ x = - 1/5

Giá trị x = - 1/5 thỏa mãn điều kiện x < 0

Vậy x = - 1/5 là nghiệm của phương trình (1).

Vậy x = 1 và x = - 1/5

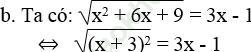
⇔ |x + 3| = 3x - 1 (2)

* Trường hợp 1: x + 3 ≥ 0 ⇔ x ≥ -3 ⇒ |x + 3| = x + 3

=> x + 3 = 3x - 1 ⇔ x - 3x = -1 - 3 ⇔ -2x = -4 ⇔ x = 2

Giá trị x = 2 thỏa mãn điều kiện x ≥ -3.

Vậy x = 2 là nghiệm của phương trình (2).

* Trường hợp 2: x + 3 < 0 ⇔ x < -3 ⇒ |x + 3| = -x - 3

=> -x - 3 = 3x - 1 ⇔ -x - 3x = -1 + 3 ⇔ -4x = 2 ⇔ x = -0.5

Giá trị x = -0,5 không thỏa mãn điều kiện x < -3: loại

Vậy x = 2

* Trường hơp 1: 1 - 2x ≥ 0 ⇔ 2x ≤ 1 ⇔ x ≤ 1/2 ⇒ |1 - 2x| = 1 - 2x

=> 1 - 2x = 5 ⇔ -2x = 5 - 1 ⇔ x = -2

Giá trị x = -2 thỏa mãn điều kiện x ≤ 1/2

Vậy x = -2 là nghiệm của phương trình (3).

* Trường hợp 2: 1 - 2x < 0 ⇔ 2x > 1 ⇔ x > 12 ⇒ |1 - 2x| = 2x - 1

=> 2x - 1 = 5 ⇔ 2x = 5 + 1 ⇔ x = 3

Giá trị x = 3 thỏa mãn điều kiện x > 1/2

Vậy x = 3 là nghiệm của phương trình (3).

Vậy x = -2 và x = 3.

⇔ |x²| = 7 ⇔ x² = 7

Vậy x = √ 7 và x = - √ 7.

Bài 18 trang 8 Sách bài tập Toán 9 Tập 1: Phân tích thành nhân tử:

a. x² - 7

b. x² - 2√ 2 x + 2

c. x² + 2√ 13 x + 13

Bài giải:

a. Ta có: x² - 7 = x² - (√ 7)² = (x + √ 7)(x - √ 7)

b. Ta có: x² - 2√ 2 x + 2 = x² - 2. x. √ 2 + (√ 2)² = (x - √ 2)²

c. Ta có: x² + 2√ 13 x + 13 = x² + 2. x. √ 13 + (√ 13)² = (x + √ 13)²

Bài 19 trang 8 Sách bài tập Toán 9 Tập 1: Rút gọn các phân thức:

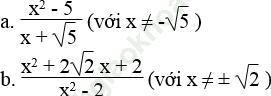
Bài giải:

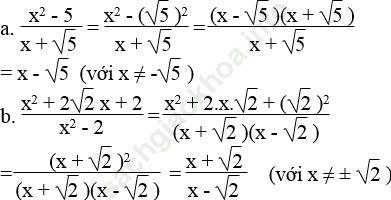
Bài 20 trang 8 Sách bài tập Toán 9 Tập 1: So sánh (không dùng bảng số hay máy tính bỏ túi):

a. 6+2√ 2 và 9

b. √ 2 + √ 3 và 3

c. 9 + 4√ 5 và 16

d. √ 11 - √ 3 và 2

Bài giải:

a. 6+2√ 2 và 9

Ta có: 9 = 6 + 3

So sánh: 2√ 2 và 3 vì 2√ 2 > 0 và 3 > 0

Ta có: (2√ 2)²=2². (√ 2)²=4.2=8

3²= 9

Vì 8 < 9 nên: (2√ 2)² < 3²

Vậy 6+2√ 2 < 9.

b. √ 2 + √ 3 và 3

Ta có: (√ 2 + √ 3)²= (√ 2)²+ 2. √ 2.√ 3 + (√ 3)² = 5 + 2. √ 2.√ 3

Mà 3²= 9= 5 + 2.2

Vì vậy chỉ cần so sánh √ 2.√ 3 và 2

Ta có: (√ 2)². (√ 3)²= 2.3 = 6

2²=4

Vì 6 > 4 nên (√ 2. √ 3)² > 2²

Suy ra: √ 2. √ 3 > 2 ⇒ 2. √ 2. √ 3 > 2.2 ⇒ 5 + 2. √ 2. √ 3 > 5 + 4

⇒ 5 + 2. √ 2. √ 3 > 9 ⇒ (√ 2 + √ 3)² > 9 ⇒ (√ 2 + √ 3)² > 3²

Vậy √ 2 + √ 3 > 3

c. 9 + 4√ 5 và 16

Ta có 16= 9 + 7

Vì vậy, ta sẽ đi so sánh 4√ 5 và 7

Ta có: (4√ 5)² = 16.5 = 80

7² = 49

Vì 80 > 49 => 4√ 5 > 7

Vậy: 9 + 4√ 5 > 16

d. √ 11 - √ 3 và 2

Vì √ 11 > √ 3 nên √ 11 - √ 3 > 0

Ta có: (√ 11 - √ 3)² = 11 - 2√ 11. √ 3 + 3 = 14 - 2√ 11. √ 3

2² = 4 = 14 – 10

Ta so sánh 10 và 2√ 11. √ 3 hay so sánh giữa 5 và √ 11. √ 3

Ta có: 5² = 25

(√ 11. √ 3)² = (√ 11)². (√ 3)² = 11.3 = 33

Vì 25 < 33 nên 5² < (√ 11. √ 3)²

Suy ra: 5 < (√ 11. √ 3)² hay 10 < 2√ 11. √ 3

Suy ra: 14 - 2√ 11. √ 3 < 14 - 10 ⇒ (√ 11 - √ 3)² < 2²

Vậy: √ 11 - √ 3 < 2

Bài 21 trang 8 Sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức:

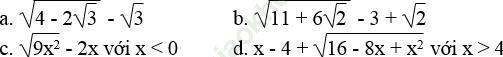
Bài giải:

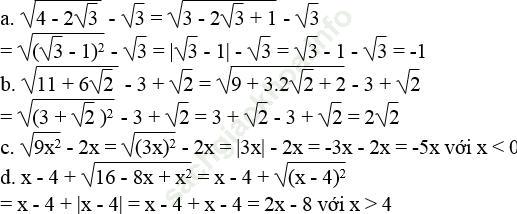
Bài 22 trang 8 Sách bài tập Toán 9 Tập 1: Với n là số tự nhiên, chứng minh đẳng thức:

Viết đẳng thức trên khi n là 1,2,3,4,5,6,7

Bài giải: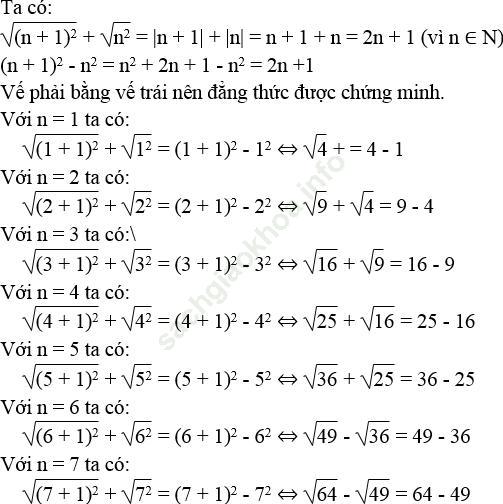

Bài tập bổ sung

Bài 2 trang 8 Sách bài tập Toán 9 Tập 1: Đẳng thức nào đúng nếu x là số âm:

A. √ (9x²) = 9x;

B. √ (9x²) = 3x;

C. √ (9x²) = -9x;

D. √ (9x²) = -3x.

Hãy chọn đáp án đúng.
Bài giải:

Đáp án đúng là: D

Bài trước: Bài 1: Căn bậc hai - trang 5 Sách bài tập Toán 9 Tập 1 Bài tiếp: Bài 3: Liên hệ giữa phép nhân và phép khai phương - trang 9 Sách bài tập Toán 9 Tập 1