Bài 3: Giải hệ phương trình bằng phương pháp thế - trang 9 Sách bài tập Toán 9 Tập 2

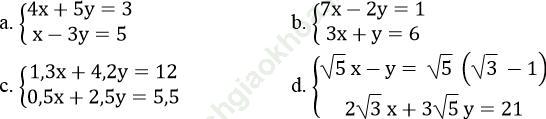
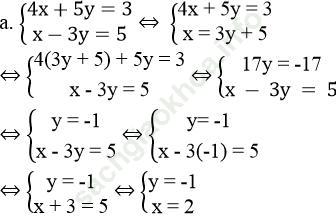
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (2; -1).

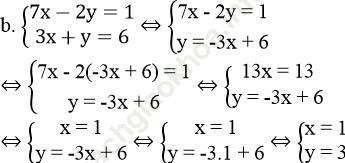
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (1; 3)

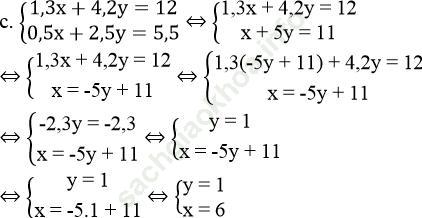
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (6; 1).

Bài 17 trang 9 Sách bài tập Toán 9 Tập 2: Giải các hệ phương trình:

Bài giải:

Vậy hệ phương trình có nghiệm duy nhất (x; y) = (148/127; - 52/127)

Vậy hệ phương trình có nghiệm duy nhất (x; y) = (0; 3 -√ 5).

Bài 18 trang 9 Sách bài tập Toán 9 Tập 2: Tìm giá trị của a và b:

a. Để hệ phương trình 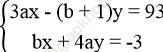có nghiệm là (x; y) = (1; -5)

b. Để hệ phương trình 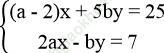có nghiệm là (x; y) = (3; -1)

Bài giải:

a. Thay x = 1, y = -5 vào hệ phương trình ta được:

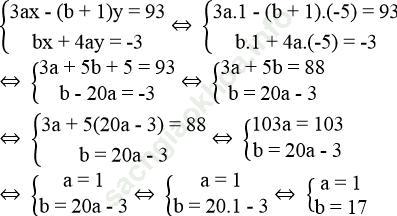
Vậy khi a = 1, b = 17 thì hệ phương trình 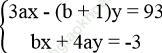có nghiệm là (x; y) = (1; -5).

b. Thay x = 3, y = -1 vào hệ phương trình ta được:

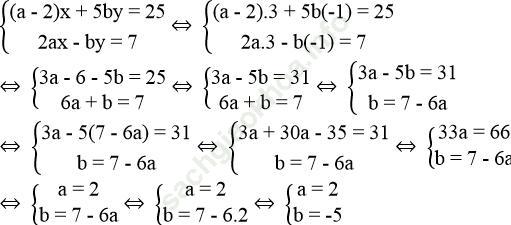
Vậy khi a = 2, b = -5 thì hệ phương trình 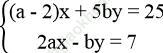có nghiệm là (x; y) = (3; -1).

Bài 19 trang 9 Sách bài tập Toán 9 Tập 2: Tìm giá trị của a và b để hai đường thẳng:

(d₁): (3a – 1)x + 2by = 56 và (d₂): cắt nhau tại điểm M (2; -5).

Bài giải:

Hai đường thẳng:

(d₁): (3a – 1)x + 2by = 56 và (d₂): cắt nhau tại điểm M (2; -5) nên tọa độ của M là nghiệm của hệ phương trình:

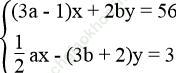
Thay x = 2, y = -5 vào hệ phương trình, ta có:

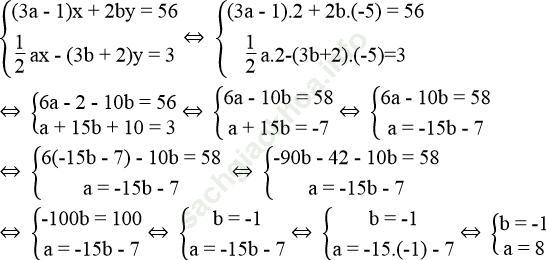
Vậy khi a = 8, b = -1 thì hai đường thẳng (d₁): (3a – 1)x + 2by = 56 và (d₂): cắt nhau tại điểm M (2; -5).

Bài 20 trang 9 Sách bài tập Toán 9 Tập 2: Tìm a và b để:

a. Đường thẳng y = ax + b đi qua hai điểm A (-5; 3), B (3/2; -1);

b. Đường thẳng ax – 8y = b đi qua điểm M (9; -6) và đi qua giao điểm của hai đường thẳng (d₁): 2x + 5y = 17, (d₂): 4x – 10y = 14.

Bài giải:

a. Đường thẳng y = ax + b đi qua hai điểm A (-5; 3), B (3/2; -1) nên tọa độ của A và B nghiệm đúng phương trình đường thẳng.

* Điểm A: 3 = -5a + b

*Điểm B:

Khi đó a và b là nghiệm của hệ phương trình:

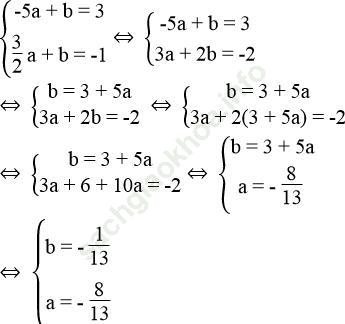
Vậy khi a = - 8/13; b = - 1/13 thì đường thẳng y = ax + b đi qua hai điểm A (-5; 3), B (3/2; -1).

Đường thẳng cần tìm là:

b. Tọa độ giao điểm của hai đường thẳng (d₁): 2x + 5y = 17, (d₂): 4x – 10y = 14 là nghiệm của hệ phương trình:

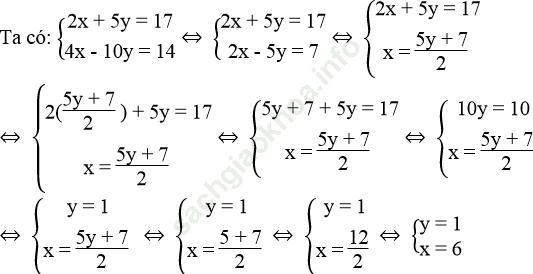
Khi đó (d₁) và (d₂) cắt nhau tại N (6; 1).

Đường thẳng ax – 8y = b đi qua điểm M (9; -6) và N (6; 1) nên tọa độ của M và N nghiệm đúng phương trình đường thẳng.

* Điểm M: 9a + 48 = b

* Điểm N: 6a – 8 = b

Khi đó a và b là nghiệm của hệ phương trình:

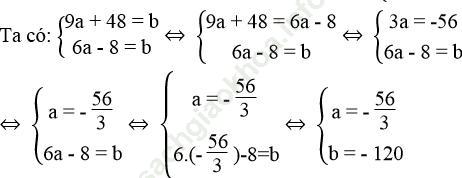
Vậy khi a = - 56/3, b = -120 thì đường thẳng ax – 8y = b đi qua điểm M (9; -6) và đi qua giao điểm của hai đường thẳng (d₁): 2x + 5y = 17, (d₂): 4x – 10y = 14.

Bài 21 trang 9 Sách bài tập Toán 9 Tập 2: Tìm giá trị của m để:

a. Hai đường thẳng (d₁): 5x – 2y = 3; (d₂): x + y = m cắt nhau tại một điểm trên trục Oy. Vẽ hai đường thẳng này trên cùng một mặt phẳng tọa độ.

b. Hai đường thẳng (d₁): mx + 3y = 10; (d₂): x – 2y = 4 cắt nhau tại một điểm trên trục Ox. Vẽ hai đường thẳng này trên cùng một mặt phẳng tọa độ.

Bài giải:

a. Giả sử hai đường thẳng (d₁): 5x – 2y = 3; (d₂): x + y = m cắt nhau tại điểm A (x, y).

Vì giao điểm A nằm trên trục Oy nên x = 0. Suy ra: A (0; y).

Khi đó điểm A (0; y) là nghiệm của hệ phương trình:

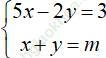
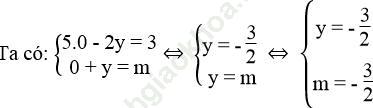
Vậy khi m = - 3/2 thì (d₁): 5x – 2y = 3; (d₂): x + y = m cắt nhau tại một điểm trên trục Oy.

Phương trình đường thẳng (d₂): x + y = - 3/2

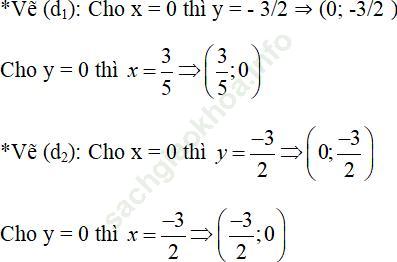
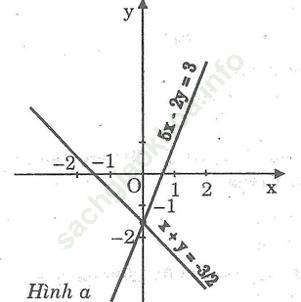
Đồ thị: hình a.

b. Giả sử hai đường thẳng (d₁): mx + 3y = 10; (d₂): x – 2y = 4 cắt nhau tại điểm B (x, y).

Vì điểm B nằm trên trục Ox nên y = 0 ⇒ B (x, 0).

Khi đó điểm B (x; 0) là nghiệm của hệ phương trình:

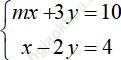
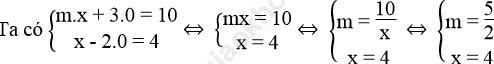
Vậy khi m = 5/2 thì (d₁): mx + 3y = 10; (d₂): x – 2y = 4 cắt nhau tại một điểm trên trục Ox.

Phương trình đường thẳng (d₁): 5x + 6y = 20

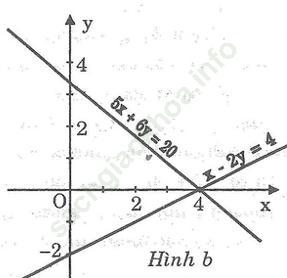
* Vẽ (d₁):

Cho x = 0 thì y = 10/3 ⇒ (0; 10/3)

Cho y = 0 thì x = 4 ⇒ (4; 0)

* Vẽ (d₂): x - 2y = 4.

Cho x = 0 thì y = -2 ⇒ (0; -2)

Cho y = 0 thì x = 4 ⇒ (4; 0)

Đồ thị: hình b.

Bài 22 trang 10 Sách bài tập Toán 9 Tập 2: Tìm giao điểm của hai đường thẳng:

a. (d₁): 5x – 2y = c và (d₂): x + by = 2, biết rằng (d₁) đi qua điểm A (5; -1) và (d₂) đi qua điểm B (-7; 3).

b. (d₁): ax + 2y = -3 và (d₂): 3x – by = 5, biết rằng (d₁) đi qua điểm M (3; 9) và (d₂) đi qua điểm N (-1; 2)

Bài giải:

a.

* Đường thẳng (d₁): 5x – 2y = c đi qua điểm A (5; -1) nên tọa độ điểm A nghiệm đúng phương trình đường thẳng.

Ta có: 5.5 – 2. (-1) = c ⇔ 25 + 2 = c ⇔ c = 27

Phương trình đường thẳng (d₁): 5x – 2y = 27

* Đường thẳng (d₂): x + by = 2 đi qua điểm B (-7; 3) nên tọa độ điểm B nghiệm đúng phương trình đường thẳng.

Ta có: -7 + 3b = 2 ⇔ 3b = 9 ⇔ b = 3

Phương trình đường thẳng (d₂): x + 3y = 2

* Tọa độ giao điểm của (d₁) và (d₂) là nghiệm của hệ phương trình:

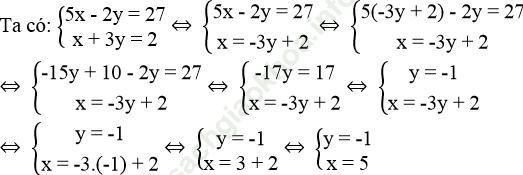
Vậy tọa độ giao điểm của (d₁) và (d₂) là (5; -1).

b.

* Đường thẳng (d₁): ax + 2y = -3 đi qua điểm M (3; 9) nên tọa độ điểm M nghiệm đúng phương trình đường thẳng.

Ta có: a. 3 + 2.9 = -3 ⇔ 3a + 18 = -3 ⇔ 3a = -21 ⇔ a = -7

Phương trình đường thẳng (d₁): -7x + 2y = -3

* Đường thẳng (d₂): 3x – by = 5 đi qua điểm N (-1; 2) nên tọa độ điểm N nghiệm đúng phương trình đường thẳng.

Ta có: 3. (-1) – b. 2 = 5 ⇔ -3 – 2b = 5 ⇔ 2b = -8 ⇔ b = -4

Phương trình đường thẳng (d₂): 3x + 4y = 5

* Tọa độ giao điểm của (d₁) và (d₂) là nghiệm của hệ phương trình:

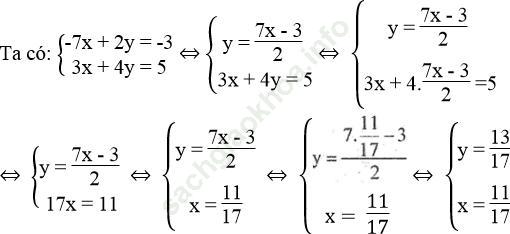
Bài 23 trang 10 Sách bài tập Toán 9 Tập 2: Giải các hệ phương trình:

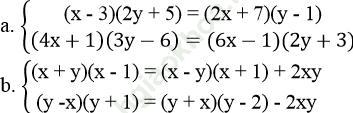
Bài giải:

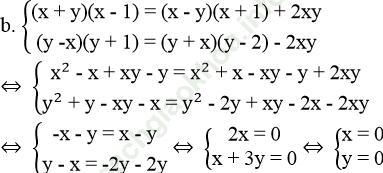
Vậy nghiệm của hệ phương trình là (x; y) = (0; 0)

Bài 24 trang 10 Sách bài tập Toán 9 Tập 2: Giải các hệ phương trình sau bằng cách đặt ẩn số phụ:

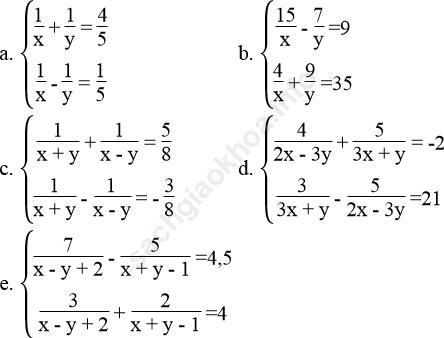
Bài giải:

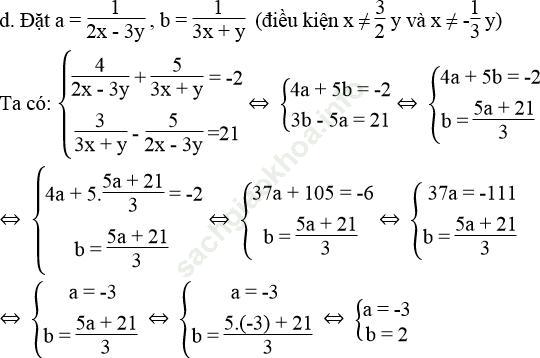
Vậy nghiệm của hệ phương trình là (x; y) = (1; 2).

Bài 1 trang 10 Sách bài tập Toán 9 Tập 2: Tìm a và b để hệ

Bài giải:

Cặp (x; y) = (1; -4) là nghiệm của hệ phương trình. Thay x = 1; y = -4 vào hệ phương trình ta có:

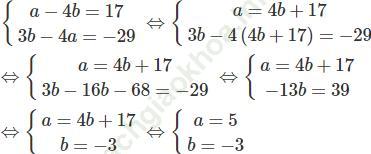
Vậy hằng số a = 5; b = -3

Bài 2 trang 10 Sách bài tập Toán 9 Tập 2: Giải hệ phương trình:

Bài giải:

Ta đưa về giải hai hệ phương trình:

hoặc

Giải hệ:

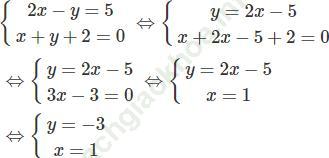
Giải hệ:

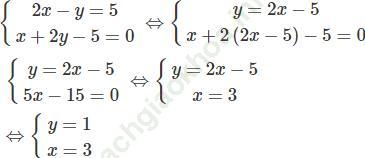
Vậy hệ phương trình đã cho có hai nghiệm

(x₁; y₁) = (1; -3) và (x₂; y₂) = (3; 1)