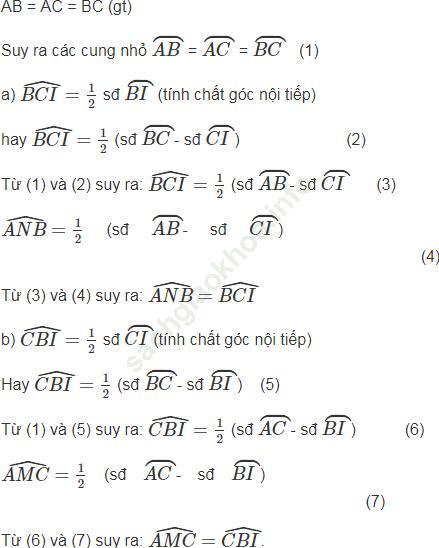Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn - trang 105 Sách bài tập Toán 9 Tập 2
Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn
Bài 28 trang 105 Sách bài tập Toán 9 Tập 2: Các điểm A1,A2,A3,…. A19,A20 được sắp xếp theo thứ tự đó trên đường tròn (O) và chia đường tròn thành 20 cung bằng nhau. Chứng minh rằng dây A1A8 vuông góc với dây A3A16
Bài giải:Gọi giao điểm của A1A8 và A3A16 là M
Vì đường tròn được chia thành 20 cung
bằng nhau nên số đo của mỗi cung là:
360°: 20 = 180°

Bài 29 trang 105 Sách bài tập Toán 9 Tập 2: Cho tam giác ABC vuông ở A. Đường tròn đường kính AB cắt BC ở D. Tiếp tuyến ở D cắt AC ở P. Chứng minh rằng PD = PC

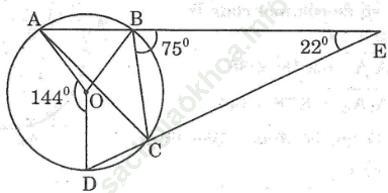
Bài 30 trang 105 Sách bài tập Toán 9 Tập 2: Hai dây cung AB và CD kéo dài cắt nhau tại điểm E ở ngoài đường tròn (O) (C nằm giữa A và E, C nằm giữa D và E).
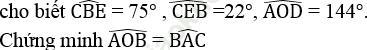
Bài giải:

Bài 31 trang 105 Sách bài tập Toán 9 Tập 2: A, B, C là ba điểm thuộc đường tròn (O) sao cho tiếp tuyến tại A cắt tia BC tại D. Tia phân giác của góc (BAC) cắt đường tròn ở M, tia phân giác của góc D cắt AM ở I. Chứng minh DI ⊥ AM.
Bài giải: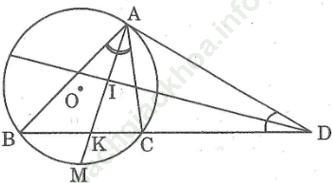

Suy ra tam giác AKD cân tại D
Tam giác AKD cân tại D có DI là tia phân giác nên DI cũng là đường cao
Suy ra: DI ⊥ AN hay DI ⊥ AM
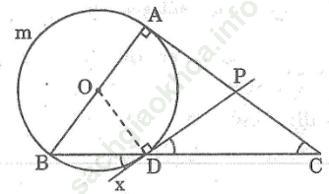
Bài 32 trang 105 Sách bài tập Toán 9 Tập 2: Trên đường tròn (O; R) vẽ ba dây liên tiếp bằng nhau AB, BC, CD mỗi dây có độ dài nhỏ hơn R. Các đường thẳng AB, CD cắt nhau tại I các tiếp tuyến của đường tròn tại B, D cắt nhau tại K
Bài giải:
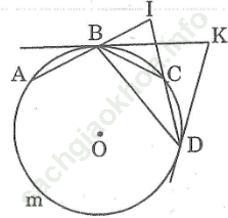

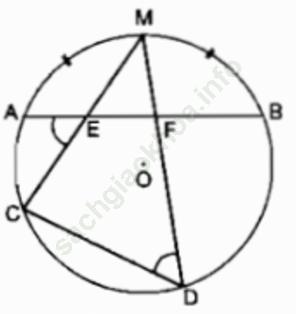
Bài 1 trang 105 Sách bài tập Toán 9 Tập 2: Cho đường tròn tâm O bán kính R và dây AB bất kỳ. Gọi M là điểm chính giữa của cung nhỏ AB. E và F là hai điểm bất kỳ trên dây AB. Gọi C và D tương ứng là giao điểm của ME, MF của đường tròn (O)
Bài giải:

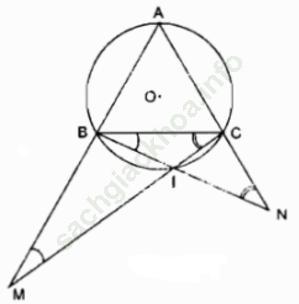
Bài 2 trang 105 Sách bài tập Toán 9 Tập 2: Cho đường tròn tâm O bán kính R. Lấy 3 điểm A, B, C trên đường tròn đó sao cho
AB = BC = CA. Gọi I là điểm bất kỳ của cung nhỏ BC (và I không trùng với B, C).
Gọi M là giao điểm của CI và AB. Gọi N là giao điểm của BI và AC. Chứng minh:
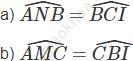
Bài giải: