Bài 7: Tứ giác nội tiếp - trang 106 Sách bài tập Toán 9 Tập 2
Bài 7: Tứ giác nội tiếp
Bài 39 trang 106 Sách bài tập Toán 9 Tập 2: Trên đường tâm O có một cung AB và S là điểm chính giữa của cung đó. Trên dây AB lấy hai điểm E và H. Các đường thẳng SH và SE cắt đường tròn theo thứ tự tại C và D. Chứng minh EHCD là một tứ giác nội tiếp
Bài giải: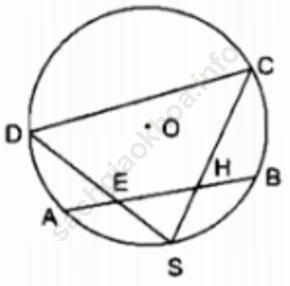
Bài 40 trang 106 Sách bài tập Toán 9 Tập 2: Cho tam giác ABC. Các đường phân giác trong của góc B và góc C cắt nhau tại S, các đường phân giác ngoài của góc B và góc C cắt nhau tại E. Chứng minh BSCE là một tứ giác nội tiếp
Bài giải: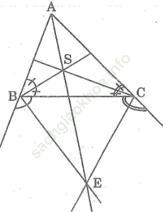
Ta có: BS ⊥ BE (tính chất đường phân giác của hai góc kề bù)
Và CS ⊥ CE (tính chất đường phân giác của hai góc kề bù)
Xét tứ giác BSCE ta có:
Vậy tứ giác BDCE nội tiếp tròn cung đường tròn
Bài 41 trang 106 Sách bài tập Toán 9 Tập 2: Cho tam giác ABC có đáy BC và góc A = 20°. Trên nửa mặt phẳng bờ AB không chứa điểm C lấy điểm D sao cho DA = DB và góc (DAB) =40°. Gọi E là giao điểm của AB và CD
a. Chứng minh ACBD là một tứ giác nội tiếp
b. Tính góc (AED)
Bài giải: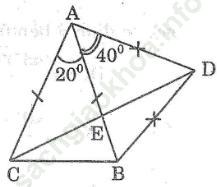


Bài 42 trang 107 Sách bài tập Toán 9 Tập 2: Cho ba đường tròn ùng đi qua một điểm P. Gọi các giao điểm khác P của hai trong ba đường tròn đó là A, B, C. Từ một điểm D (khác điểm P) trên đường tròn (PBC) kẻ các tia DB, DC cắt các đường tròn (PAB), (PAC) lần lượt tại M, N. Chứng minh ba điểm M, A, N thẳng hàng
Bài giải: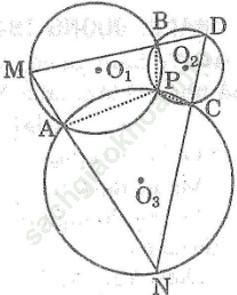
Gọi O1, O2, O3 lần lượt là tâm của ba đường tròn
Ta có: (O1) cắt (O2) tại A, (O2) cắt (O3) tại C, (O3) cắt (O1) tại B
Suy ra: D là điểm nằm trên (O3)
DB cắt (O1) tại M, DC cắt (O2) tại N
Nối MA, NA, PA, PB, PC
*Tứ giác APBM nội tiếp trong đường tròn (O1) nên ta có:

Bài 43 trang 107 Sách bài tập Toán 9 Tập 2: Cho đoạn thẳng AC và BD cắt nhau tại E
Biết AE. EC=BE. ED. Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn
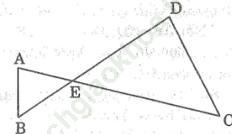
Bài giải:
Ta có: AE. EC=BE. ED (gt)
Suy ra: AE/ED = BE/EC
Xét Δ ABE và Δ DCE ta có:
AE/ED = BE/EC

Vì A và D nhìn đoạn BC cố định dưới một góc bằng nhau nên A và D nằm trên một cung chứa góc vẽ trên BC hay bốn điểm A, B, C, D cùng nẳm trên một đường tròn
Bài 1 trang 107 Sách bài tập Toán 9 Tập 2: Cho tam giác ABC có ba góc nhọn. Vẽ các đường cao AI, BK, CL của tam giác ấy.
Gọi H là giao điểm của các đường cao vừa vẽ.
a) Chỉ ra các tứ giác nội tiếp có đỉnh lấy trong số các điểm A, B, C, H, I, K, L
b) Chứng minh
c) Chứng minh KB là tia phân giác của
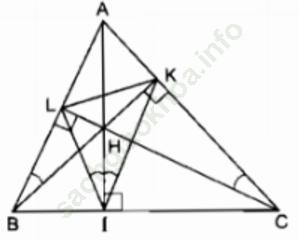
Vì ∆ABC là tam giác nhọn nên ba đường cao cắt nhau tại điểm H nằm trong tam giác ABC.
a) Tứ giác AKHL có
Tứ giác AKHL nội tiếp.
Tứ giác BIHL có
Tứ giác BIHL nội tiếp.
Tứ giác CIHK có
Tứ giác CIHK nội tiếp.
Tứ giác ABIK có
K và I nhìn đoạn AB dưới một góc vuông nên tứ giác ABIK nội tiếp. Tứ giác BCKL có
K và L nhìn đoạn BC dưới một góc vuông nên tứ giác BCKL nội tiếp.
Tứ giác ACIL có
I và L nhìn đoạn AC dưới một góc vuông nên tứ giác ACIL nội tiếp.
b) Tứ giác BIHL nội tiếp.
Tứ giác CIHK nội tiếp.
Tứ giác BCKL nội tiếp.
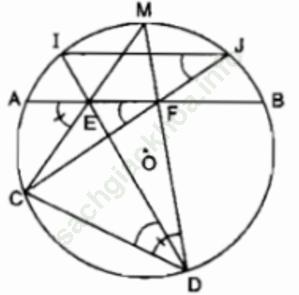
Bài 2 trang 107 Sách bài tập Toán 9 Tập 2: Cho đường tròn tâm O bán kính R và hai dây AB, CD bất kì. Gọi M là điểm chính giữa của cung nhỏ AB. Gọi E và F tương ứng là giao điểm của MC, MD với dây AB. Gọi I và J tương ứng là giao điểm của DE, CF với đường tròn (O). Chứng minh IJ song song với AB.