Bài 7: Vị trí tương đối của hai đường tròn - trang 167 Sách bài tập Toán 9 Tập 1
Bài 7: Vị trí tương đối của hai đường tròn
Bài 64 trang 167 Sách bài tập Toán 9 Tập 1: Cho hình bên, trong đó hai đường tròn (O) và (O’) tiếp xúc với nhau tại A. Chứng minh rằng các tiếp tuyến Bx và Cy song song với nhau.
Bài giải: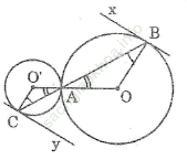
Ta có: O, A, O’ thẳng hàng
C, A, B thẳng hàng
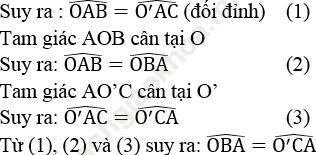
Suy ra OB // O’C (vì có cặp góc so le trong bằng nhau)
Lại có: Bx ⊥ OB (tính chất tiếp tuyến)
Suy ra: Bx ⊥ O’C
Mà: Cy ⊥ O’C (tính chất tiếp tuyến)
Suy ra: Bx // Cy
Bài 65 trang 167 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B như hình bên.
Biết OA = 15cm, O’A = 13cm, AB = 24cm. Tính độ dài OO’.
Bài giải: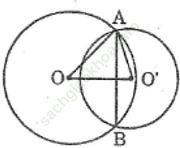
Gọi H là giao điểm của AB và OO’.
Vì OO’ là đường trung trực của AB nên:
OO’ ⊥ AB tại H
Suy ra: HA = HB = (1/2).AB = (1/2).24 = 12 (cm)
Áp dụng định lí Pitago vào tam giác vuông AOH, ta có:
AO2 = OH2 + AH2
Suy ra: OH2 = OA2 – AH2 = 152 – 122 = 81
OH = 9 (cm)
Áp dụng định lí pitago vào tam giác vuông AO’H, ta có:
AO’2 = O’H2 + AH2
Suy ra: O’H2= O’A2– AH2 = 132 – 122 = 25
O’H = 5 (cm)
Vậy OO’ = OH + O’H = 9 + 5 = 14 (cm)
Bài 66 trang 167 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc với nhau tại A như hình bên. Chứng minh rằng các bán kính OB và O’C song song với nhau.
Bài giải:
Ta có: OA = OB (= R)
Suy ra tam giác AOB cân tại O
Suy ra: OB // O’C (vì có hai góc ở vị trí đồng vị bằng nhau)
Bài 67 trang 167 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Kẻ các đường kính AOC, AO’D. Chứng minh rằng ba điểm C, B, D thẳng hàng và AB ⊥ CD
Bài giải: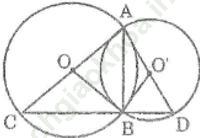
Tam giác ABC nội tiếp trong đường tròn (O) có AC là đường kính nên góc (ABC) = 90o
Tam giác ABD nội tiếp trong đường tròn (O’) có AD là đường kính nên góc (ABD) = 90o
Ta có:
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD
Bài 68 trang 168 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Gọi I là trung điểm của OO’. Qua A vẽ đường thẳng vuông góc với IA, cắt các đường tròn (O) và (O’) tại C và D (khác A). Chứng minh rằng AC = AD
Bài giải: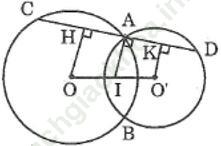
Kẻ OH ⊥ CD, O’K ⊥ CD
Ta có: IA ⊥ CD
Suy ra: OH // IA // O’K
Theo giả thiết: IO = IO’
Suy ra: AH = AK (tính chất đường thẳng song song cách đều) (1)
Ta có: OH ⊥ AC
Suy ra: HA = HC = (1/2).AC (đường kính dây cung) ⇒ AC = 2AH (2)
Lại có: O’K ⊥ AD
Suy ra: KA = KD = (1/2).AD (đường kính dây cung) ⇒ AD = 2AK (3)
Từ (1), (2) và (3) suy ra: AC = AD
Bài 69 trang 168 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B, trong đó O’ nằm trên đường tròn (O). Kẻ đường kính O’OC của đường tròn (O).
a. Chứng minh rằng CA, CB là các tiếp tuyến của đường tròn (o’)
b. Đường vuông góc với AO’ tại O’ cắt CB ở I. Đường vuông góc với AC tại C cắt đường thẳng O’B ở K. Chứng minh rằng ba điểm O, I, K thẳng hàng.
Bài giải: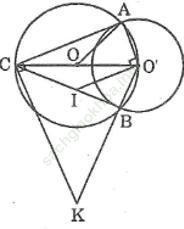
a. Tam giác AO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên
Suy ra: CA ⊥ O’A tại điểm A
Vậy CA là tiếp tuyến của đường tròn (O’)
Tam giác BO’C nội tiếp trong đường tròn (O) có O’C là đường kính nên
Suy ra: CB ⊥ O’B tại điểm B
Vậy CB là tiếp tuyến của đường tròn (O’)
b. Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C
Suy ra: 
(tính chất hai tiếp tuyến cắt nhau)
Mà O’I ⊥ O’A (gt)
CA ⊥ O’A (chứng minh trên)
Suy ra: O’I // CA => 
(hai góc so le trong)
Suy ra: 
Hay tam giác CIO’ cân tại I => IC = IO’
Khi đó I nằm trên đường trung trực của O’C
Lại có: 
(tính chất hai tiếp tuyến cắt nhau)
KC ⊥ CA (gt)
O’A ⊥ AC (chứng minh trên)
Suy ra: KC // O’A => 
(hai góc so le trong)
Suy ra: 
Hay tam giác CKO’ cân tại K => KC = KO’
Khi đó K nằm trên đường trung trực của O’C
Mặt khác: OC = OO’ (= R)
Suy ra O, I, K nằm trên đường trung trực của O’C
Vậy O, I, K thẳng hàng.
Bài 70 trang 168 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Dây AC của đường tròn (O) tiếp xúc với đường tròn (O’) tại A. Dây AD của đường trong (O’) tiếp xúc với đường tròn (O) tại A. Gọi K là điểm đối xứng với A qua trung điểm I của OO’, E là điểm đối xứng với A qua B. Chứng minh rằng:
a. AB ⊥ KB
b. Bốn điểm A, C, E, D cùng nằm trên một đường tròn
Bài giải: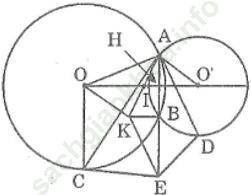
a. Gọi H là giao điểm của AB và OO’
Vì OO’ là đường trung trực của AB nên OO’ ⊥ AB tại H
Ta có: HA = HB
I là trung điểm của OO’ nên IH ⊥ AB (1)
Trong tam giác ABK, ta có:
HA = HB (chứng minh trên)
IA = IK (tính chất đối xứng tâm)
Suy ra IH là đường trung bình của tam giác ABK
Suy ra IH // BK (2)
Từ (1) và (2) suy ra: AB ⊥ KB
b. Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE (tính chất đối xứng tâm)
Suy ra: KA = KE (tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK (chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))
OK // O’A (chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC (tính chất đường trung trực) (4)
DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))
O’K // OA (chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD (tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn. 3
Bài 1 trang 168 Sách bài tập Toán 9 Tập 1: Cho h. bs. 23, trong đó OA = 3, O’A = 2, AB = 5. Độ dài AC bằng?
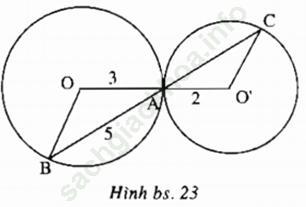
A. 10/3;
B. 3,5;
C. 3;
D. 4.
Hãy chọn phương án đúng.
Bài giải:Đáp án đúng là: A. 10/3
Bài 2 trang 168 Sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Một đường thẳng vuông góc với AB tại B cắt đường tròn (O) và (O’) theo thứ tự C và D (khác B). Chứng minh rằng OO’ = 1/2CD.
Bài giải: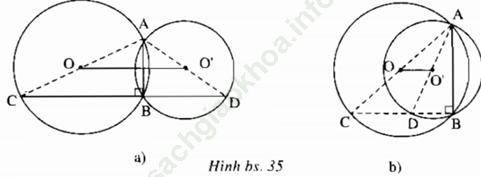
∠ (ABC) = 90o nên A, O, C thẳng hàng.
∠ (ABD) = 90o nên A, O’, D thẳng hàng.
OO’ là đường trung bình của tam giác Δ ACD nên OO’ = 1/2CD (đpcm)
Bài trước: Bài 6: Tính chất của hai tiếp tuyến cắt nhau - trang 164 Sách bài tập Toán 9 Tập 1 Bài tiếp: Bài 8: Vị trí tương đối của hai đường tròn (tiếp theo) - trang 168 Sách bài tập Toán 9 Tập 1