Bài 10: Diện tích hình tròn, hình quạt tròn - trang 111 Sách bài tập Toán 9 Tập 2
Bài 10: Diện tích hình tròn, hình quạt tròn
Bài 63 trang 111 Sách bài tập Toán 9 Tập 2:
a. Điền vào ô trống trong bảng sau (S là diện tích hình tròn có bán kính R)
| R | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 20 |
| S |
b. Vẽ đồ thị biểu diễn diện tích hình tròn theo bán kính của nó
c. Diện tích hình tròn có tỉ lệ thuận với bán kính không?
Bài giải:a.
| R | 0 | 1 | 2 | 3 | 4 | 5 | 10 | 20 |
| S | 0 | π | 4π | 9π | 16π | 25π | 100π | 400π |
b. Vẽ đồ thị
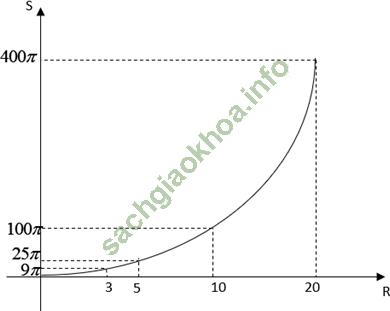
c. Diện tích hình tròn không tỉ lệ thuận với bán kính.
Bài 64 trang 111 Sách bài tập Toán 9 Tập 2:
a. Điền vào ô trống trong bảng sau (S là diện tích hình quạt no)
| Cung no | 0 | 45 | 90 | 180 | 360 |
| S |
b. Vẽ đồ thị diện tích hình quạt theo no
c. Diện tích hình quạt có tỉ lệ thuận với số đo độ của cung không?
Bài giải:a. Hoàn thành bảng như sau:
| Cung no | 0 | 45 | 90 | 180 | 360 |
| S | 0 | (πR2)/8 | (πR2)/4 | (πR2)/2 | πR2 |
b. Đồ thị diện tích hình quạt theo no
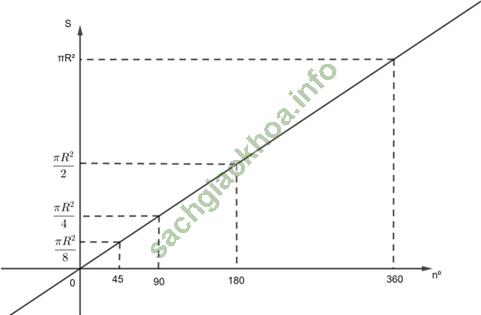
c. Diện tích hình quạt tỉ lệ thuận với số đo độ của cung.
Bài 65 trang 112 Sách bài tập Toán 9 Tập 2: Tính diện tích hình tròn biết chu vi của nó là C
Bài giải:Gọi R và S lần lượt là bán kính và diện tích của hình tròn
Ta có: C = 2πR ⇒ R = C2π
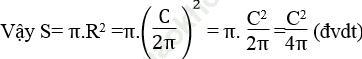
Bài 66 trang 112 Sách bài tập Toán 9 Tập 2: So sánh diện tích phần tô màu và phần để trắng trong hình sau:
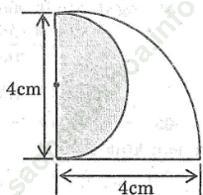
Phần tô màu là nửa hình tròn có đường kính 4cm nên bán kính bằng 2cm
Diện tích phần tô màu:
Diện tích phần tô màu và diện tích phần đẻ trắng = 1/4 hình tròn có bán kính 4cm
Như vậy, diện tích phần để trắng: S2 = S - S1 = 4 π - 2 π =2 π (cm2)
Vậy diện tích hai phần bằng nhau.
Bài 67 trang 112 Sách bài tập Toán 9 Tập 2:
a. Vẽ đường xoắn (hình sau) xuất phát từ một hình vuông cạnh 1cm. Nêu cách vẽ
b. Tính diện tích phần tô màu.
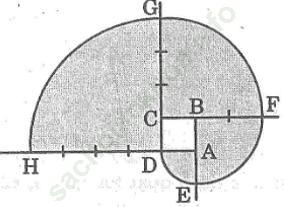
a. Cách vẽ:
-Vẽ 1/4 đường tròn tâm A bán kính 1cm ta được cung DE
- Vẽ 1/4 đường tròn tâm B bán kính 2cm ta được cung EF
- Vẽ 1/4 đường tròn tâm C bán kính 3cm ta được cung FG
- Vẽ 1/4 đường tròn tâm D bán kính 4cm ta được cung GH
b. Tính S phần tô màu như sau:
Ta có:
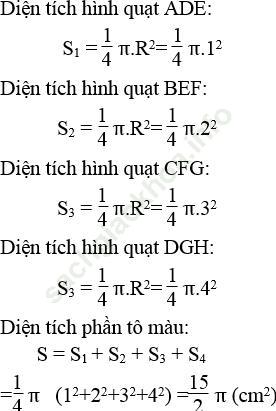
Bài 68 trang 112 Sách bài tập Toán 9 Tập 2: Một chiếc bàn hình tròn được ghép bởi hai hình tròn đường kính 1,2 cm. Người ta muốn nới rộng mặt bàn bằng cách ghép thêm (vào giữa) một mặt hình chữ nhật có một kích thước là 1,2cm (hình dưới)
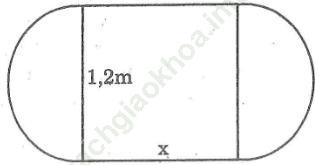
a. Kích thước kia của hình chữ nhật phải là bao nhiêu nếu diện tích mặt bàn tăng gấp đôi sau khi nới?
b. Kích thước kia của hình chữ nhật phải là bao nhiêu nếu chu vi mặt bàn tăng gấp đôi sau khi nới?
Bài giải:a. Goi x (m) là kích thước còn lại của hình chữ nhật
Điều kiện: x > 0
Ta có: 1,2x + π (0,6)2 = 2π (0,6)2
⇔ 1,2x = 2π (0,6)2 - π (0,6)2 = π 0,36
⇔ x = (0.36. π)/ (1.2) = 0,942cm
Vậy kích thước còn lại của hình chữ nhật phải là 0,942m
b. Chu vi mặt bàn sau khi tăng gấp đôi: 2.1,2π = 2,4π (m)
Theo đề bài, ta có: 1,2π + 2.1,2x = 2,4π
⇔ 2,4x =2,4π -1,2π = 1,2π
⇔ x= (1.2π)/ (2.4) =π 0.5=1,57m
Vậy kích thước còn lại của hình chữ nhật phải là 1,57m
Bài 69 trang 112 Sách bài tập Toán 9 Tập 2: Cho đường tròn (O; R) chia đường tròn này thành ba cung có số đo tỉ lệ với 3,4,5. Tính diện tích các hình quạt tròn được tạo thành
Bài giải:Gọi x, y, z lần lượt là số đo độ của ba cung. Ta có: x+y+z=360°
Theo đề bài ta có: x/3 =y/4 =z/5 = (x+y+z)/ (3+4+5) =360° /12 = 30°
Suy ra: x= 3.30° =90°; y = 4.30° = 120°; z = 5.30° = 150°
Diện tích hình quạt tương ứng với các cung 90°, 120°, 150° là:
Bài 70 trang 112 Sách bài tập Toán 9 Tập 2: Cho tam giác ABC nội tiếp trong đường tròn (O; R) có góc C =45°
a. Tính diện tích hình quạt tròn AOB (ứng với cung nhỏ AB)
b. Tính diện tích hình viên phân AmB (ứng với cung nhỏ AB)
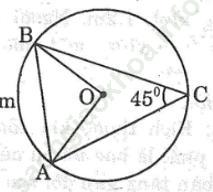
Bài giải:

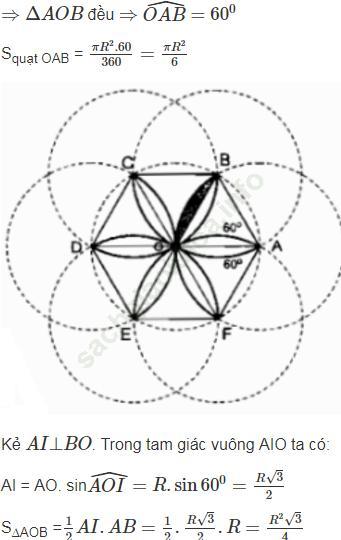
Bài 71 trang 113 Sách bài tập Toán 9 Tập 2: Trong tam giác đều ABC, vẽ những cung tròn đi qua tâm của tam giác và từng cặp đỉnh của nó. Cho biết cạnh tam giác bằng a, tính diện tích hình hoa thị gạch sọc.
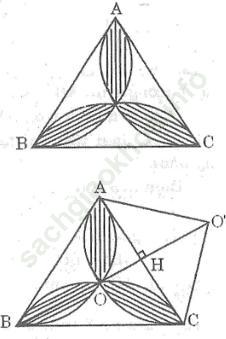
Gọi O là tâm của tam giác đều ABC
Ta có: OA =OB=OC
Vì ABC là tam giác đều nên AO, BO, CO là tia phân giác của góc A, góc B, góc C trong Δ OAC ta có:


Bài 72 trang 113 Sách bài tập Toán 9 Tập 2: Cho tam giác ABC vuông ở A và đường cao AH. Vẽ đường tròn tam O đường kính AB. Biết BH = 2cm và HC = 6cm. Tính:
a. Diện tích hình tròn (O)
b. Tổng diện tích hai hình viên phân AmH và BnH (ứng với các cung nhỏ)
c. Diện tích hình quạt tròn AOH (ứng với các cung nhỏ AH)
Bài giải: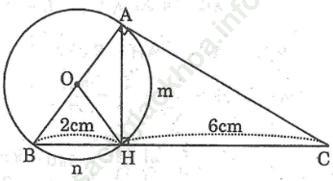
a) Trong tam giác ABC vuông tại A nên ta có:
AB2 = BH. BC =2. (2+6)=2.8=16
suy ra AB = 4cm
Diện tích hình tròn tâm (O) là:
S=π. (AB/2)2= π. (4/2)2 = 4π (cm2)
b) Trong tam giác vuông ABC có:
AH2 = HB. HC =2.6=12
Suy ra: AH =2. √ 3 cm
Diện tích tam giác AHB:
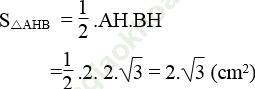
Tổng diện tích hai hình viên phân AmH và BnH bằng diện tích nửa hình tròn tâm O trừ diện tích tam giác AHB co:
S = 2π - 2. √ 3 = 2 (π - √ 3) (cm2)
c) Ta có AB=4cm ⇒ OB =2cm
Tam giác OBH có OB = OH =HB = 2cm nên tam giác OBH đều
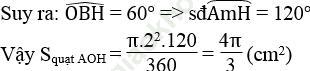
Bài 1 trang 113 Sách bài tập Toán 9 Tập 2: Tính diện tích của hình được giới hạn bởi các đường cong, biết OA = OB = R > 0 (h. bs. 7).
Bài giải:
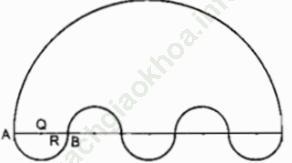
Hình đó gồm nửa hình tròn bán kính 5R, 3 nửa hình tròn bán kính R và bớt đi 2 nửa hình tròn bán kính R.
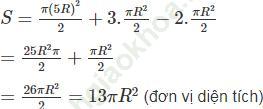
Bài 2 trang 113 Sách bài tập Toán 9 Tập 2: Tính diện tích của hình cánh hoa, biết OA = R (h. bs. 8).
Bài giải:
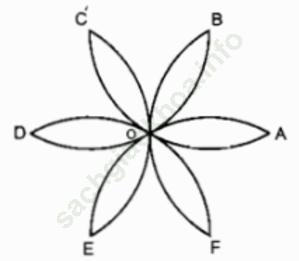
Ta có 12 hình viên phân có diện tích bằng nhau tạo nên cánh hoa đó.
Xét hình viên phân giới hạn bởi cung BO và dây căng cung đó thì cung BO là cung của đường tròn tâm A bán kính R.
OA = AB = OB = R