Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn - trang 156 Sách bài tập Toán 9 Tập 1
Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Bài 1 trang 156 Sách bài tập Toán 9 Tập 1: Cho hình chữ nhật ABCD có AD = 12cm, CD = 16cm. Chứng minh rằng bốn điểm ABCD cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
Bài giải: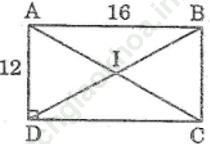
Gọi I là giao điểm của hai đường chéo AC và BD. Ta có:
IA = IB = IC = ID (tính chất hình chữ nhật)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn bán kính AC/2
Áp dụng định lí Pitago vào tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = 162 + 122 = 256 + 144 = 400
Suy ra: AC = √ 400 = 20 (cm)
Vậy bán kính đường tròn là: IA = AC/2 = 20/2 = 10 (cm)
Bài 2 trang 156 Sách bài tập Toán 9 Tập 1: Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí tương đối của mỗi điểm A (1; -1), B (-√ 2; √ 2) và C (1; 2) đối với đường tròn (O; 2)
Bài giải:Gọi R là bán kính của đường tròn (O; 2). Ta có: R = 2
OA2 = 12 + 12 = 2 ⇒ OA = √ 2 < 2
Vì OA < R nên điểm A nằm trong đường tròn (O; 2)
OB2 = (√ 2)2 + (√ 2)2 = 2 + 2 = 4 ⇒ OB = 2
Vì OB = R nên điểm B thuộc đường tròn (O; 2)
OC2 = 12 + 22 = 1 + 4 = 5 ⇒ OC = √ 5 > 2
Bài 3 trang 156 Sách bài tập Toán 9 Tập 1: Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được khẳng định đúng:
| (1) Tập hợp các điểm có khoảng cách đến điểm O cố định bằng 3cm | (4) có khoảng cách đến điểm O nhỏ hơn hoặc bằng 3cm. |
| (2) Đường tròn tâm O bán kính 3cm gồm tất cả những điểm | (5) cách điểm O một khoảng bằng 3cm |
| (3) Hình tròn tâm O bán kính 3cm gồm tất cả những điểm | (6) là đường tròn tâm O bán kính 3cm |
| (7) có khoảng cách đến điểm O lớn hơn 3cm |
Bài giải:
(1) - (6)
(2) - (5)
(3) - (4)
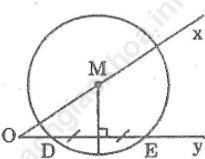
Bài 4 trang 156 Sách bài tập Toán 9 Tập 1: Cho góc nhọn xOy và hai điểm D, E thuộc tia Oy. Dựng đường tròn tâm M đi qua D và E sao cho tâm M nằm trên tia Ox.
Bài giải:* Cách dựng:
- Dựng đường trung trực của DE cắt Ax tại M
- Dựng đường tròn tâm M bán kính MD
* Chứng minh:
Theo cách dựng ta có: M ∈ Ox
MD = ME (tính chất đường trung trực)
Suy ra: E ∈ (M; MD).
Bài 5 trang 156 Sách bài tập Toán 9 Tập 1: Trong các câu sau, câu nào đúng, câu nào sai?
a. Hai đường tròn phân biệt có thể có hai điểm chung
b. Hai đường tròn phân biệt có thể có ba điểm chung phân biệt
c. Tâm của đường tròn ngoại tiếp một tam giác bao giờ cũng nằm trong tam giác ấy.
Bài giải:a. Đúng
b. Sai vì hai đường tròn có ba điểm chung phân biệt thì chúng trùng nhau
c. Sai vì tam giác vuông có tâm đường tròn ngoại tiếp nằm trên cạnh huyền, tam giác tù giao điểm của ba đường trung trực nằm ngoài tam giác.
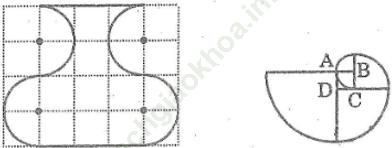
Bài 6 trang 157 Sách bài tập Toán 9 Tập 1:
a. Quan sát hình lọ hoa trên giấy kẻ ô vuông (hình dưới) rồi vẽ lại hình đó vào vở
b. Quan sát đường tròn xoắn ốc (hình dưới) rồi vẽ lại hình đó vào vở. Tính bán kính của các cung tròn tâm B, C, D, A biết cạnh hình vuông ABCD bằng 1 đơn vị dài.
Bài giải:
a. Hình a
b. Hình b
Cung tròn tâm B có bán kính bằng 1.
Cung tròn tâm C có bán kính bằng 2.
Cung tròn tâm D có bán kính bằng 3.
Cung tròn tâm A có bán kính bằng 4.
Bài 7 trang 157 Sách bài tập Toán 9 Tập 1: Hình bên. Có một chi tiết máy (mà đường viền ngoài là đường tròn) bị gãy. Làm thế nào để xác định được bán kính của đường viền?

Bài giải:
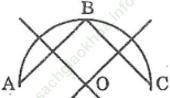
Lấy ba điểm A, B, C phân biệt trên đường viền.
Dựng đường trung trực của AB và BC. Hai đường trung trực cắt nhau tại O.
OA, OB, OC chính là bán kính của đường viền.
Bài 8 trang 157 Sách bài tập Toán 9 Tập 1: Cho hình vuông ABCD, O là giao điểm của hai đường chéo, OA = √ 2 cm. Vẽ đường tròn tâm A bán kính 2cm. Trong năm điểm A, B, C, D, O, điểm nào nằm trên đường tròn? Điểm nào nằm trong đường tròn? Điểm nào nằm ngoài đường tròn?
Bài giải: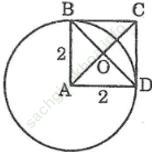
OA = √ 2 < 2 nên điểm O và A nằm trong (A; 2)
AB = 2 nên điểm B nằm trên (A; 2)
AD = 2 nên điểm D nằm trên (A; 2)
AC = 2√ 2 > 2 nên điểm C nằm ngoài (A; 2)
Bài 9 trang 157 Sách bài tập Toán 9 Tập 1: Cho tam giác nhọn ABC. Vẽ đường tròn (O) có đường kính BC, nó cắt các cạnh AB, AC theo thứ tự ở D, E
a. Chứng minh rằng CD ⊥ AB, BE ⊥ AC
b. Gọi K là giao điểm của BE và CD. Chứng minh rằng AK vuông góc với BC.
Bài giải:a. Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại D.
Suy ra: CD ⊥ AB.
Tam giác BCE nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại E.
Suy ra: BE ⊥ AC.
b. K là giao điểm của hai đường cao CD và BE nên K là trực tâm của tam giác ABC
Suy ra: AK ⊥ BC
Bài 10 trang 157 Sách bài tập Toán 9 Tập 1: Cho tam giác đều ABC cạnh bằng 3cm. Bán kính của đường tròn ngoại tiếp tam giác ABC bằng:
A. 2√ 3 cm
B. 2cm
C. √ 3 cm
D. √ 2 cm
Bài giải: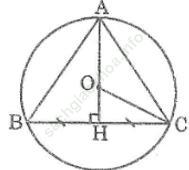
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
Bài 11 trang 158 Sách bài tập Toán 9 Tập 1: Cho hình vuông ABCD.
a. Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó
b. Tính bán kính của đường tròn đó, biết cạnh của hình vuông bằng 2cm.
Bài giải: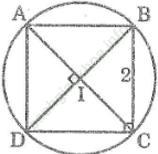
a. Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: IA = IB = IC = ID (tính chất của hình vuông)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I.
b. Áp dụng định lí Pitago vào tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = 22 + 22 = 8
Suy ra: AC = 2√ 2 (cm)
Bài 12 trang 158 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường tròn ở D.
a. Vì sao AD là đường kính của đường tròn (O)?
b. Tính số đo góc ACD
c. Cho BC = 24cm, AC = 20cm. Tính đường cao AH và bán kính đường tròn (O)
Bài giải:a. Tam giác ABC cân tại A nên AH là đường cao đồng thời cũng là đường trung trực của BC.
Vì O là tâm của đường tròn ngoại tiếp tam giác ABC nên O nằm trên đường trung trực của BC hay O thuộc AD.
Suy ra AD là đường kính của (O).
b. Tam giác ACD nội tiếp trong (O) có AD là đường kính nên suy ra góc CAD = 90o.
c. Ta có: AH ⊥ BC ⇒ HB = HC = BC/2 = 24/2 = 12 (cm)
Áp dụng định lí Pitago vào tam giác vuông ACH ta có:
AC2 = AH2 + HC2
Suy ra: AH2 = AC2 - HC2 = 202 - 122 = 400 - 144 = 256
AH = 16 (cm)
Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AC2 = AH. AD ⇒ AD = AC2/AH = 202/16 = 25 (cm)
Vậy bán kính của đường tròn (O) là: R = AD/2 = 25/2 = 12,5 (cm)
Bài 13 trang 158 Sách bài tập Toán 9 Tập 1: Tam giác ABC cân tại A, BC = 12cm, đường cao AH = 4cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.
Bài giải: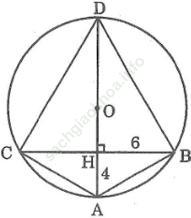
Kéo dài đường cao AH cắt đường tròn ngoại tiếp tam giác ABC tại D. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Vì tam giác ABC cân tại A nên AH là đường trung trực của BC. Suy ra AD là đường trung trực của BC.
Khi đó O thuộc AD hay AD là đường kính của đường tròn ngoại tiếp tam giác ABC.
Tam giác ACD nội tiếp trong (O) có AD là đường kính nên suy ra góc (ACD) = 90o.
Tam giác ACD vuông tại C nên theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: CH2 = HA. HD

Bài 14 trang 158 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O) và hai điểm A, B nằm bên ngoài đường tròn. Dựng đường kính COD sao cho AC = BD.
Bài giải:* Cách dựng
- Dựng A’ đối xứng với A qua tâm O của đường tròn
- Dựng đường thẳng x là trung trực của A’B
- Gọi giao điểm của đường thẳng x và đường tròn (O) là D
- Dựng đường kính COD
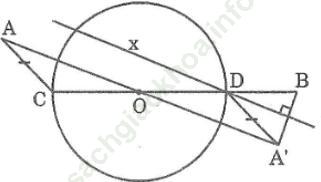
* Chứng minh
Ta có: OA = OA’ và OD = OC
Suy ra tứ giác ACA’D là hình bình hành
Suy ra: AC = A’D
Lại có: A’D = BD (tính chất đường trung trực)
Suy ra: AC = BD
Bài 1 trang 158 Sách bài tập Toán 9 Tập 1: Xét tính đúng – sai của mỗi khẳng định sau:
Cho tam giác ABC nội tiếp đường tròn (O).
a) Nếu BC là đường kính của đường tròn thì ∠ (BAC) = 90o.
b) Nếu AB = AC thì AO vuông góc với BC.
c) Nếu tam giác ABC không vuông thì điểm O nằm bên trong tam giác đó.
Bài giải:a) Đúng;
b) Sai;
c) Sai;
Bài 2 trang 158 Sách bài tập Toán 9 Tập 1: Cho tam giác ABC vuông tại A, điểm D thuộc cạnh AB, điểm E thuộc cạnh AC. Gọi M, N, P, Q theo thứ tự là trung điểm của cạnh DE, DC, BC, BE. Chứng minh rằng bốn điểm M, N, P, Q thuộc cùng một đường tròn.
Bài giải: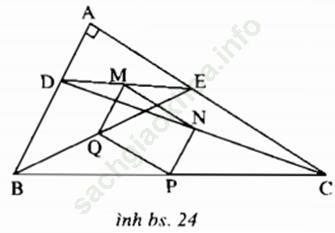
Hãy chứng minh rằng MNPQ là hình chữ nhật.
Bài 3 trang 158 Sách bài tập Toán 9 Tập 1: Cho hình thoi ABCD có ∠ A = 60o. Gọi O là giao điểm của hai đường chéo; E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Chứng minh rằng sáu điểm E, B, F, G, D, H thuộc cùng một đường tròn.
Bài giải: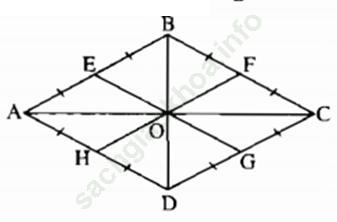
Đặt OB = OD = a. Hãy chứng minh OE = a. Tương tự, OF = OG = OH = a. Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn (O; a).