Bài 3: Liên hệ giữa phép nhân và phép khai phương - trang 9 Sách bài tập Toán 9 Tập 1

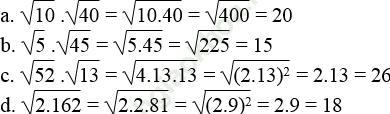
Bài 24 trang 9 Sách bài tập Toán 9 Tập 1: Áp dụng quy tắc khai phương một tích, hãy tính:

Bài giải:

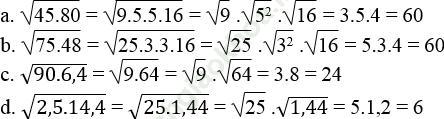
Bài 25 trang 9 Sách bài tập Toán 9 Tập 1: Rút gọn rồi tính:

Bài giải:

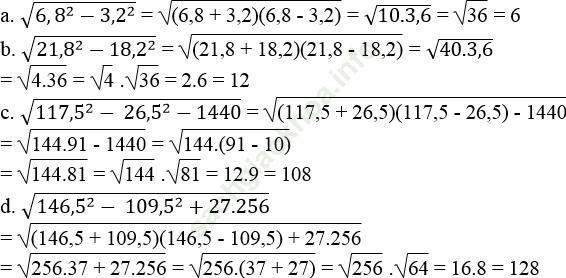
Bài 26 trang 9 Sách bài tập Toán 9 Tập 1: Chứng minh:

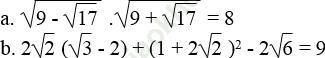
Bài giải:

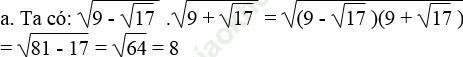
Vế trái bằng vế phải nên đẳng thức được chứng minh.

b. Ta có: 2√ 2 (√ 3 - 2) + (1 + 2√ 2)² - 2√ 6

= 2√ 6 - 4√ 2 + 1 + 4√ 2 + 8 - 2√ 6 = 1 + 8 = 9

Vế trái bằng vế phải nên đẳng thức được chứng minh.

Bài 27 trang 9 Sách bài tập Toán 9 Tập 1: Rút gọn:

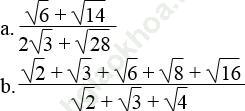
Bài giải:

Bài 28 trang 9 Sách bài tập Toán 9 Tập 1: So sánh (không dùng bảng số hay máy tính bỏ túi):

a. √ 2 + √ 3 và √ 10

b. √ 3 + 2 và √ 2 + √ 6

c. 16 và √ 15. √ 17

d. 8 và √ 15 + √ 17

Bài giải:

a. √ 2 + √ 3 và √ 10

Ta có: (√ 2 + √ 3)² = 2 + 2√ 6 + 3 = 5 + 2√ 6

(√ 10)² = 10 = 5 + 5

So sánh 2√6 và 5:

Ta có: (2√ 6)² = 2². (√ 6)² = 4.6 = 24

5² = 25

Vì (2√ 6)² < 5² nên 2√ 6 < 5

Vậy 5 + 2√ 6 < 5 + 5 ⇒ (√ 2 + √ 3)² < (√ 10)² ⇒ √ 2 + √ 3 < √ 10

b. √ 3 + 2 và √ 2 + √ 6

Ta có: (√ 3 + 2)² = 3 + 4√ 3 + 4 = 7 + 4√ 3

(√ 2 + √ 6)² = 2 + 2√ 12 + 6 = 8 + 2√ (4.3) = 8 + 2. √ 4. √ 3 = 8 + 4√ 3

Vì 7 + 4√ 3 < 8 + 4√ 3 nên (√ 3 + 2)² < (√ 2 + √ 6)²

Vậy √ 3 + 2 < √ 2 + √ 6

c. 16 và √ 15. √ 17

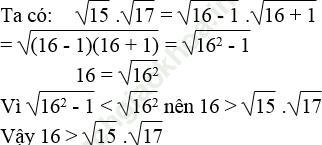
d. 8 và √ 15 + √ 17

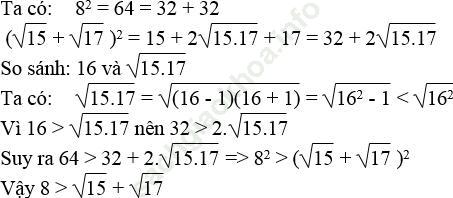
Bài 29 trang 9 Sách bài tập Toán 9 Tập 1: So sánh (không dùng bảng số hay máy tính bỏ túi):

√ 2003 + √ 2005 và 2√ 2004

Bài giải: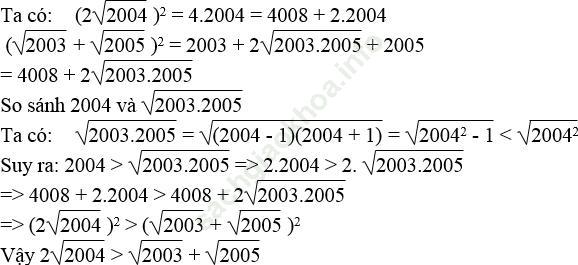

Bài 30 trang 9 Sách bài tập Toán 9 Tập 1: Cho các biểu thức:

a. Tìm x để A có nghĩa. Tìm x để B có nghĩa

b. Với giá trị nào của x thi A = B?

Bài giải: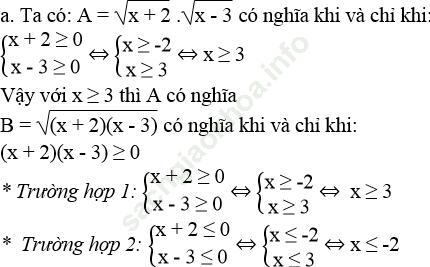

Vậy với x ≥ 3 hoặc x ≤ -2 thì B có nghĩa.

b. Để A và B đồng thời có nghĩa thì x ≥ 3

Vậy với x ≥ 3 thì A = B.

Bài 31 trang 10 Sách bài tập Toán 9 Tập 1: Biểu diễn ở dạng tích các căn bậc hai với a < 0 và b < 0.

Bài giải:

Vì a < 0 nên -a > 0 và b < 0 nên -b > 0

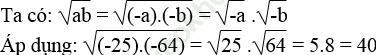
Bài 32 trang 10 Sách bài tập Toán 9 Tập 1: Rút gọn các biểu thức:

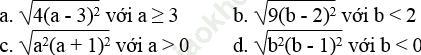
Bài giải:

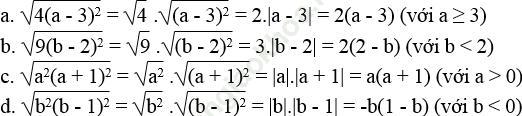
Bài 33 trang 10 Sách bài tập Toán 9 Tập 1: Tìm điều kiện của x để các biểu thức sau có nghĩa và biến đổi chúng về dạng tích:

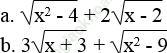
Bài giải:

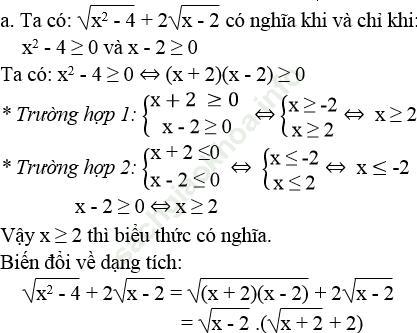
Bài 34 trang 10 Sách bài tập Toán 9 Tập 1: Tìm x, biết:

Bài giải:

Bài 35 trang 10 Sách bài tập Toán 9 Tập 1: Với n là số tự nhiên, chứng minh:

Viết đẳng thức trên khi n bằng 1,2,3,4

Bài giải:

Ta có:

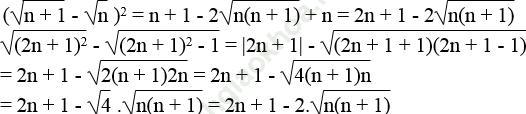
Vế trái bằng vế phải nên đẳng thức được chứng minh.

* Với n = 1, ta có: (√ 2 - √ 1)² = √ 9 - √ 8

* Với n = 2, ta có: (√ 3 - √ 2)² = √ 25 - √ 24

* Với n = 3, ta có: (√ 4 - √ 3)² = √ 49 - √ 48

* Với n = 4, ta có: (√ 5 - √ 4)² = √ 81 - √ 80

Bài tập bổ sung:

Bài 1 trang 10 Sách bài tập Toán 9 Tập 1: Giá trị của √ 1,6. √ 2,5 bằng

A. 0,20;

B. 2,0;

C. 20,0;

C. 0,02.

Hãy chọn đáp án đúng.

Bài giải:

Đáp án đúng là: B. 2,0