Bài 8: Đường tròn (trang 94 SBT Toán 6 Tập 2)
Bài 35 trang 93 sách bài tập Toán 6 Tập 2: Cho 2 điểm A và B cách nhau 3cm. Vẽ đường tròn (A; 2,5cm) và đường tròn (B; 1,5cm). 2 đường tròn này giao nhau tại điểm C và D.
a) Tính CA, DB.
b) Tại sao đường tròn (B; 1,5cm) giao với đoạn thẳng AB tại trung điểm I của đoạn thẳng AB?
c) Đường tròn (A; 2,5cm) cắt đoạn thẳng AB tại điểm K. Tính đoạn thẳng KB
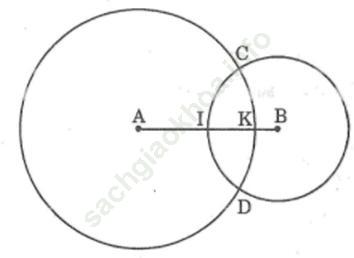
Đáp án:
a) Vì điểm C nằm trên đường tròn (A; 2,5cm) do đó CA = 2,5cm
Điểm D nằm trên đường tròn (B; 1,5cm) do đó đoạn thẳng DB = 1,5 cm
b) Vì điểm I nằm giữa hai điểm A và B do đó AB = IA + IB
=> AI = AB – BI = 3 – 1,5 = 1,5 (cm)
Vì IA = IB = 1,5 cm
Nên điểm I là trung điểm của đoạn thẳng AB.
c) Vì điểm K nằm giữa hai điểm A và B nên: AK + KB = AB
=> KB = AB – AK = 3 – 2,5 = 0,5 (cm)
Bài 36 trang 93 sách bài tập Toán 6 Tập 2: So sánh các đoạn thẳng trong hình bên bằng mắt sau đó kiểm tra lại kết quả bằng compa.
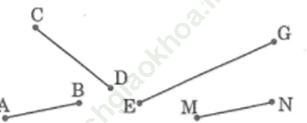
Đáp án:
Dùng mắt quan sát và ước lượng độ dài của các đoạn thẳng, sau đó sử dụng compa để kiểm tra lại xem có đúng như ước lượng không. Kết quả thấy rằng đoạn thẳng EG dài nhất, sau đó là đoạn CD, cuối cùng là 2 đoạn thẳng bằng nhau MN và AB.
Bài 37 trang 93 sách bài tập Toán 6 Tập 2: Làm thế nào để chỉ cần đo 1 lần, mà có thể biết được tổng độ dài các đoạn thẳng ở hình bên.
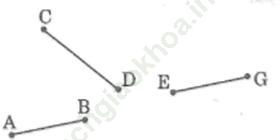
Đáp án:
Kẻ tia Oy. Sử dụng compa đặt các đoạn AB, CD và EG liên tiếp trên tia Oy sao cho điểm A trùng với điểm O, điểm C trùng với điểm B, điểm E trùng với điểm D. Đo đoạn thẳng OG. Độ dài của đoạn thẳng OG chính là độ dài 3 đoạn thẳng trên
Bài 38 trang 93 sách bài tập Toán 6 Tập 2: a) Vẽ đoạn thẳng AB có độ dài bằng 3cm.
b) Vẽ đường tròn tâm A có bán kính bằng 2cm.
c) Vẽ đường tròn tâm B có bán kính bằng 2cm.
d) Đặt tên giao điểm của 2 đường tròn là C và D.
e) Vẽ đoạn thẳng CD.
g) Đặt tên giao điểm của CD và AB là I.
h) Đo hai đoạn thẳng IA và IB.
Đáp án: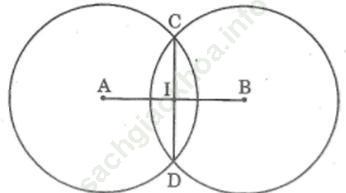
Ta có: IA = IB = 3/2 = 1,5 cm
Bài 39 trang 93 sách bài tập Toán 6 Tập 2: Vẽ lại các hình dưới đây (cho đúng kích thước như hình đã cho).
Đáp án:
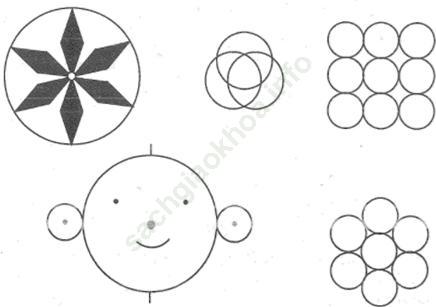
Sử dụng các loại dụng cụ để vẽ lại các hình như trên
Bài 1 trang 94 sách bài tập Toán 6 Tập 2: Vẽ hình liên tiếp theo các cách diễn đạt dưới đây
a) Vẽ đoạn thẳng AB bằng 2cm. Vẽ đường tròn (c1) tâm A có bán kính là AB.
b) Vẽ đường tròn (c2) tâm B có bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (c1) là điểm G và C.
c) Vẽ đường tròn (c3) tâm C có bán kính AC. Goi giao điểm mới của đường tròn này với đường tròn (c1) là điểm D.
d) Vẽ đường tròn (c4) tâm D có bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là điểm E.
e) Vẽ đường tròn (c5) tâm E, bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là điểm F
f) Vẽ đường tròn (c6) tâm F, bán kính AF.
g) Vẽ đường tròn (c7) tâm G, bán kính AG.
Sau khi vẽ hình trên hãy so sánh các đoạn thẳng sau: CD, DE, EF, FG, AB, BC, GBĐáp án:
Sau khi vẽ ta sẽ được hình bs. 17
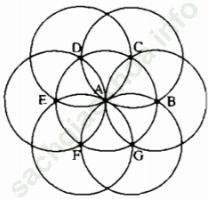
Khi đó, các đoạn thẳng sau: CD, EF, AB, BC, FG, GB bằng nhau (vì cùng bằng bán kính).
Bài 2 trang 95 sách bài tập Toán 6 Tập 2: Vẽ đường tròn tâm O, bán kính R = 3cm. Vẽ một đường kính AB. Vẽ tiếp một dây cung CD (hai điểm C, D không trùng với các điểm A, B và ba điểm C, O, D không thẳng hàng)
a) Đọc tên các cung có các đầu mút là hai trong số các điểm A, B, C, D.
b) So sánh độ dài của hai dây AB và CD.
c) Nếu lấy n điểm (phân biệt) trên đường tròn đó ta có được bao nhiêu cung.
Đáp án:
Giả sử vẽ được như hình bs. 18
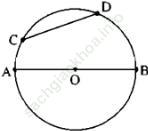
a) Khi đó, có các cung là: AD nhỏ, AC nhỏ, AB hay cung ACDBm BA (cung nửa đường tròn không đi qua C và D), ABD hay cung AD lớn, ABDC hay cung AC lớn, BD nhỏ, BC nhỏ, BAC hay cung BC lớn, BACD hay cung BD lớn, CD nhỏ, CABD hay CD lớn.
b) Sử dụng compa so sánh được CD < AB.
c) Với 2 điểm (phân biệt) trên 1 đường tròn ta có được 2 cung có mút là 2 điểm đó. Với n điểm (phân biệt) cho trước trên 1 đường tròn, thì cứ lấy hai trong số n điểm đó ta được hai cung, chính vì vậy có tất cả n (n – 1) cung trên đường tròn đó.
Bài 3 trang 95 sách bài tập Toán 6 Tập 2: Lấy 3 điểm là A, B, C bất kỳ, không thẳng hàng.
Vẽ các đoạn thẳng là AB, BC, CA.
a) Sử dụng compa để dựng đoạn MP = AB + BC
b) Sử dụng compa để so sánh AC với AB + BC
Đáp án:
Vẽ đường thẳng k không cắt ba đoạn thẳng AB, BC, CA (xem hình bs. 19)
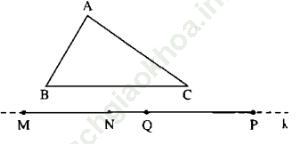
Lấy 1 điểm M trên đường thẳng k.
a) Sử dụng compa dựng đoạn thẳng MN = AB; tiếp theo dựng đoạn thẳng NP = BC (điểm N nằm giữa 2 điểm M, P) Khi đó, ta có MP = AB + BC.
b) Tiếp tục, sử dụng compa dựng đoạn thẳng MQ = AC. Khi đó ta có thể thấy ngay điểm Q nằm giữa 2 điểm M. P tức là MQ < MP, từ đó => AC < AB + BC.