Bài 13: Bội và ước của một số nguyên (trang 91 SBT Toán 6 Tập 1)
Bài 150 trang 91 SBT Toán 6 Tập 1: Tìm năm bội của 2 và -2:
Đáp án:
* Bội của 2 có dạng là 2k với k ∈ Z.
Với mỗi giá trị nguyên của k sẽ cho ta 1 số là bội của 2.
Ta sẽ tìm được 5 bội của 2 là: - 2; 0; 2; 4; 6.
(tương ứng với k = -1; 0; 1; 2; 3)
* Bội của -2 có dạng -2k với k ∈ Z.
Với mỗi giá trị nguyên của k cho ta 1 bội của -2.
Ta tìm được 5 bội của - 2 là: -6; - 4; - 2; 0; 2.
(Tương ứng với k = 3; 2; 1; 0; -1)
Bài 151 trang 91 SBT Toán 6 Tập 1: Tìm tất cả các ước của các số sau: -2; 4; 13; 15; 1
Đáp án:Ư (-2) = {-2; -1; 1; 2}
Ư (4) = {-4; -2; -1; 1; 2; 4}
Ư (13) = {-13; -1; 1; 13}
Ư (15) = {-15; -5; -3; -1; 1; 3; 5; 15}
Ư (1) = {1; -1}
Bài 152 trang 91 SBT Toán 6 Tập 1: Cho 2 tập số sau: A = {4; 5; 6; 7; 8}; B = {13; 14; 15}
a. Có thể lập được tất cả bao nhiêu tổng dưới dạng (a + b) với a ∈ A; b∈ B
b. Trong các tổng trên, có bao nhiêu tổng chia hết cho 3?
Đáp án:Những giá trị của a, b và a + b đã được thể hiện trong bảng dưới đây:
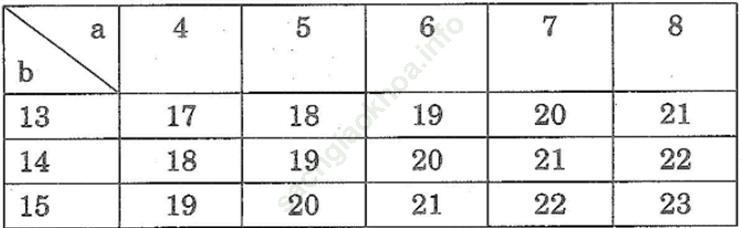
a. Có tất cả 15 tổng với 7 giá trị khác nhau được tạo thành
b. Trong số đó, các tổng 18; 18; 21; 21; 21 là các số chia hết cho 3.
Vậy có tất cả 5 tổng với 2 giá trị khác nhau (là 18; 21) chia hết cho 3
Bài 153 trang 91 SBT Toán 6 Tập 1: Tìm số nguyên x, biết rằng:
a. 12. x = -36
b. 2. |x| = 16
Đáp án:a. 12. x = -36
< => x = (-36): 12
=> x = -3
b. 2. |x| = 16
< => |x| = 16: 2
=> |x| = 8
Vậy nên x = 8 hoặc x = -8
Bài 154 trang 91 SBT Toán 6 Tập 1: Điền vào ô trống:
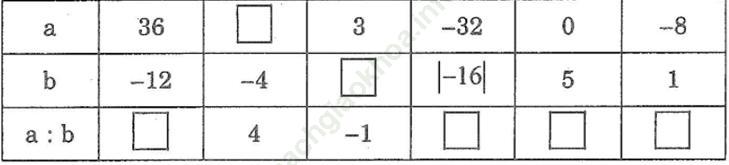
Đáp án:
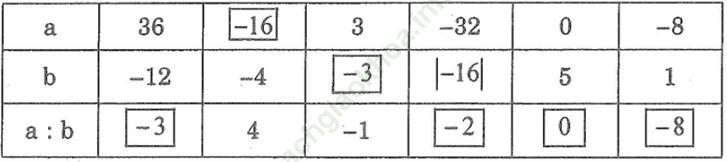
Bài 155 trang 91 SBT Toán 6 Tập 1: Tìm 2 cặp số nguyên a, b khác nhau thỏa mãn a ⋮ b và b ⋮ a
Đáp án:* Với tất cả các số nguyên a khác 0. Số đối của a là – a và ta có:
(-a) = (-1).a và a = (-1). (-a)
=> (-a) chia hết cho a và ngược lại a chia hết cho (-a)
Hay nói cách khác 2 số đối nhau và khác 0 đều có tính chất số thứ nhất chia hết cho số thứ 2 và số thứ 2 chia hết cho số thứ nhất.
Ví dụ: (-3) ⋮ 3 và 3 ⋮ (-3)
(-11) ⋮ 11 và 11 ⋮ (-11)
Bài 156 trang 91 SBT Toán 6 Tập 1: Điền chữ “S” (sai) hoặc “Đ” (đúng) vào các ô vuông:
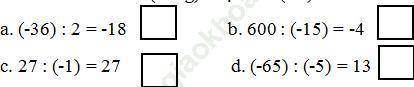
Đáp án:
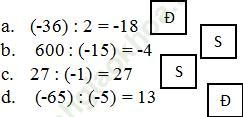
Bài 157 trang 91 SBT Toán 6 Tập 1: Tính giá trị của các biểu thức:
a. [ (-23).5]: 5
b. [32. (-7)]: 32
Đáp án:a. [(-23).5]: 5 = (-23). (5: 5) = (-23).1 = -23
b. [32. (-7)]: 32 = (-7). (32: 32) = (-7).1 = -7
Bài 158 trang 91 SBT Toán 6 Tập 1: Điền số thích hợp vào các ô trống trong hình dưới đây:
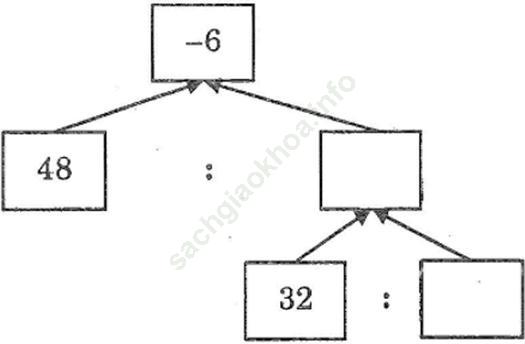
Đáp án:
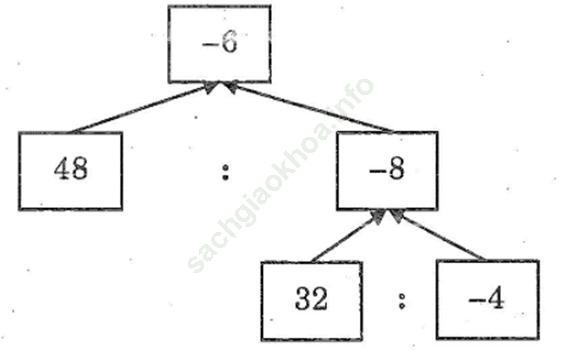
Bài 13.1 trang 92 SBT Toán 6 Tập 1: Điền vào chỗ chấm:
a) Số... là bội của tất cả các số nguyên khác 0;
b) Số... không phải là ước của bất kì số nguyên nào;
c) Các số.............. là ước của tất cả các số nguyên.
Đáp án:a) Số 0 là bội của tất cả các số nguyên khác 0;
b) Số 0 không phải là ước của bất kì số nguyên nào;
c) Các số 1, -1 là ước của tất cả các số nguyên.
Bài 13.2 trang 92 SBT Toán 6 Tập 1: Tìm các số nguyên x thoả mãn:
a) (x + 4) ⋮ (x + 1);
b) (4x + 3) ⋮ (x - 2).
Đáp án:a) Ta có x + 4 = (x + 1) + 3
nên (x + 4) ⋮ (x + 1) khi 3 ⋮ (x + 1), cũng có nghĩa là x + 1 là ước của 3.
Vì Ư (3) = {-1; 1; -3; 3} nên ta có bảng sau đây:

Đáp số x = -4; -2; 0; 2.
b) Ta có 4x + 3 = 4 (x - 2) + 11
do đó (4x + 3) ⋮ (x - 2) khi 11 ⋮ (x - 2), có nghĩa là x -2 là ước của 11
Ư (11) = {-11; -1; 1; 11}; ta có bảng dưới đây:

Vậy các số nguyên x thỏa mãn điều kiện là: x ∈ {1; 3; - 9; 13}
Bài 13.3 trang 92 SBT Toán 6 Tập 1: Tìm số nguyên x, biết rằng:
a) 2|x + 1|=10;
b) (-12)2.x = 56 + 10.13. x
Đáp án:a) 2. |x + 1| = 10
< => | x + 1| = 10: 2
< => |x + 1| = 5
* Trường hợp 1: x + 1 = 5
< => x = 5 – 1 => x = 4
* Trường hợp 2: x + 1 = -5
< => x = - 5 - 1 => x = -6
Vậy x = - 6 hoặc x = 4
b) (-12)2. x = 56 + 10.13. x
< => 144. x = 56 + 130. x
< => 144x – 130 x = 56
< => 14x = 56
< => x = 56: 14
=> x = 4
Vậy x = 4
Bài trước: Bài 12: Tính chất của phép nhân (trang 85 SBT Toán 6 Tập 1) Bài tiếp: Ôn tập chương 2 Số học (trang 93 SBT Toán 6 Tập 1)