Bài 10: Tính chất chia hết của một tổng (trang 20 SBT Toán 6 Tập 1)
Bài 114 trang 20 SBT Toán 6 Tập 1: Áp dụng tính chất chia hết, xét xem từng tổng (hiệu) sau có chia hết cho 6 không?
a. 42 + 54
b. 600 – 14
c. 120 + 48 + 20
d. 60 + 15 + 3
Đáp án:a. Vì 54 ⋮ 6 và 42 ⋮ 6 vậy nên (42 + 54) ⋮6
b. Vì 600 ⋮ 6 nhưng 14 không chia hết cho 6 vậy nên (600 -14) không chia hết cho 6.
c. Vì 120 ⋮ 6 và 48 ⋮ 6 nhưng 20 không chia hết cho 6 vậy nên (120 + 48 + 20) không chia hết cho 6
d. Vì 15 + 3 = 18 ⋮ 6 và 60 ⋮ 6 nên (60 + 15 + 3) ⋮ 6
Bài 115 trang 20 SBT Toán 6 Tập 1: Cho tổng A = 12 + 15 + 21 + x, với x ∈ N. Tìm điều kiện của x để A không chia hết cho 3, để A chia hết cho 3.
Đáp án:Ta có: 15 ⋮ 3; 21 ⋮3 và 12 ⋮ 3
=> A = (12 + 15 + 21 + x) ⋮3 nếu x ⋮ 3
A = (12 + 15 + 21 + x) không chia hết cho 3 nếu x là số không chia hết cho 3
Bài 116 trang 20 SBT Toán 6 Tập 1: Khi chia số tự nhiên a cho 24, ta được số dư là 10. Hỏi số a đó có chia hết cho 2 không? Có chia hết cho 4 không?
Đáp án:Ta có: a chia cho 24 được thương là k và số dư là 10 nên:
a = 24k + 10 (k ∈ N)
Vì 24 ⋮ 2 và 10 ⋮ 2 nên (24k + 10) ⋮ 2
Vì 24 ⋮ 4 nhưng 10 không chia hết cho 4 nên tổng (24k + 10) không chia hết cho 4
Bài 117 trang 20 SBT Toán 6 Tập 1: Viết dấu “x” vào ô thích hợp:

Đáp án:

Bài 118 trang 20 SBT Toán 6 Tập 1: Chứng minh rằng:
a. Trong hai số tự nhiên liên tiếp, có 2 số chia hết cho 2.
b. Trong 3 số tự nhiên liên tiếp, có 1 số chia hết cho 3.
Đáp án:a. Gọi 2 số tự nhiên liên tiếp là a và a + 1
Bài toán được chứng minh nếu a chia hết cho 2.
a = 2k + 1 (k∈ N) trong trường hợp a không chia hết cho 2
=> a + 1 = 2k + 1 + 1 = 2k + 2
Ta có: 2k ⋮ 2; 2 ⋮ 2
=> (a + 1) ⋮ 2 hay (2k + 2) ⋮ 2
Vậy trong 2 số tự nhiên liên tiếp, có 1 số chia hết cho 2
b. Gọi 3 số tự nhiên liên tiếp là a, a + 1, a + 2
Bài toán được chứng minh nếu a chia hết cho 3
a = 3k + 1 hoặc a = 3k + 2 (k ∈ N) nếu a không chia hết cho 3
Nếu a = 3k + 1 thì a + 2 = 3k + 1 + 2 = 3k + 3 ⋮ 3
(vì 3 ⋮ 3 và 3k ⋮ 3 nên 3k + 3 ⋮ 3)
Nếu a = 3k + 2 thì a + 1 = 3k + 2 + 1 = 3k + 3 ⋮ 3
(vì 3 ⋮ 3 và 3k ⋮ 3 nên 3k + 3 ⋮ 3)
Vậy trong 3 số tự nhiên liên tiếp, có 1 số chia hết cho 3
Bài 119 trang 21 SBT Toán 6 Tập 1: Chứng minh rằng:
a. Tổng của 3 số tự nhiên liên tiếp là 1 số chia hết cho 3
b. Tổng của 4 số tự nhiên liên tiếp là 1 số không chia hết cho 4
Đáp án:a. Gọi 3 số tự nhiên liên tiếp là: a, a + 1, a + 2
Ta có: a + (a+ 1) + (a + 2) = (1+ 2) + (a + a + a) = 3a + 3
Vì 3a⋮3 và 3 ⋮3 => (3a + 3) ⋮3
Vậy tổng của 3 số tự nhiên liên tiếp chia hết cho 3
b. Gọi 4 số tự nhiên liên tiếp là a, a + 1, a + 2 và a + 3
Ta có; a + (a + 1) + (a + 2) + (a + 3) = (1+ 2+3) + (a + a + a +a) = 6 +4a
Vì 4a ⋮ 4 nhưng 6 không chia hết cho 4 nên (4a + 6) cũng không chia hết cho 4
Bài 120 trang 21 SBT Toán 6 Tập 1: Chứng minh rằng số có dạng (aaaaaa) bao giờ cũng chia hết cho 7 (ví dụ 333333 ⋮7)
Đáp án:Ta có: (aaaaaa) = 111111. a = 3.7.11.13.37. a
Vì 3.7.11.13.37. a ⋮7 do đó 111111. a ⋮7.
Vậy kết luận rằng số có dạng (aaaaaa) bao giờ cũng chia hết cho 7
Bài 121 trang 21 SBT Toán 6 Tập 1: Chứng minh rằng số có dạng (abcabc) bao giờ cũng chia hết cho 11 (ví dụ 328328 ⋮11)
Đáp án: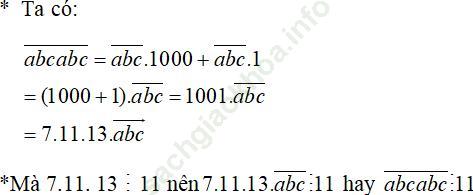
Bài 122 trang 21 SBT Toán 6 Tập 1: Chứng minh rằng lấy 1 số có 2 chữ số, cộng với số gồm 2 chữ số ấy viết theo thứ tự ngược lại, ta luôn luôn được 1 số chia hết cho 11 (ví dụ 37 + 73 = 110, chia hết cho 11)
Đáp án:Gọi số tự nhiên có 2 chữ số là ab (a ≠ 0)
Số viết theo thứ tự ngược lại của ab chính là ba
Ta có:ba = 10b + a và ab = 10a + b
Vì vậy: ab+ ba= (10b + a) + (10a + b)= 11a + 11b = 11. (a + b)
Vì 11. (a + b) ⋮ 11 nên suy ra ab + ba luôn chia hết cho 11
Bài 10.1 trang 21 SBT Toán 6 Tập 1: Điền các từ thích hợp (chia hết, không chia hết) vào chỗ chấm:
a) Nếu b ⋮ m, c ⋮ m, a ⋮ m thì tổng a + b + c... cho m;
b) Nếu a ⋮ 5, b ⋮ 5, c ∕⋮ 5 thì tích a. b. c... cho 5;
c) Nếu a ⋮ 3 và b ∕⋮ 3 thì tích a. b.... cho 3.
Đáp án:a) Chia hết
b) Chia hết
c) Chia hết
Bài 10.2 trang 21 SBT Toán 6 Tập 1: Chứng minh rằng nếu 2 số có cùng số dư khi chia cho 7 thì hiệu của chúng cũng chia hết cho 7
Đáp án:Gọi a và b là 2 số có cùng số dư là r khi chia cho 7 (giả sử a ≥ b)
Ta có a = 7m + r và b = 7n + r (m, n ∈ N)
Khi đó a - b = (7m + r) - (7n + r) = 7m - 7n = 7. (m – n)
Ta có: 7 ⋮ 7 nên suy ra a - b ⋮ 7 hay 7 (m - n) ⋮ 7
Bài 10.3 trang 21 SBT Toán 6 Tập 1: Chứng minh rằng số có dạng aaa bao giờ cũng chia hết cho 37.
Đáp án:Ta có: aaa = 10. a + a + 100. a= (100 + 10 + 1).a = 111. a = 3.37. a ⋮ 37 (điều phải chứng minh)
Bài 10.4 trang 21 SBT Toán 6 Tập 1: Chứng minh rằng hiệu ab− ba (với a ≥ b) bao giờ cũng chia hết cho 9.
Đáp án:Ta có: ab− ba = (10a + b) - (10b + a) = 9a - 9b = 9 (a - b) chia hết cho 9 (điều phải chứng minh).
Bài trước: Bài 9: Thứ tự thực hiện các phép tính (trang 18 SBT Toán 6 Tập 1) Bài tiếp: Bài 11: Dấu hiệu chia hết cho 2, cho 5 (trang 21 SBT Toán 6 Tập 1)