Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số - Giải bài tập Toán 12
Bài 5 trang 32 sách giáo khoa Toán 12 Giải tích:
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số đã học theo sơ đồ trên.
y = ax + b
y = ax2 + bx + c
Lời giải:* Hàm số y = ax + b
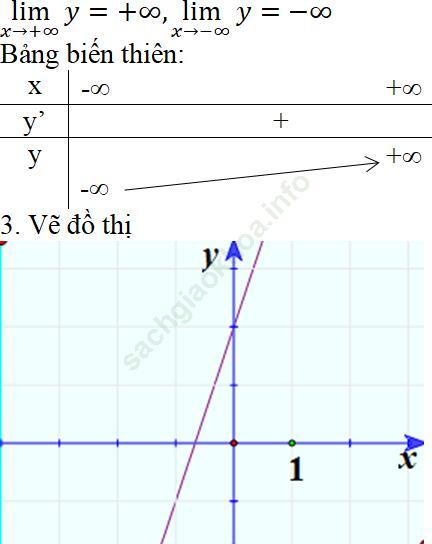
Trường hợp a > 0
1. Tập xác định: D = R.
2. Sự biến thiên.
y’ = a > 0. Vậy hàm số đồng biến trên toàn bộ R.
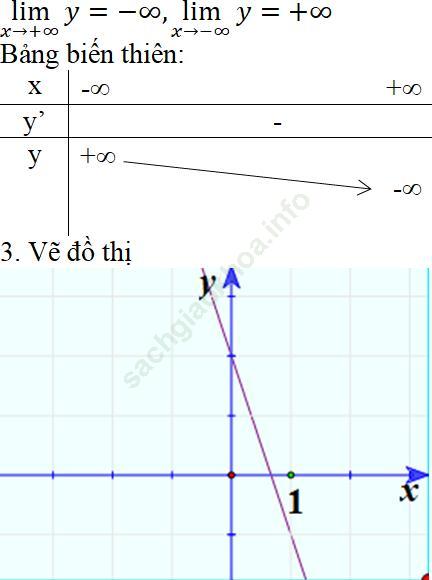
Trường hợp a < 0
1. Tập xác định: D = R.
2. Sự biến thiên.
y’ = a < 0. Vậy hàm số đồng biến trên toàn bộ R.
* Hàm số y = ax2 + bx + c
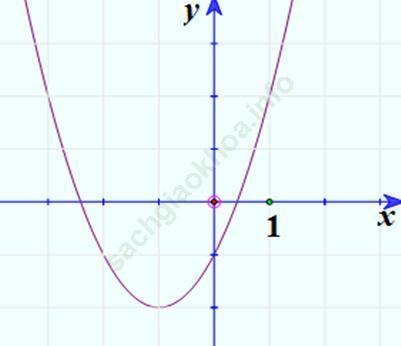
Trường hợp a > 0
1. Tập xác định: D = R.
2. Sự biến thiên.
y’ = 2ax + b. Cho y’ = 0 thì x = - b/2a.
Hàm số nghịch biến trên khoảng (-∞, - b/2a).
Hàm số đồng biến trên khoảng [- b/2a, +∞].
Hàm số đạt cực tiểu bằng - Δ /4a tại x = - b/2a.
3. Vẽ đồ thị:
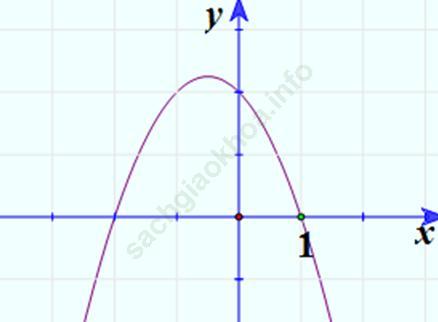
Trường hợp a < 0
1. Tập xác định: D = R.
2. Sự biến thiên.
y’ = 2ax + b. Cho y’ = 0 thì x = - b/2a.
Hàm số đồng biến trên khoảng (-∞, - b/2a).
Hàm số nghịch biến trên khoảng [- b/2a, +∞].
Hàm số đạt cực đại bằng - Δ /4a tại x = - b/2a.
3. Vẽ đồ thị:
Bài 5 trang 33 sách giáo khoa Toán 12 Giải tích
Câu hỏi:Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x3 + 3x2 – 4. Nêu nhận xét về đồ thị của hàm số này với đồ thị của hàm số khảo sát trong Ví dụ 1.
Lời giải:1. Tập xác định: D = R.
2. Sự biến thiên:
y’ = -3x2 + 6x. Cho y’ = 0 ⇒ x = 0 hoặc x = 2.
Bảng biến thiên:
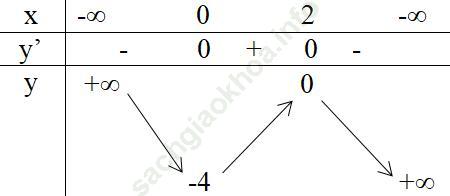
Hàm số đồng biến trên khoảng (0,2)
Hàm số nghịch biến trên các khoảng (-∞, 0), (2, + ∞).
Hàm số đạt cực đại bằng 0 tại x = 2.
Hàm số đạt cực tiểu bằng -4 tại x = 0.
3. Vẽ đồ thị
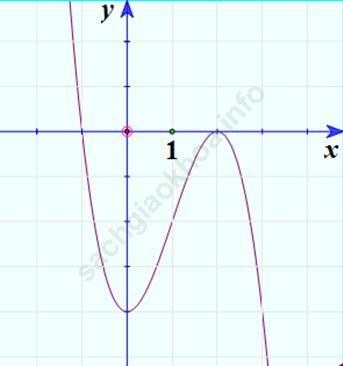
Nhận xét: Hai đồ thị đối xứng nhau qua Oy.
Bài 5 trang 35 sách giáo khoa Toán 12 Giải tích
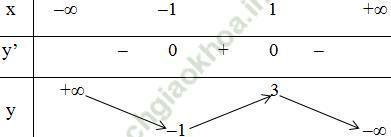
Câu hỏi:Khảo sát sự biến thiên và vẽ đồ thị hàm số y = x3/3 - x2 + x + 1.
Lời giải:1. Tập xác định: D = R.
2. Sự biến thiên:
y’ = x2 – 2x + 1 = (x - 1)2 ≥ 0 với mọi x. Vậy hàm số đồng biến trên toàn bộ R.
Cho y’ = 0 ⇒ x = 1.
Bảng biến thiên
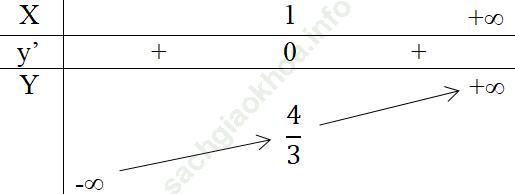
3. Vẽ đồ thị
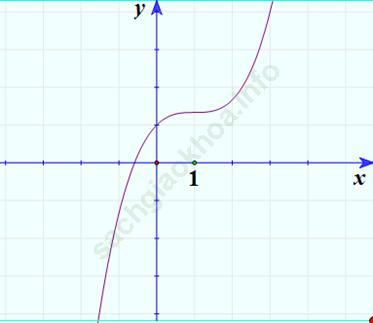
Bài 5 trang 36 sách giáo khoa Toán 12 Giải tích
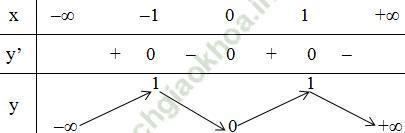
Câu hỏi:Trả lời câu hỏi Toán 12 Giải tích Bài 5 trang 36: Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x4 + 2x2 + 3.
Bằng đồ thị, biện luận theo m số nghiệm của phương trình -x4 + 2x2 + 3 = m.Lời giải:
1. Tập xác định: D = R.
2. Sự biến thiên:
y’ = -4x3 + 4x. Cho y’ = 0 ⇒ x = 0 hoặc x = ± 1.
Bảng biến thiên:
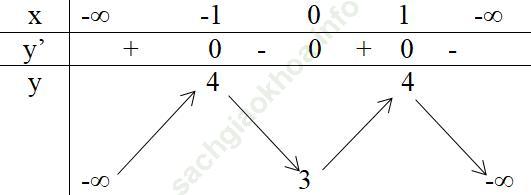
Hàm số đồng biến trên: (-∞, -1), (0,1).
Hàm số nghịch biến trên: (-1,0), (1, +∞).
Hàm số đạt cực đại bằng 4 tại x = -1 và x = 1.
Hàm số đạt cực tiểu bằng 3 tại x = 0.
3. Vẽ đồ thị
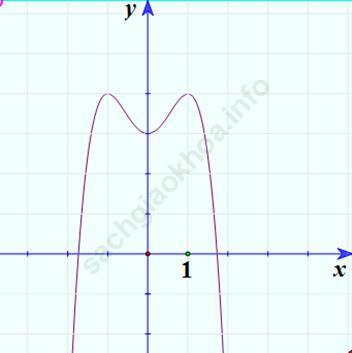
4. Biện luận phương trình -x4 + 2x2 + 3 = m.
Số giao điểm của hai đồ thị y = -x4 + 2x2 + 3 và y = m là số nghiệm của phương trình trên.
Với m > 4. Hai đồ thị không giao nhau nên phương trình vô nghiệm.
Với m = 4 và m < 3. Hai đồ thị giao nhau tại 2 điểm phân biệt nên phương trình có hai nghiệm phân biệt.
Với m = 3. Hai đồ thị giao nhau tại 3 điểm phân biệt nên phương trình có ba nghiệm phân biệt.
Với 3 < m < 4. Hai đồ thị giao nhau tại 4 điểm phân biệt nên phương trình có bốn nghiệm phân biệt.
Bài 5 trang 38 sách giáo khoa Toán 12 Giải tích
Câu hỏi:Lấy một ví dụ về hàm số dạng y = ax4 + bx2 + c sao cho phương trình y’ = 0 chỉ có một nghiệm.
Lời giải:Ví dụ hàm số y = x4. Có đạo hàm y’ = 4x3. Cho y’ = 0 thì x = 0.
Bài 5 trang 42 sách giáo khoa Toán 12 Giải tích
Câu hỏi:Tìm tọa độ giao điểm của đồ thị hai hàm số:
y = x2 + 2x – 3
y = -x2 – x + 2.
Lời giải:Xét phương trình tương giao:
-x2 – x + 2 = x2 + 2x – 3 ⇔ 2x2 + 3x – 5 = 0
Khi và chỉ khi x = 1 hoặc x = -5/2.
Vậy tọa độ giao điểm là (1,0) và (-5/2,8.25).
Áp dụng kiến thức sau để giải các bài tập phía dưới:
Các bước khảo sát hàm số và vẽ đồ thị:
1, Tìm tập xác định.
2, Khảo sát sự biến thiên
+ Tính y’
⇒ Chiều biến thiên của hàm số.
+ Tìm cực trị.
+ Tính các giới hạn
Từ đó suy ra Bảng biến thiên.
3, Vẽ đồ thị hàm số.
Bài 1 trang 43 sách giáo khoa Toán Giải tích 12
a) y = 2 + 3x - x3;
b) y = -x3 + 4x2 - 4x
c) y = x3 + x2 + 9x;
d) y = -2x3 + 5
Lời giải:
a) Hàm số y = -x3 + 3x + 2.
1) Tập xác định: D = R
2) Sự biến thiên:
- Chiều biến thiên:
y' = -3x2 + 3.
y' = 0 ⇔ x = ±1.
Trên các khoảng (-∞; -1) và (1; +∞), y’ < 0 nên hàm số nghịch biến.
Trên (-1; 1), y’ > 0 nên hàm số đồng biến.
- Cực trị:
Hàm số đạt cực đại tại x = 1, yCĐ = 4;
Hàm số đạt cực tiểu tại x = -1; yCT = 0.
- Giới hạn:
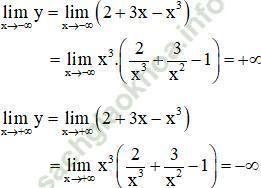
- Bảng biến thiên:
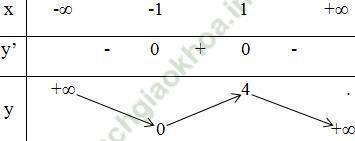
3) Vẽ đồ thị:
Ta có: 2 + 3x – x3 = 0 ⇔ 
Vậy giao điểm của đồ thị với trục Ox là (2; 0) và (-1; 0).
y (0) = 2 ⇒ giao điểm của đồ thị với trục Oy là (0; 2).
Đồ thị hàm số:
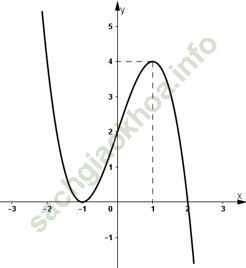
b) Hàm số y = -x3 + 4x2 - 4x.
1) Tập xác định: D = R
2) Sự biến thiên:
y' = -3x2 + 8x - 4;
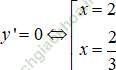
Trên các khoảng (-∞; 2/3) và (2; +∞) thì y’ < 0 nên hàm số nghịch biến.
Trên (2/3; 2) thì y’ > 0 nên hàm số đồng biến.
- Cực trị:
Hàm số đạt cực đại tại x = 2, fCD = 0;
Hàm số đạt cực tiểu tại x = 2/3; fCT = 
- Giới hạn:
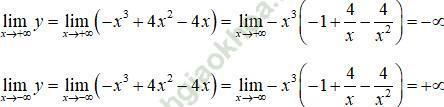
- Bảng biến thiên:
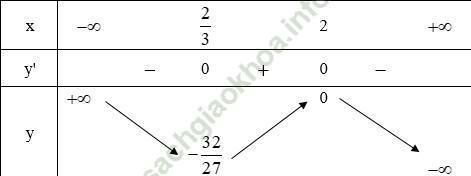
3) Vẽ đồ thị:
Ta có: -x3 + 4x2 - 4x = 0 ⇔ -x (x - 2)2 = 0 ⇔ 
Vậy giao điểm của đồ thị với Ox là (0; 0) và (2; 0).
- y (1) = -1. Vậy (1; -1) thuộc đồ thị hàm số.
- y (3) = -3. Vậy (3; -3) thuộc đồ thị hàm số
- y (-1) = -1 ⇒ (-1; -1) thuộc đồ thị hàm số
Vẽ đồ thị hàm số:
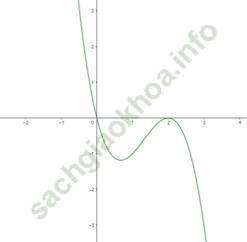
c) Hàm số y = x3 + x2 + 9x.
1) Tập xác định: D = R
2) Sự biến thiên:
- Chiều biến thiên:
y' = 3x2 + 2x + 9 > 0
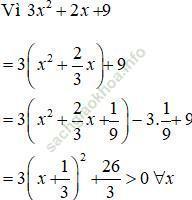
⇒ Hàm số luôn đồng biến trên R.
- Hàm số không có cực trị.
- Giới hạn:
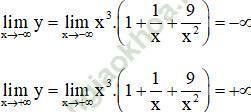
- Bảng biến thiên:
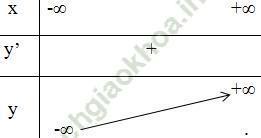
3) Đồ thị hàm số.
- Đồ thị hàm số cắt trục Ox tại (0; 0).
- Đồ thị hàm số đi qua (1; 11); (-1; -9)
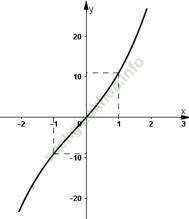
d) Hàm số y = 2x3 + 5.
1) Tập xác định: D = R
2) Sự biến thiên:
- Chiều biến thiên:
y' = 6x2 ≥ 0 ∀ x ∈ R
Hàm số đồng biến trên R
Hàm số không có cực trị.
- Giới hạn:
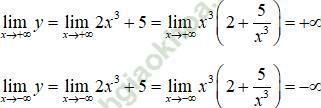
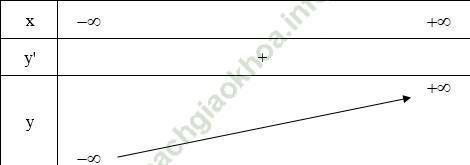
- Bảng biến thiên:
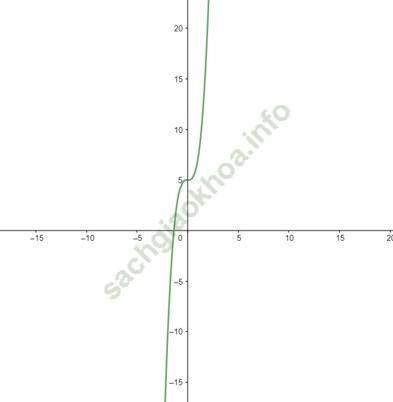
3) Vẽ đồ thị:
- Đồ thị hàm số cắt trục tung tại (0; 5)
- Đồ thị hàm số đi qua điểm (1; 7) và (-1; 3)
Bài 2 trang 43 sách giáo khoa Toán Giải tích 12
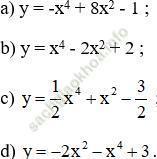
a) Hàm số y = -x4 + 8x2 – 1.
1) Tập xác định: D = R
2) Sự biến thiên:
- Chiều biến thiên:
y' = -4x3 + 16x = -4x (x2 - 4)
y' = 0 ⇔ -4x (x2 - 4) = 0 ⇔ x = 0; x = ±2
Trên khoảng (-∞; -2) và (0; 2), y’ > 0 nên hàm số đồng biến.
Trên các khoảng (-2; 0) và (2; +∞), y’ < 0 nên hàm số nghịch biến.
- Cực trị:
Hàm số đạt cực đại tại x = 2 và x = -2; yCĐ = 15
Hàm số đạt cực tiểu tại x = 0; yCT = -1.
- Giới hạn:
- Bảng biến thiên:
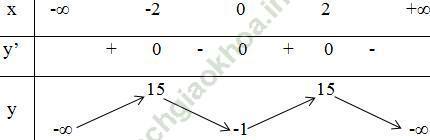
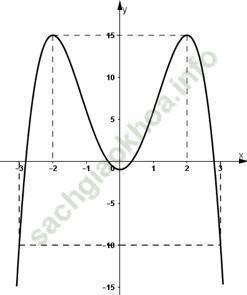
3) Vẽ đồ thị:
- Hàm số đã cho là hàm số chẵn, vì:
y (-x) = - (-x)4 + 8 (-x)2 - 1 = -x4 + 8x2 - 1 = y (x)
⇒ Đồ thị nhận Oy làm trục đối xứng.
- Giao với Oy tại điểm (0; -1) (vì y (0) = -1).
- Đồ thị hàm số đi qua (-3; -10) và (3; 10).
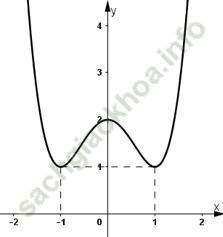
b) Hàm số y = x4 – 2x2 + 2.
1) Tập xác định: D = R
2) Sự biến thiên:
- Chiều biến thiên:
y' = 4x3 - 4x = 4x (x2 - 1)
y' = 0 ⇔ 4x (x2 - 1) = 0 ⇔ x = 0; x = ±1.
- Giới hạn:
- Bảng biến thiên:
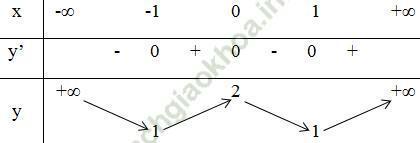
Kết luận:
- Hàm số đồng biến trên khoảng (-1; 0) và (1; +∞).
- Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1).
- Đồ thị hàm số có hai điểm cực tiểu là: (-1; 1) và (1; 1).
- Đồ thị hàm số có điểm cực đại là: (0; 2)
3) Vẽ đồ thị:
- Hàm số chẵn nên đồ thị hàm số nhận trục Oy là trục đối xứng.
- Đồ thị hàm số cắt trục tung tại (0; 2).
- Đồ thị hàm số đi qua (-1; 1) và (1; 1).
- Vẽ đồ thị hàm số:
c) Hàm số 
1) Tập xác định: D = R
2) Sự biến thiên:
- y' = 2x3 + 2x = 2x (x2 + 1)
y' = 0 ⇔ 2x (x2 + 1) = 0 ⇔ x = 0
- Giới hạn:
- Bảng biến thiên:
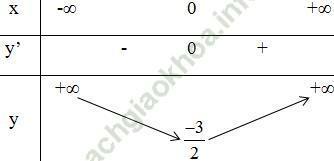
Kết luận:
- Hàm số đồng biến trên khoảng (0; +∞).
- Hàm số nghịch biến trên các khoảng (-∞; 0).
- Đồ thị hàm số có điểm cực đại là: (0; -3/2).
3) Đồ thị:
- Hàm số chẵn nên nhận trục Oy là trục đối xứng.
- Hàm số cắt trục hoành tại điểm (-1; 0) và (1; 0).
- Hàm số cắt trục tung tại điểm 
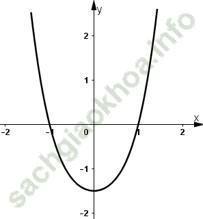
d) Hàm số y = -2x2 – x4 + 3.
1) TXĐ: D = R
2) Sự biến thiên:
- Chiều biến thiên:
y' = -4x - 4x3 = -4x (1 + x2)
y' = 0 ⇔ -4x (1 + x2) = 0 ⇔ x = 0
- Giới hạn:
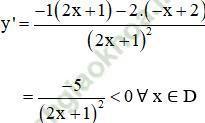
- Bảng biến thiên:
Kết luận:
- Hàm số đồng biến trên khoảng (-∞; 0).
- Hàm số nghịch biến trên các khoảng (0; +∞).
- Đồ thị hàm số có điểm cực đại là: (0; 3).
3) vẽ đồ thị:
- Hàm số là hàm số chẵn nên nhận trục Oy là trục đối xứng.
- Hàm số cắt trục Ox tại (-1; 0) và (1; 0).
- Hàm số cắt trục Oy tại (0; 3).
Bài 3 trang 43 sách giáo khoa Toán Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị các hàm số phân thức:
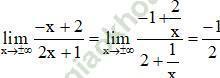
Lời giải:
a) Hàm số 
1) TXĐ: D = R \ {1}
2) Sự biến thiên:
- Chiều biến thiên:
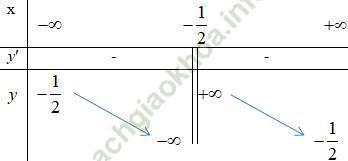
Suy ra, Hàm số nghịch biến trên (-∞; 1) và (1; +∞).
- Cực trị: Hàm số không có cực trị.
- Tiệm cận:
Suy ra, x = 1 là tiệm cận đứng.
Lại có:
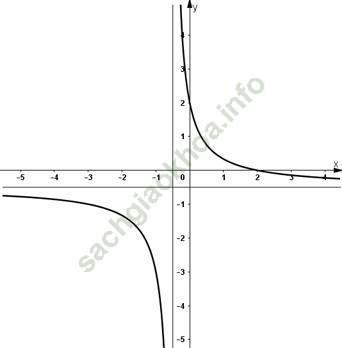
Suy ra, y = 1 là tiệm cận ngang.
- Bảng biến thiên:
3) Vẽ đồ thị:
- Giao với Oy: (0; -3)
- Giao với Ox: (-3; 0)
- Đồ thị nhận (1; 1) là tâm đối xứng.
b) Hàm số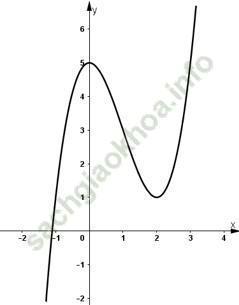 
1) Tập xác định: D = R \ {2}
2) Sự biến thiên:
- Chiều biến thiên:
Suy ra, Hàm số đồng biến trên (-∞; 2) và (2; +∞).
- Cực trị: Hàm số không có cực trị.
- Tiệm cận:
Suy ra, x = 2 là tiệm cận đứng của đồ thị hàm số.
Lại có:
Suy ra, y = -1 là tiệm cận ngang.
- Bảng biến thiên:
3) Vẽ đồ thị:
- Giao với Oy: (0; -1/4)
- Giao với Ox: (1/2; 0)
- Đồ thị hàm số nhận (2; -1) là tâm đối xứng.
c) Hàm số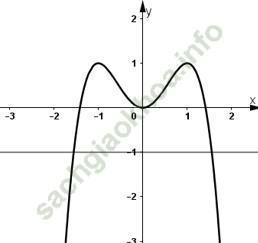 
1) Tập xác định: D = R \ {-1/2}
2) Sự biến thiên:
- Chiều biến thiên:
Suy ra, Hàm số nghịch biến trên (-∞; -1/2) và (-1/2; +∞).
- Cực trị: Hàm số không có cực trị.
- Tiệm cận:
Suy ra,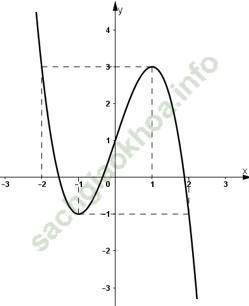 
là tiệm cận đứng của đồ thị hàm số.
Suy ra, 
là tiệm cận ngang.
- Bảng biến thiên:
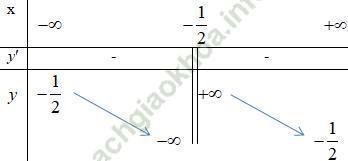
3) Vẽ đồ thị:
- Giao với Oy: (0; 2)
- Giao với Ox: (2; 0)
- Đồ thị hàm số nhận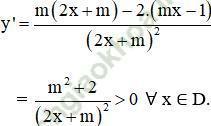 
là tâm đối xứng.
Bài 4 trang 44 sách giáo khoa Toán Giải tích 12
Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:
a) x3 - 3x2 + 5 = 0;
b) -2x3 + 3x2 - 2 = 0;
c) 2x2 - x4 = -1
Kiến thức áp dụng
Số nghiệm của phương trình f (x) = m phụ thuộc vào số giao điểm của đồ thị hàm số y = f (x) và đường thẳng y = m.
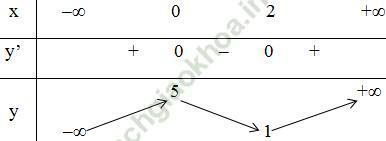
a) Xét y = f (x) = x3 - 3x2 + 5 (1)
- Tập xác định: D = R
- Sự biến thiên:
+ Chiều biến thiên:
f' (x) = 3x2 - 6x = 3x (x - 2)
f' (x) = 0 ⇔ x = 0; x = 2
+ Giới hạn:
+ Bảng biến thiên:
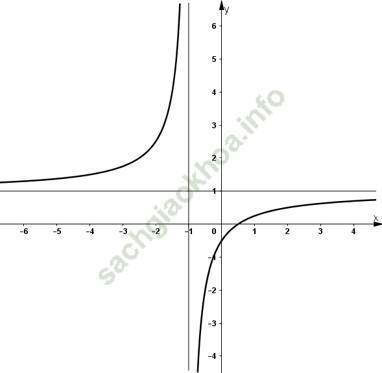
- Vẽ đồ thị:
Đồ thị hàm số y = f (x) cắt trục hoành tại 1 điểm duy nhất.
Suy ra, phương trình x3 - 3x2 + 5 = 0 chỉ có 1 nghiệm duy nhất.
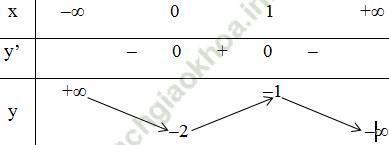
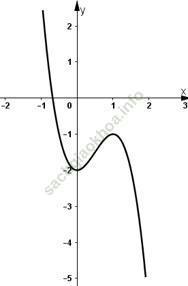
b) Xét hàm số y = f (x) = -2x3 + 3x2 – 2.
- Tập xác định: D = R
- Sự biến thiên:
+ Chiều biến thiên:
y' = -6x2 + 6x = -6x (x - 1)
y' = 0 ⇔ x = 0; x = 1
+ Giới hạn:
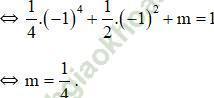
+ Bảng biến thiên:
- Vẽ đồ thị:
Đồ thị hàm số y = f (x) cắt trục hoành tại 1 điểm duy nhất
Suy ra, phương trình f (x) = 0 có nghiệm duy nhất.
Vậy phương trình -2x3 + 3x2 - 2 = 0 chỉ có một nghiệm.
c) Xét hàm số y = f (x) = 2x2 - x4
- Tập xác định: D = R
- Sự biến thiên:
+ Chiều biến thiên:
y' = 4x - 4x3 = 4x (1 - x2)
y' = 0 ⇔ x = 0; x = ±1
+ Giới hạn:
- Số nghiệm của phương trình f (x) = m phụ thuộc vào số giao điểm của đồ thị hàm số y = f (x) và đường thẳng y = m.
+ Bảng biến thiên:
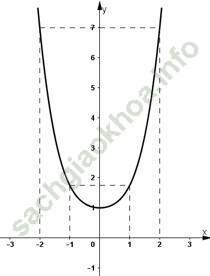
- Vẽ đồ thị:
Đồ thị hàm số y = f (x) cắt đường thẳng y = -1 tại hai điểm
Suy ra, Phương trình f (x) = -2 có hai nghiệm phân biệt.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
y = -x3 + 3x + 1
b) Dựa vào đồ thị (C), biện luận về số nghiệm của phương trình sau theo tham số m:
x3 - 3x + m = 0
Lời giải:a) Khảo sát hàm số y = -x3 + 3x + 1
- Tập xác định: D = R
- Sự biến thiên:
+ Chiều biến thiên:
y' = -3x2 + 3 = -3 (x2 - 1)
y' = 0 ⇔ -3 (x2 - 1) = 0 ⇔ x = ±1.
+ Giới hạn:
+ Bảng biến thiên:
Kết luận:
Hàm số đồng biến trên khoảng (-1; 1).
Hàm số nghịch biến trên các khoảng (-∞; -1) và (1; +∞).
Hàm số đạt cực tiểu tại x = -1; yCT = -1.
Hàm số đạt cực đại tại x = 1; yCĐ = 3.
- Vẽ đồ thị:
+ Giao với Oy: (0; 1).
+ Đồ thị (C) đi qua điểm (-2; 3), (2; -1).
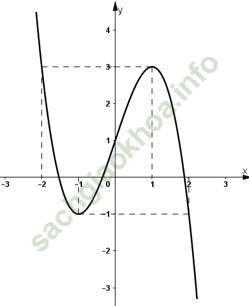
b) Ta có: x3 - 3x + m = 0 (*)
⇔ -x3 + 3x + 1 = m + 1
Số nghiệm của phương trình (*) phụ thuộc số giao điểm của đồ thị hàm số y = -x3 + 3x + 1 và đường thẳng y = m + 1.
Kết hợp với quan sát đồ thị hàm số ta có:
- Nếu m + 1 < –1 ⇔ m < –2
⇒ (C) cắt (d) tại 1 điểm.
Suy ra, phương trình (*) có 1 nghiệm.
- Nếu m + 1 = –1 ⇔ m = –2
⇒ (C) cắt (d) tại 2 điểm
Suy ra, phương trình (*) có 2 nghiệm.
- Nếu –1 < m + 1 < 3 ⇔ –2 < m < 2
⇒ (C) cắt (d) tại 3 điểm.
Suy ra, phương trình (*) có 3 nghiệm.
- Nếu m + 1 = 3 ⇔ m = 2
⇒ (C) cắt (d) tại 2 điểm.
Suy ra, phương trình (*) có hai nghiệm.
- Nếu m + 1 > 3 ⇔ m > 2
⇒ (C) cắt (d) tại 1 điểm
Suy ra, phương trình (*) có một nghiệm.
Kết luận: + Với m < -2 hoặc m > 2 thì phương trình có 1 nghiệm.
- Với m = -2 hoặc m = 2 thì phương trình có 2 nghiệm.
- Với -2 < m < 2 thì phương trình có 3 nghiệm.
Bài 6 trang 44 sách giáo khoa Toán Giải tích 12
a) Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên khoảng xác định của nó.
b) Xác định m để tiệm cận đứng của đồ thị đi qua A (-1, √2).
c) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 2.
+ Hàm số y = f (x) có đạo hàm trên khoảng K xác định thì:
f (x) đồng biến nếu f’ (x) > 0 với ∀ x ∈ K.
+ Đường thẳng x = x0 là tiệm cận đứng của đồ thị hàm số y = f (x) nếu có
a) Với mọi tham số m ta có:
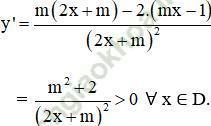
Vậy hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Ta có:
Suy ra, 
là tiệm cận đứng của đồ thị hàm số.
- Vẽ đồ thị:
+ Đồ thị cắt trục hoành tại (1/2; 0).
+ Đồ thị cắt trục tung tại (0; -1/2).
+ Đồ thị nhận I (-1; 1) là tâm đối xứng.
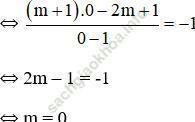
Bài 7 trang 44 sách giáo khoa Toán 12 Giải tích
Câu hỏi:Cho hàm số
a) Với giá trị nào của tham số m, đồ thị của hàm đi qua điểm (-1; 1)?
b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.
c) Viết phương trình tiếp tuyến (C) tại điểm có tung độ bằng 7/4.
Lời giải:a) Đồ thị hàm số qua điểm (-1; 1)
b) Với m = 1, hàm số trở thành 
- TXĐ: D = R
- Sự biến thiên:
+ Chiều biến thiên:
y' = x3 + x = x (x2 + 1)
y' = 0 ⇔ x (x2 + 1) ⇔ x = 0
+ Giới hạn:
+ Bảng biến thiên:
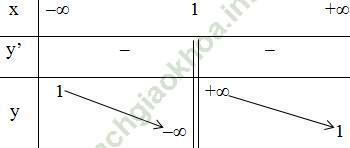
Kết luận:
Hàm số đồng biến trên (0; +∞)
Hàm số nghịch biến trên (-∞; 0)
Hàm số có điểm cực tiểu là (0; 1).
- Vẽ đồ thị:
+ Đồ thị nhận trục Oy là trục đối xứng.
+ Đồ thị cắt trục tung tại (0; 1).
+ Đồ thị hàm số đi qua (-1; 1,75); (1; 1,75); (-2; 7); (2; 7).
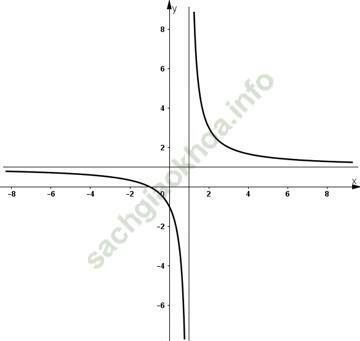
c) Điểm thuộc (C) có tung độ bằng 7/4 nên hoành độ của điểm đó là nghiệm của phương trình:
+ Phương trình tiếp tuyến của (C) tại 
:
y’ (1) = 2
Suy ra, Phương trình tiếp tuyến: 
hay 
+ Phương trình tiếp tuyến của (C) tại 
:
y’ (-1) = -2.
Suy ra, phương trình tiếp tuyến: 
hay y = 
Bài 8 trang 44 sách giáo khoa Toán 12 Giải tích
Cho hàm số:
y = x3 + (m + 3)x2 + 1 - m (m là tham số) có đồ thị (Cm).
a) Xác định m để hàm số có điểm cực đại là x = -1.
b) Xác định m để đồ thị (Cm) cắt trục hoành tại x = -2.
Kiến thức áp dụng
+ Hàm số y = f (x) có đạo hàm cấp hai trong khoảng K, khi đó, với y0 ∈ K ta có:
Nếu f’ (y0) = 0 và f’’ (y0) < 0 thì y0 là điểm cực đại.
a) Xét hàm số y = x3 + (m + 3)x2 + 1 – m.
+ TXĐ: D = R.
+ y’ = 3x2 + 2 (m + 3).x
Suy ra, y’’ = 6x + 2 (m + 3).
+ Hàm số có điểm cực đại là x = -1
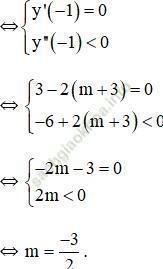
Vậy với 
thì hàm số có điểm cực đại là x = -1.
b) Đồ thị (Cm) cắt trục hoành tại x = -2
⇔ y (-2) = 0
⇔ (-2)3 + (m + 3)(-2)2 + 1 - m = 0
⇔ -8 + 4 (m + 3) + 1 - m = 0
⇔ 3m + 5 = 0
⇔ m = -5/3
Cho hàm số 
(m là tham số) có đồ thị (G).
a) Xác định m để đồ thị (G) đi qua điểm (0; -1).
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m tìm được.
c) Viết phương trình tiếp tuyến của đồ thị trên tại giao điểm của nó với trục tung.
Lời giải:a) Đồ thị (G) đi qua điểm (0; -1)
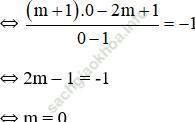
b) Với m = 0, hàm số trở thành: 
- TXĐ: D = R \ {1}
- Sự biến thiên:
+ Chiều biến thiên:
Suy ra, Hàm số nghịch biến trên (-∞; 1) và (1; +∞).
+ Cực trị: Hàm số không có cực trị.
+ Tiệm cận:
⇒ x = 1 là tiệm cận đứng của đồ thị hàm số.
⇒ y = 1 là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên:
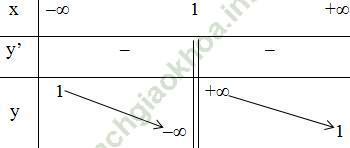
- Vẽ đồ thị:
+ Giao điểm với Ox: (-1; 0)
+ Giao điểm với Oy: (0; -1)
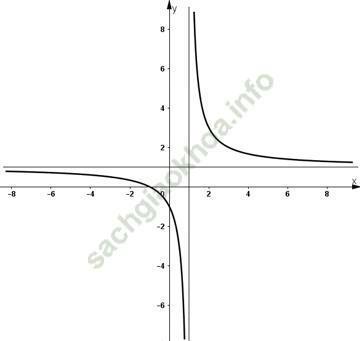
c) Đồ thị cắt trục tung tại điểm P (0; -1), khi đó phương trình tiếp tuyến tại điểm P (0; -1) là:
y = y' (0). (x - 0) - 1 hay y = -2x - 1
Vậy phương trình tiếp tuyến cần tìm là: y = -2x – 1.