Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Giải BT Toán 12
Trả lời câu hỏi Toán 12 Giải tích Bài 3 trang 20: Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = (x + 1)/ (x - 1) trên đoạn [3; 5].
Bài giải:a) y’ = 2x ≤ 0 trên đoạn [-3; 0]. Vậy hàm số nghịch biến trên đoạn [-3,0].
Khi đó trên đoạn [-3,0]: hàm số đạt giá trị lớn nhất tại x = -3 và giá trị lớn nhất bằng 9, hàm số đạt giá trị nhỏ nhất tại x = 0 và giá trị nhỏ nhất = 0.
b) y’ = (-2)/ (x-1)2 < 0 trên đoạn [3; 5]. Vậy hàm số nghịch biến trên đoạn [3; 5].
Khi đó trên đoạn [-3,5]: hàm số đạt giá trị lớn nhất tại x = 3 và giá trị lớn nhất bằng 2, hàm số đạt giá trị nhỏ nhất tại x = 5 và giá trị nhỏ nhất = 1.5.
Trả lời câu hỏi Toán 12 Giải tích Bài 3 trang 21:
Cho hàm số
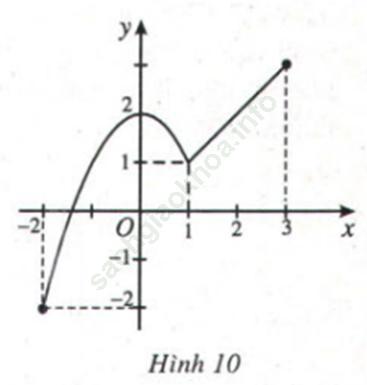
Có đồ thị như Hình 10. Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2; 3] và nêu cách tính.
Bài giải:Giá trị nhỏ nhất của hàm số trên đoạn [-2,3] là điểm thấp nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị nhỏ nhất tại x = -2. Thay x = -2 vào hàm số y đã cho ta có giá trị nhỏ nhất là -2.
Giá trị lớn nhất của hàm số trên đoạn [-2,3] là điểm cao nhất của đồ thị trên đoạn đó. Vậy hàm số đạt giá trị lớn nhất tại x = 3. Thay x = 3 vào hàm số y đã cho ta có giá trị lớn nhất là 3.

Trả lời câu hỏi Toán 12 Giải tích Bài 3 trang 23: Lập bảng biến thiên của hàm số f (x) = (-1)/ (1 + x2).
Từ đó suy ra giá trị nhỏ nhất của f (x) trên tập xác định.
Bài giải:1. TXĐ: D = R.
2. y’ = 2x/ (1 + x2)2. Cho y’ = 0 thì x = 0.
3. Bảng biến thiên:
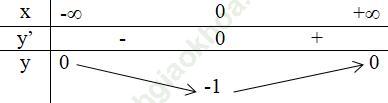
Vậy giá trị nhỏ nhất của hàm số đã cho là – 1 tại x = 0.
Giải bài 1 trang 23 sgk Giải tích 12
Kiến thức áp dụngQuy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f (x) trên [a; b].
+ Tìm các điểm xi trên khoảng (a; b) sao cho tại đó f’ (xi) = 0 hoặc không xác định.
+ Tính f (a); f (xi); f (b).
+ Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
Nếu hàm số đồng biến trên [a; b] thì
Nếu hàm số nghịch biến trên [a; b] thì
Giải bài 2 trang 24 sgk Giải tích 12
Kiến thức áp dụng+ Số M được gọi là giá trị lớn nhất của hàm số y = f (x) trên tập D nếu f (x) ≤ M với mọi x thuộc D và tồn tại x0 ∈ D để f (x0) = M.
Giải bài 3 trang 24 sgk Giải tích 12
Kiến thức áp dụng+ Số M được gọi là giá trị lớn nhất của hàm số y = f (x) trên tập D nếu f (x) ≤ M với mọi x thuộc D và tồn tại x0 ∈ D để f (x0) = M.
Giải bài 4 trang 24 sgk Giải tích 12
Kiến thức áp dụng+ Số M được gọi là giá trị lớn nhất của hàm số y = f (x) trên tập D nếu f (x) ≤ M với mọi x thuộc D và tồn tại x0 ∈ D để f (x0) = M.
Giải bài 5 trang 24 sgk Giải tích 12
Kiến thức áp dụng+ Số M được gọi là giá trị lớn nhất của hàm số y = f (x) trên tập D nếu f (x) ≤ M với mọi x thuộc D và tồn tại x0 ∈ D để f (x0) = M.