Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp (Toán 8 Bài 9)
Câu hỏi Toán 8 Tập 1 Bài 9 trang 23: Thực hiện phân tích đa thức: 2x3y – 2xy3 – 4xy2 – 2xy thành nhân tử.
Lời giải
2x3y – 2xy3 – 4xy2 – 2xy
= 2xy (x2 - y2 - 2y - 1)
= 2xy [x2 - (y2 + 2y + 1)]
= 2xy [x2 - (y + 1)2]
= 2xy (x + y + 1)(x - y - 1)
Câu hỏi Toán 8 Tập 1 Bài 9 trang 23:
a. Tính nhanh biểu thức: x2 + 2x + 1 - y2 với x = 94,5 và y = 4,5.
b. Phân tích đa thức x2 + 4x – 2xy – 4y + y2 thành nhân tử; bạn Vinh làm như sau:
x2 + 4x – 2xy – 4y + y2
= (x2 - 2xy + y2) + (4x – 4y)
= (x - y)2 + 4 (x – y)
= (x – y)(x – y + 4).
Em hãy cho biết trong cách làm bài ở trên, bạn Vinh đã sử dụng phương pháp nào để phân tích đa thức thành nhân tử.
Lời giải
a. x2 + 2x + 1 - y2
= (x + 1)2-y2
= (x + y + 1)(x - y + 1)
Thay tại x = 94,5 và y = 4,5 ta được:
(x + y + 1)(x - y + 1)
= (94,5 + 4,5 + 1)(94,5 - 4,5 + 1)
= 100.91
= 9100
b. x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) => bạn Vinh đã dùng phương pháp nhóm hạng tử
= (x - y)2 + 4 (x – y) => bạn Vinh đã dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) => bạn Vinh đã dùng phương pháp đặt nhân tử chung
Câu hỏi Toán 8 Tập 1 Bài 9 trang 24:
Hãy chứng minh rằng: (5n + 2)2 – 4 chia hết cho 5 với mọi số nguyên n.
Lời giải:
Ta có: (5n + 2)2 – 4
= (5n + 2)2 – 22
= (5n + 2 – 2)(5n + 2 + 2)
= 5n (5n + 4)
Vì 5 ⋮ 5 nên 5n (5n + 4) ⋮ 5 ∀ n ∈ Ζ.
Vậy (5n + 2)2 – 4 luôn chia hết cho 5 với n ∈ Ζ
Câu hỏi Toán 8 Tập 1 Bài 9 trang 24: Thực hiện phân tích những đa thức sau thành nhân tử:
a. x2 – 3x + 2
b. x2 + x – 6
c. x2 + 5x + 6
Lời giải:Cách 1: Tách một hạng tử thành tổng 2 hạng tử để xuất hiện nhân tử chung.
x2 – 3x + 2
= x2 – x – 2x + 2 (Tách –3x = – x – 2x)
= (x2 – x) – (2x – 2)
= x (x – 1) – 2 (x – 1) (Có x – 1 là nhân tử chung)
= (x – 1)(x – 2)
Hoặc: x2 – 3x + 2
= x2 – 3x – 4 + 6 (Tách 2 = – 4 + 6)
= x2 – 4 – 3x + 6
= (x2 – 22) – 3 (x – 2)
= (x – 2)(x + 2) – 3. (x – 2) (Xuất hiện nhân tử chung x – 2)
= (x – 2)(x + 2 – 3)
= (x – 2)(x – 1)
b. x2 + x – 6
= x2 + 3x – 2x – 6 (Tách x = 3x – 2x)
= x (x + 3) – 2 (x + 3) (có x + 3 là nhân tử chung)
= (x + 3)(x – 2)
c. x2 + 5x + 6 (Tách 5x = 2x + 3x)
= x2 + 2x + 3x + 6
= x (x + 2) + 3 (x + 2) (Có x + 2 là nhân tử chung)
= (x + 2)(x + 3)
Cách 2: Đưa về các hằng đẳng thức 1 hoặc 2:
a. x2 – 3x + 2
(Vì có x2 và
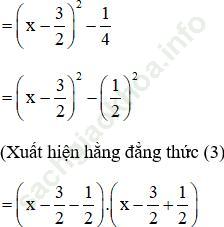
= (x – 2)(x – 1)
b. x2 + x - 6

= (x – 2)(x + 3).
c. x2 + 5x + 6

= (x + 2)(x + 3).
Câu hỏi Toán 8 Tập 1Bài 9 trang 25: Thực hiện phân tích những đa thức sau thành nhân tử:
a. x3 + 2x2y + xy2 – 9x
b. 2x – 2y – x2 + 2xy – y2
c. x4 – 2x2
Lời giải:a. x3 + 2x2y + xy2 – 9x (Có x là nhân tử chung)
= x (x2 + 2xy + y2 – 9) (Có x2 + 2xy + y2 là hằng đẳng thức)
= x [(x2 + 2xy + y2) – 9]
= x [(x + y)2 – 32] (Xuất hiện hằng đẳng thức 3]
= x (x + y – 3)(x + y + 3)
b. 2x – 2y – x2 + 2xy – y2
(Có x2; 2xy; y2 ta nhớ đến hằng đẳng thức 1 hoặc 2)
= (2x – 2y) – (x2 – 2xy + y2)
= 2 (x – y) – (x – y)2 (Có x – y là nhân tử chung)
= (x – y)[2 – (x – y)]
= (x – y)(2 – x + y)
c. x4 – 2x2
(Có x2 là nhân tử chung)
= x2(x2 – 2)
Câu hỏiToán 8 Tập 1Bài 9 trang 25: Tìm x, biết:
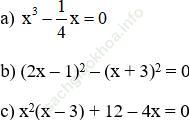
Đáp án:
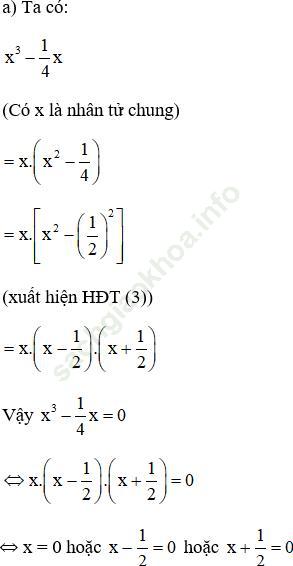
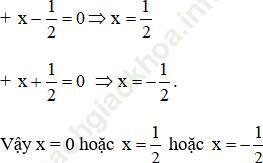
b. Ta có: (2x – 1)2 – (x + 3)2 (xuất hiện hằng đẳng thức 3)
= [(2x – 1) – (x + 3)] [(2x – 1) + (x + 3)]
= (2x – 1 – x – 3). (2x – 1 + x + 3)
= (x – 4)(3x + 2)
Vậy (2x – 1)2 – (x + 3)2 = 0
⇔ (x – 4)(3x + 2) = 0
⇔ x – 4 = 0 hoặc 3x + 2 = 0
⇔ x = 4 hoặc x = –2/3
Vậy x = 4 hoặc x = –2/3.
c. Ta có: x2(x – 3) + 12 – 4x
= x2(x – 3) – 4. (x – 3) (Có nhân tử chung là x – 3)
= (x2 – 4)(x – 3)
= (x2 – 22). (x – 3) (Xuất hiện HĐT (3))
= (x – 2)(x + 2)(x – 3)
Vậy x2(x – 3) + 12 – 4x = 0
⇔ (x – 2)(x + 2)(x – 3) = 0
⇔ x – 2 = 0 hoặc x + 2 = 0 hoặc x – 3 = 0
⇔ x = 2 hoặc x = –2 hoặc x = 3.
Vậy x = 2 hoặc x = –2 hoặc x = 3.