Luyện tập ( Toán 8 LT)

Câu hỏi Toán 8 Tập 1trang 25: Thực hiện phân tích những đa thức sau thành nhân tử:

a. x³ + 2x²y + xy² – 9x

b. 2x – 2y – x² + 2xy – y²

c. x⁴ – 2x²

Lời giải:

a. x³ + 2x²y + xy² – 9x (Có x là nhân tử chung)

= x (x² + 2xy + y² – 9) (Có x² + 2xy + y² là hằng đẳng thức)

= x [(x² + 2xy + y²) – 9]

= x [(x + y)² – 3²] (Xuất hiện hằng đẳng thức 3)

= x (x + y – 3)(x + y + 3)

b. 2x – 2y – x² + 2xy – y²

(Có x²; 2xy; y² ta nhớ đến hằng đẳng thức 1 hoặc 2)

= (2x – 2y) – (x² – 2xy + y²)

= 2 (x – y) – (x – y)² (Có x – y là nhân tử chung)

= (x – y)[2 – (x – y)]

= (x – y)(2 – x + y)

c. x⁴ – 2x² (Có x² là nhân tử chung)

= x²(x² – 2)

Câu hỏi Toán 8 Tập 1 trang 25: Tìm x với các biểu thức dưới đây, biết:

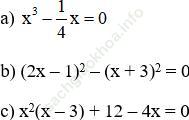
Đáp án:

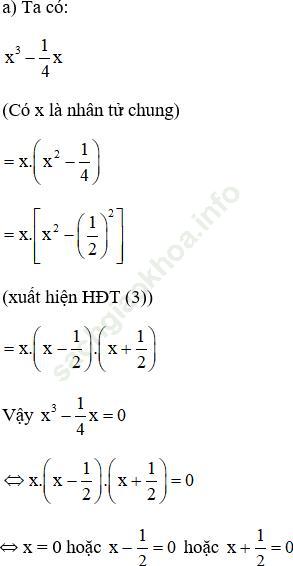
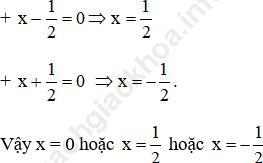
b. Ta có: (2x – 1)² – (x + 3)² (xuất hiện hằng đẳng thức 3)

= [(2x – 1) – (x + 3)] [(2x – 1) + (x + 3)]

= (2x – 1 – x – 3). (2x – 1 + x + 3)

= (x – 4)(3x + 2)

Vậy (2x – 1)² – (x + 3)² = 0

⇔ (x – 4)(3x + 2) = 0

⇔ x – 4 = 0 hoặc 3x + 2 = 0

⇔ x = 4 hoặc x = –2/3

Vậy x = 4 hoặc x = –2/3.

c. Ta có: x²(x – 3) + 12 – 4x

= x²(x – 3) – 4. (x – 3) (Có nhân tử chung là x – 3)

= (x² – 4)(x – 3)

= (x² – 2²). (x – 3) (Xuất hiện hằng đẳng thức 3)

= (x – 2)(x + 2)(x – 3)

Vậy x²(x – 3) + 12 – 4x = 0

⇔ (x – 2)(x + 2)(x – 3) = 0

⇔ x – 2 = 0 hoặc x + 2 = 0 hoặc x – 3 = 0

⇔ x = 2 hoặc x = –2 hoặc x = 3.

Vậy x = 2 hoặc x = –2 hoặc x = 3.

Câu hỏi Toán 8 Tập 1trang 25: Tính nhanh giá trị của các đa thức sau đây:

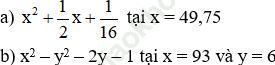
Đáp án:

a. Ta có:

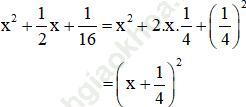
Do vậy, với x = 49,75, giá trị biểu thức bằng

b. Ta có:

x² – y² – 2y – 1 (Thấy có y²; 2y; 1 ta liên tưởng đến HĐT (1) hoặc (2))

= x² – (y² + 2y + 1)

= x² – (y + 1)² (Xuất hiện HĐT (3))

= (x – y – 1)(x + y + 1)

Tại x = 93, y = 6 thì:

(93 – 6 – 1)(93 + 6 + 1)

= 86.100 = 8600

Câu hỏi Toán 8 Tập 1 trang 25: Thực hiện phân tích những đa thức sau thành nhân tử:

a. x² – 4x + 3

b. x² + 5x + 4

c. x² – x – 6;

d. x⁴ + 4

Lời giải:

a) Cách 1: x² – 4x + 3

= x² – x – 3x + 3

* Tách –4x = –x – 3x)

= x (x – 1) – 3 (x – 1) (Có x – 1 là nhân tử chung)

= (x – 1)(x – 3)

Cách 2: x² – 4x + 3

= x² – 2. x. 2 + 2² + 3 – 2²

* Thêm bớt 2² để có hằng đẳng thức 2:

= (x – 2)² – 1 (Xuất hiện hằng đẳng thức 3)

= (x – 2 – 1)(x – 2 + 1)

= (x – 3)(x – 1)

b. x² + 5x + 4

= x² + x + 4x + 4

* Tách 5x = x + 4x

= x (x + 1) + 4 (x + 1) (có x + 1 là nhân tử chung)

= (x + 1)(x + 4)

c. x² – x – 6

= x² + 2x – 3x – 6

* Tách –x = 2x – 3x

= x (x + 2) – 3 (x + 2) (có x + 2 là nhân tử chung)

= (x – 3)(x + 2)

d. x⁴ + 4

= (x²)² + 2²

= x⁴ + 2. x².2 + 4 – 4x²

* Thêm bớt 2. x².2 để có hằng đẳng thức 1

= (x² + 2)² – (2x)² (Xuất hiện hằng đẳng thức 3)

= (x² + 2 – 2x)(x² + 2 + 2x)

Câu hỏi Toán 8 Tập 1 trang 25: Hãy chứng minh rằng n³ – n chia hết cho 6 với mọi số nguyên n.

Lời giải:

A = n³ – n (có nhân tử chung n)

= n (n² – 1) (Xuất hiện hằng đẳng thức 3)

= n (n – 1)(n + 1)

Vì: n – 1; n và n + 1 là ba số tự nhiên liên tiếp nên

- Trong đó có ít nhất một số chẵn => (n – 1).n. (n + 1) ⋮ 2

- Trong đó có ít nhất một số chia hết cho 3 => (n – 1).n. (n + 1) ⋮ 3

Vậy A ⋮ 2 và A ⋮ 3 nên A ⋮ 6.

Bài trước: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp (Toán 8 Bài 9) Bài tiếp: Chia đơn thức cho đơn thức (Toán 8 Bài 10)